Что такое диаграмма в математике
Содержимое
- 1 Что такое диаграмма в математике
- 1.1 Диаграмма в математике
- 1.2 Основные понятия
- 1.3 Способы представления данных
- 1.4 Столбчатая диаграмма
- 1.5 Круговая диаграмма
- 1.6 Линейная диаграмма
- 1.7 Гистограмма
- 1.8 Вопрос-ответ:
- 1.8.0.1 Что такое диаграмма в математике?
- 1.8.0.2 Какие основные понятия связаны с диаграммой в математике?
- 1.8.0.3 Какие способы представления данных с помощью диаграмм существуют?
- 1.8.0.4 Какие преимущества использования диаграмм в математике?
- 1.8.0.5 Какие недостатки могут быть у диаграмм в математике?
- 1.8.0.6 Какие основные понятия связаны с диаграммами в математике?
- 1.9 Видео по теме:
Диаграмма в математике представляет собой визуальное представление данных или отношений между ними с использованием графических элементов, таких как точки, линии и круги. Она помогает увидеть закономерности, тренды и связи в данных, что позволяет анализировать и прогнозировать различные явления и процессы.
Диаграмма – это графическое представление данных, которое позволяет наглядно и наглядно исследовать зависимости между различными величинами. В математике, диаграммы используются для визуализации математических концепций и представления данных. Они помогают нам лучше понять отношения между различными параметрами и сделать выводы на основе собранных данных.
Основными типами диаграмм являются столбчатые, круговые, линейные и точечные диаграммы. Столбчатая диаграмма отображает данные с использованием столбцов различной высоты, где каждый столбец соответствует определенной категории. Круговая диаграмма представляет данные в виде круга, разделенного на секторы, пропорциональные величине соответствующих категорий. Линейная диаграмма показывает изменение величины одной переменной относительно другой, используя линию. Точечная диаграмма позволяет нам исследовать взаимосвязь между двумя переменными, где каждая точка представляет собой пару значений.
Диаграммы упрощают анализ данных, позволяя нам увидеть общую картину и выявить закономерности. Они помогают нам делать выводы на основе собранных данных и принимать обоснованные решения. Наглядное представление данных в виде диаграмм позволяет нам лучше понять более абстрактные математические концепции и улучшить наши навыки визуализации и интерпретации информации.
Все диаграммы имеют общие элементы: оси, метки, заголовки и легенды. Оси используются для отображения значений и масштабирования данных. Метки помогают нам идентифицировать значения на осях и категории данных. Заголовки дают общую информацию о диаграмме, а легенда объясняет, что представляет каждый столбец или сектор. Все эти элементы делают диаграммы более понятными и позволяют нам извлекать максимум информации из представленных данных.
Диаграмма в математике
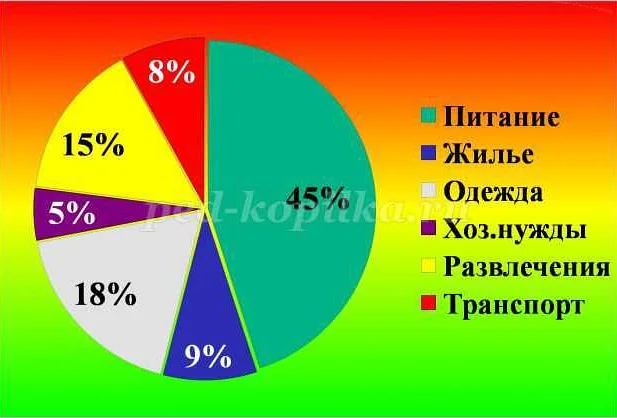
Основное назначение диаграммы – отображение информации в виде графического изображения, которое позволяет сравнивать и анализировать данные. Диаграмма может быть использована для представления числовых значений, процентного соотношения, временных интервалов, а также для отображения отношений и сравнения различных элементов.
Существует несколько основных видов диаграмм, которые широко используются в математике:
- Линейная диаграмма. Отображает изменение значений во времени или другой непрерывной шкале.
- Столбчатая диаграмма. Используется для сравнения количественных значений разных категорий.
- Круговая диаграмма. Показывает соотношение долей или процентное соотношение элементов в целом.
- Гистограмма. Используется для представления данных в виде столбцов, где высота столбца соответствует количественному значению.
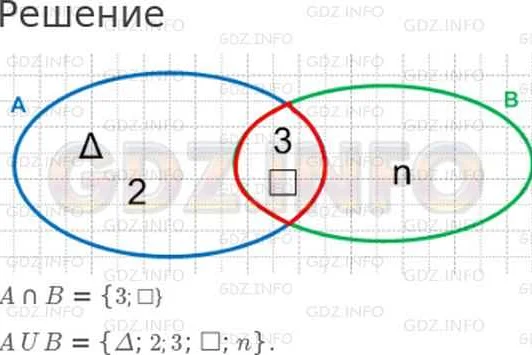
- Точечная диаграмма. Показывает взаимосвязь между двумя переменными и образует область распределения значений.
Каждый из этих видов диаграмм имеет свои особенности и применяется в зависимости от целей и характера представляемых данных. Важно уметь правильно выбирать и использовать диаграмму для наглядной и точной передачи информации.
Основные понятия
Диаграмма в математике представляет собой графическое изображение данных или информации, которое помогает наглядно представить и анализировать различные математические концепции и связи между ними.
Одно из основных понятий, связанных с диаграммами, — это «оси». Оси являются горизонтальными и вертикальными линиями на диаграмме, которые используются для измерения и отображения значений величин. Горизонтальная ось называется «ось абсцисс», а вертикальная ось — «ось ординат». Оси помогают определить масштаб и соотношения между значениями на диаграмме.
Другим важным понятием является «значения». Значения представляют собой числовые данные, которые отображаются на диаграмме. Они могут быть дискретными (отдельными точками или категориями) или непрерывными (непрерывным спектром значений). Значения представляют собой основу для построения диаграммы и помогают в анализе данных.
Диаграммы включают различные типы графиков и диаграмм, такие как столбчатые диаграммы, круговые диаграммы, линейные графики и т. д. Каждый тип диаграммы имеет свои особенности и предназначение для определенного типа данных или задачи.
Диаграммы могут использоваться для визуализации данных, сравнения значений, анализа трендов и отображения отношений между различными переменными. Они позволяют легче воспринимать информацию и делать выводы на основе визуального представления данных.
В итоге, понимание основных понятий, связанных с диаграммами, позволяет использовать их эффективно в математическом анализе и представлении данных.
Способы представления данных
Существует несколько способов представления данных на диаграммах:
СпособОписание
| Линейная диаграмма | Представление данных на графике в виде линий, соединяющих точки с координатами, соответствующими значениям переменных. |
| Столбчатая диаграмма | Представление данных на графике в виде параллельных столбцов, высота которых соответствует значениям переменных. |
| Круговая диаграмма | Представление данных на графике в виде секторов круга, площадь которых соответствует значениям переменных. |
| Площадная диаграмма | Представление данных на графике в виде фигур, площадь которых соответствует значениям переменных. |
Каждый из этих способов имеет свои преимущества и недостатки, и выбор конкретного способа зависит от характера данных, которые нужно представить.
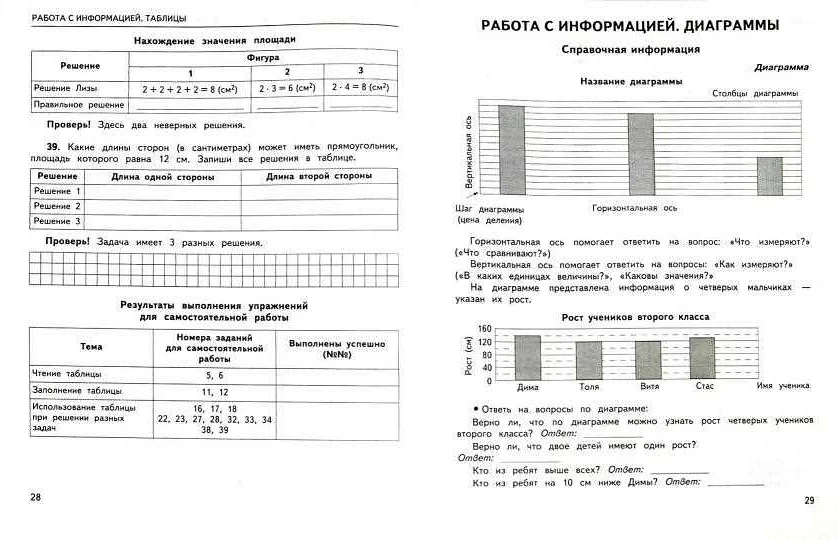
Столбчатая диаграмма
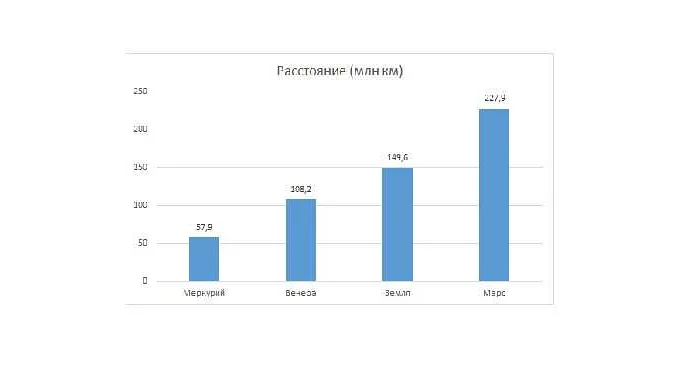
Столбцы диаграммы строятся на основе числовых данных, которые размещаются вдоль одной из осей диаграммы. Часто на горизонтальной оси отображаются категории или наборы данных, а на вертикальной оси откладывается числовая шкала, отражающая величину данных.
Столбцы диаграммы могут быть разного цвета или штриховки, чтобы визуально отличать различные категории данных. Высота каждого столбца соответствует величине данных, которые он представляет. Таким образом, столбчатая диаграмма позволяет сравнивать значения разных категорий или наборов данных.
Столбчатые диаграммы могут быть использованы для анализа различных параметров, таких как объем продаж, количество посетителей, уровень доходов и многое другое. Они позволяют наглядно представить данные и обнаружить закономерности, тренды или аномалии.
Для построения столбчатой диаграммы необходимо собрать и организовать данные, выбрать соответствующую шкалу и оси, и отобразить данные в виде столбцов. Для улучшения наглядности можно добавить подписи к осям, легенду и другие элементы диаграммы.
Столбчатые диаграммы могут быть использованы в различных областях, например, в экономике, статистике, бизнесе и науке. Они являются эффективным инструментом для визуализации и анализа данных, а также для принятия обоснованных решений на основе этих данных.
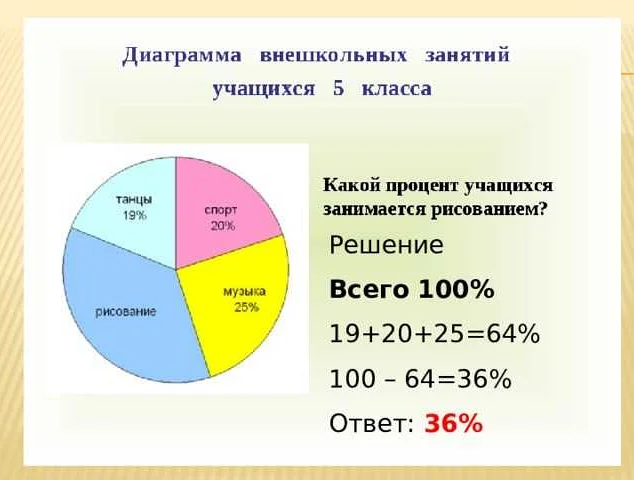
Круговая диаграмма
Круговая диаграмма используется для наглядного отображения сравнительных долей или процентного соотношения различных категорий или элементов внутри целого.
Для построения круговой диаграммы необходимо знать абсолютные значения или процентное соотношение каждой категории. Эти значения представляются в виде угловых секторов, которые занимают определенную часть круга.
Круговая диаграмма может быть полной, когда все категории представлены, или частичной, когда только некоторые категории показаны.
Для более эффективного представления данных в круговой диаграмме рекомендуется использовать различные цвета или шаблоны для каждой категории. Также можно добавить легенду, которая позволяет идентифицировать каждую категорию по цвету или шаблону.
Круговая диаграмма позволяет быстро и наглядно сравнить доли или процентное соотношение различных категорий. Она широко используется в статистике, экономике, маркетинге, социологии и других областях, где необходимо визуально представить данные и сделать выводы на основе их сравнения.
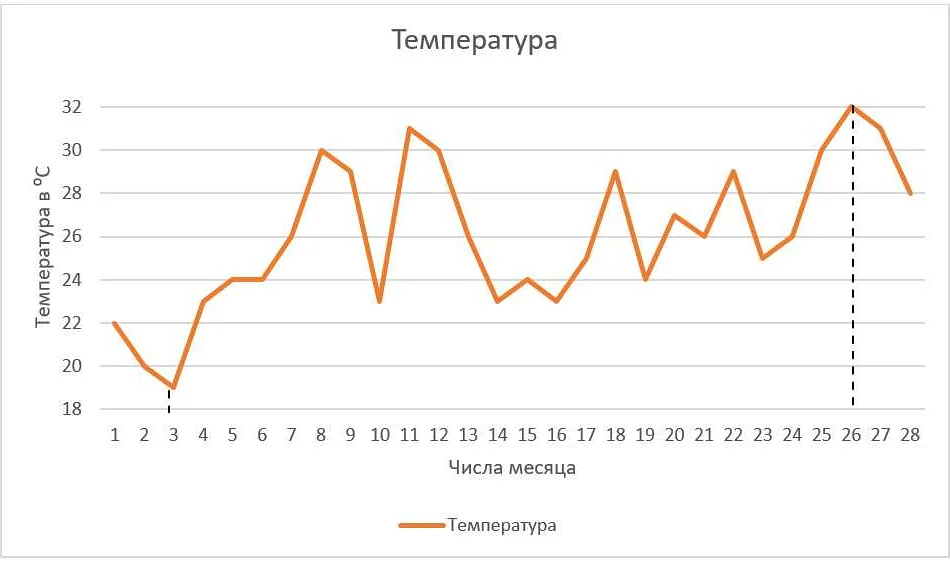
Линейная диаграмма
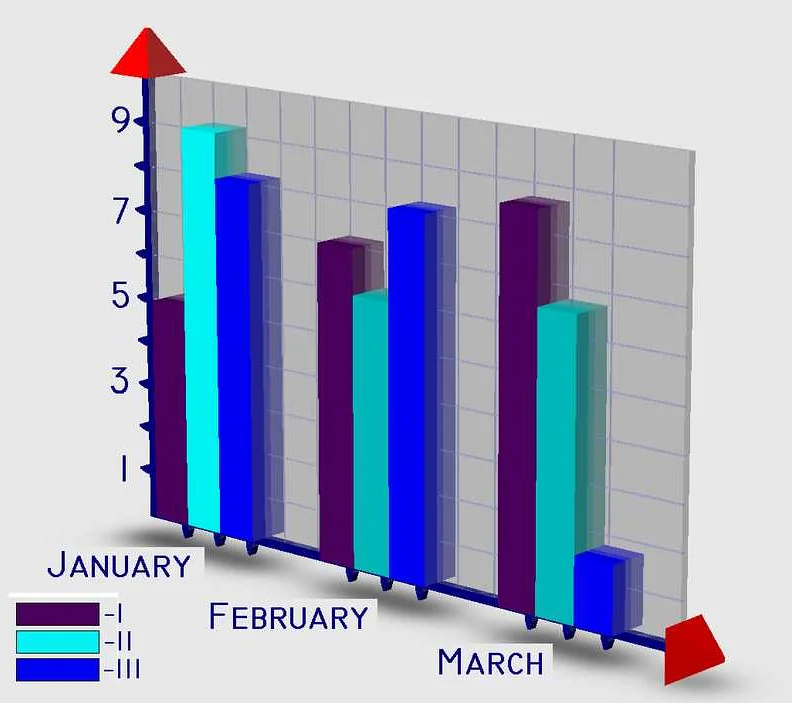
Основной элемент линейной диаграммы — линия, которая соединяет точки, значения которых соответствуют значениям двух переменных. По горизонтальной оси откладываются значения независимой переменной, а по вертикальной оси — значения зависимой переменной.
Важным аспектом линейной диаграммы является ее наглядность. Она позволяет легко определить тренды, периодические колебания или другие закономерности в данных. Также линейная диаграмма позволяет сравнивать значения разных переменных в разных точках.
Для создания линейной диаграммы часто используются различные программы, такие как Microsoft Excel или Google Таблицы. Эти программы предоставляют возможность выбрать тип диаграммы, задать значения переменных и настроить ее внешний вид.
Важно отметить, что линейная диаграмма может быть как простой, состоящей из нескольких точек, так и сложной, содержащей множество точек и дополнительную информацию, такую как легенда, маркеры или границы.
Таким образом, линейная диаграмма является мощным инструментом для представления данных в математике, позволяющим увидеть зависимости и тренды между переменными и облегчить их анализ.
Гистограмма

В гистограмме ось X представляет различные категории или значения, а ось Y показывает количество или частоту появления каждого значения. Высота столбцов гистограммы пропорциональна значениям, которые они представляют. Гистограммы могут быть составлены как для дискретных, так и для непрерывных данных.
Для создания гистограммы данные разбиваются на равные интервалы, называемые классами или группами. Затем вычисляется частота появления значений в каждом интервале и строятся прямоугольные столбцы на графике. Ширина столбцов определяется размером интервала, а высота — частотой появления значений.
КатегорияЧастота
| Категория 1 | 10 |
| Категория 2 | 15 |
| Категория 3 | 8 |
| Категория 4 | 12 |
В данной гистограмме показано распределение данных по четырем категориям. Столбцы гистограммы имеют разные высоты, что отражает различную частоту появления значений в каждой категории.
Вопрос-ответ:
Что такое диаграмма в математике?
Диаграмма в математике — это графическое представление данных или математических концепций. Она помогает наглядно показать взаимосвязи и зависимости между различными элементами.
Какие основные понятия связаны с диаграммой в математике?
Основные понятия, связанные с диаграммой в математике, включают масштаб, оси, столбцы, точки, линии, графики функций и диаграммы рассеяния.
Какие способы представления данных с помощью диаграмм существуют?
Существует несколько способов представления данных с помощью диаграмм, таких как столбчатая диаграмма, линейная диаграмма, круговая диаграмма, диаграмма рассеяния и гистограмма.
Какие преимущества использования диаграмм в математике?
Использование диаграмм в математике позволяет наглядно представить данные, облегчает анализ и сравнение информации, помогает выявить закономерности и тенденции.
Какие недостатки могут быть у диаграмм в математике?
Некоторые недостатки диаграмм в математике включают возможность искажения данных, сложность интерпретации для неподготовленного читателя и ограниченность в представлении сложных математических концепций.
Какие основные понятия связаны с диаграммами в математике?
Основные понятия, связанные с диаграммами в математике, включают такие термины, как оси координат, отрезки, точки, отметки на осях, интервалы, площадь, объем и др.
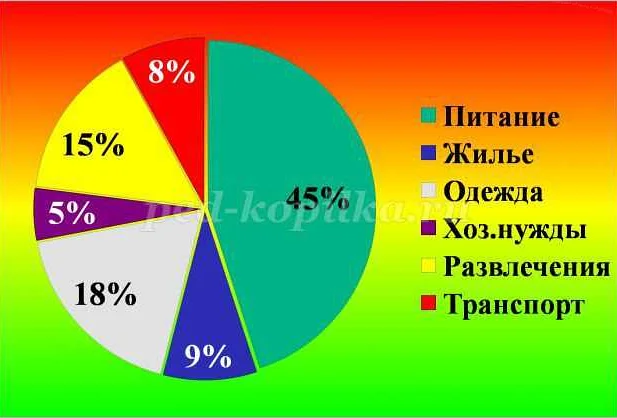
В математике диаграмма является важным инструментом для визуализации и анализа данных. Она помогает наглядно представить информацию, что позволяет лучше понять закономерности и связи между различными явлениями. Диаграммы могут быть разных типов, в зависимости от того, какую информацию они представляют. Например, столбчатые диаграммы отображают количество или значения различных категорий на оси X, в то время как круговые диаграммы демонстрируют соотношение частей к целому. Диаграмма рассеяния показывает зависимость между двумя переменными, а линейная диаграмма отображает изменение значения величины во времени. Для создания диаграмм в математике используются различные инструменты, такие как графические редакторы или специальные программы. Важно уметь выбрать подходящий тип диаграммы для представления данных, чтобы она была понятной и информативной. Диаграммы могут быть полезны не только в математике, но и в других областях знания, таких как экономика, психология, медицина и т.д. Они помогают увидеть тренды, сравнить данные и сделать выводы на основе полученной информации. В общем, использование диаграмм в математике является важным элементом анализа данных и позволяет наглядно представить информацию, что делает ее более понятной и доступной для всех.
Статья очень понятно и доступно объясняет, что такое диаграмма в математике. Я всегда слышала о диаграммах, но никогда не понимала, как они работают и зачем нужны. Теперь все стало ясно! Диаграмма — это наглядное представление данных, которое помогает лучше понять их структуру и взаимосвязи. Очень интересно узнать, что существует разные типы диаграмм, такие как столбчатая, круговая, линейная и т.д., каждая из которых подходит для определенного типа данных. Например, столбчатая диаграмма удобна для сравнения величин, а круговая показывает соотношение разных частей в целом. Теперь я понимаю, что диаграммы — это не просто красивые картинки, а мощный инструмент для анализа данных. Я уверена, что эта информация пригодится мне не только в математике, но и в других областях жизни, где важно наглядно представить информацию.