Что означает дисперсия в математике

Дисперсия в математике — это мера разброса данных вокруг среднего значения. Чем больше дисперсия, тем больше разброс данных. В этой статье вы узнаете, как вычислить дисперсию и как она используется для анализа данных.

Дисперсия – это один из основных показателей, используемых в математической статистике для измерения разброса значений в выборке или случайной величины. Она позволяет оценить, насколько значения отклоняются от среднего значения и характеризует степень разброса данных.

Для расчета дисперсии необходимо знать значения каждого элемента выборки и среднее значение. Она вычисляется как среднее арифметическое квадратов отклонений значений от среднего значения. Такой подход позволяет учесть все значения их исходной величины.

Например, чтобы рассчитать дисперсию оценок студентов по математике, необходимо знать каждую оценку и среднюю оценку по данному предмету. Затем нужно вычислить разность между каждой оценкой и средней оценкой, возвести каждую разность в квадрат, сложить все квадраты и разделить полученную сумму на количество оценок.

Дисперсия широко применяется в научных исследованиях, финансовой аналитике, экономике и других областях, где необходимо оценить разброс данных и сделать выводы о их степени вариабельности.

Определение дисперсии

Математически, дисперсия определяется как среднее значение квадрата отклонений случайной величины от ее математического ожидания.

Формула для расчета дисперсии:

D(X) = E[(X — E(X))^2]

где D(X) – дисперсия случайной величины X, E(X) – математическое ожидание случайной величины X.

Дисперсия может принимать только неотрицательные значения. Если дисперсия равна нулю, это означает, что все значения случайной величины совпадают с ее математическим ожиданием и не имеют разброса.

Пример:

Пусть есть случайная величина X, которая может принимать значения 1, 2 и 3 с вероятностями 0.3, 0.4 и 0.3 соответственно. Математическое ожидание этой случайной величины равно:

E(X) = 1 * 0.3 + 2 * 0.4 + 3 * 0.3 = 2

Теперь рассчитаем дисперсию:

D(X) = (1 — 2)^2 * 0.3 + (2 — 2)^2 * 0.4 + (3 — 2)^2 * 0.3 = 0.2

Таким образом, дисперсия случайной величины X равна 0.2.

Формула дисперсии

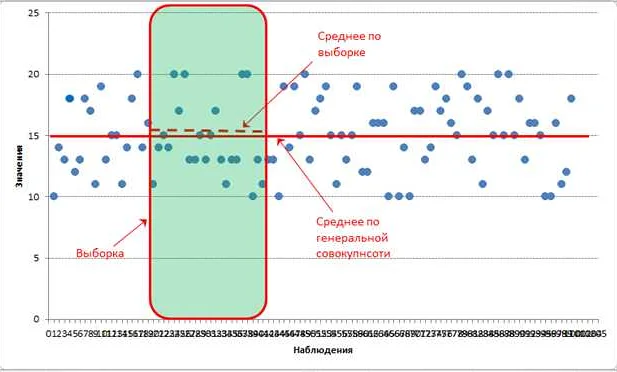
Для дискретной случайной величины:	$$D(X) = \sum_{i=1}^{n} (x_i — \bar{x})^2 \cdot P(X = x_i)$$
Для непрерывной случайной величины:	$$D(X) = \int_{-\infty}^{\infty} (x — \bar{x})^2 \cdot f(x) \, dx$$

Где:

• $$D(X)$$ — дисперсия случайной величины $$X$$;
• $$x_i$$ — значения случайной величины $$X$$;
• $$\bar{x}$$ — среднее значение случайной величины $$X$$;
• $$P(X = x_i)$$ — вероятность того, что случайная величина $$X$$ примет значение $$x_i$$ (только для дискретной случайной величины);
• $$f(x)$$ — плотность вероятности случайной величины $$X$$ (только для непрерывной случайной величины).

При расчете дисперсии необходимо вычесть среднее значение случайной величины из каждого ее значения, возвести результат в квадрат и умножить на вероятность (для дискретной случайной величины) или на плотность вероятности (для непрерывной случайной величины). Затем полученные значения суммируются (для дискретной случайной величины) или интегрируются (для непрерывной случайной величины).

Основные понятия

Для вычисления дисперсии необходимо знать значения случайной величины и ее математического ожидания. Математическое ожидание — это среднее значение случайной величины, которое можно представить как взвешенную сумму значений случайной величины, где веса — это вероятности возникновения каждого значения.

Формула для вычисления дисперсии:

1. Вычисляем математическое ожидание случайной величины.
2. Для каждого значения случайной величины вычисляем квадрат разности между значением и математическим ожиданием.
3. Для каждого значения случайной величины умножаем полученный квадрат на вероятность возникновения этого значения.
4. Суммируем все полученные произведения. Результат — это значение дисперсии.

Дисперсия может принимать только неотрицательные значения. Чем выше значение дисперсии, тем больше разброс значений случайной величины относительно ее среднего значения. Низкая дисперсия указывает на более сконцентрированные вокруг среднего значения значения случайной величины.

Среднее значение

Среднее значение можно вычислить по формуле:

Среднее значение = (сумма всех значений) / (количество элементов)

Например, если у нас есть выборка чисел 4, 6, 8, 10, то среднее значение будет:

(4 + 6 + 8 + 10) / 4 = 28 / 4 = 7

Таким образом, среднее значение этой выборки равно 7.

Среднее значение является мерой центральной тенденции и позволяет получить представление о типичном значении в выборке. Оно часто используется для описания данных и сравнения различных выборок между собой.

Отклонение

Отклонение вычисляется путем нахождения разности между каждым значением и средним значением выборки, а затем нахождения среднего арифметического от полученных разностей. Чем больше отклонение, тем больший разброс значений относительно среднего значения.

Отклонение может быть положительным или отрицательным в зависимости от того, насколько значение больше или меньше среднего значения. Модуль отклонения используется для учета только величины различия, игнорируя его направление.

Пример:

Пусть у нас есть выборка значений: 4, 6, 8, 10. Сначала найдем среднее значение: (4 + 6 + 8 + 10) / 4 = 28 / 4 = 7. Затем найдем отклонение каждого значения от среднего значения: 4 — 7 = -3, 6 — 7 = -1, 8 — 7 = 1, 10 — 7 = 3. Найдем среднее арифметическое от полученных разностей: (-3 — 1 + 1 + 3) / 4 = 0. Отклонение выборки равно 0, что означает, что значения находятся ровно вокруг среднего значения.

Примеры использования

Дисперсия широко используется в статистике для анализа разброса данных. Рассмотрим несколько примеров ее применения:

1. Финансовые рынки

В финансовой аналитике дисперсия может использоваться для измерения волатильности цен на акции, валюты или другие финансовые инструменты. Чем выше значение дисперсии, тем больше разброс цен, что указывает на более высокий уровень риска.

2. Качество производства

В производственной сфере дисперсия может быть полезна для оценки степени отклонения результатов производства от заданных стандартов. Чем больше дисперсия, тем больше разброс значений и, следовательно, больше вероятность некачественной продукции.

3. Медицинская статистика

Дисперсия может применяться в медицинской статистике для анализа разброса результатов испытаний или измерений. Например, дисперсия может использоваться для определения степени вариабельности показателей здоровья пациентов или эффективности лекарственных препаратов.

Все эти примеры демонстрируют, что дисперсия является полезным инструментом для измерения и анализа разброса данных, что позволяет принимать более обоснованные решения в различных областях деятельности.

Пример 1: Распределение оценок

Рассмотрим пример с распределением оценок по математике в классе. Предположим, что в классе из 20 учеников было проведено контрольное задание, за которое ученики могли получить от 0 до 10 баллов.

Результаты контрольной работы представлены в таблице:

УченикОценка

Алексей	7
Иван	8
Мария	5
Анна	9
Дмитрий	6
Елена	7
Михаил	4
Ольга	8
Павел	7
Светлана	6
Татьяна	9
Артем	6
Виктория	5
Георгий	8
Екатерина	7
Ирина	9
Константин	4
Лариса	6
Николай	3
Олег	9

Для вычисления дисперсии в данном примере необходимо рассчитать среднее значение оценок и отклонение каждой оценки от среднего значения. Далее, эти отклонения нужно возвести в квадрат, сложить их и разделить на количество оценок.

После проведения расчетов получаем, что средняя оценка равна 6.85, а дисперсия равна 2.47.

Вопрос-ответ:

Что такое дисперсия?

Дисперсия — это мера разброса значений случайной величины относительно ее среднего значения. Она показывает, насколько далеко от среднего значения могут быть наблюдаемые значения случайной величины.

Как вычислить дисперсию?

Для вычисления дисперсии нужно вычислить среднее значение случайной величины и отнять это значение от каждого наблюдаемого значения, затем возвести полученное число в квадрат, сложить все полученные значения и поделить на количество наблюдений.

Зачем нужна дисперсия?

Дисперсия нужна для измерения степени разброса значений случайной величины. Она позволяет оценить, насколько предсказуемы или разнообразны значения данной величины, что помогает в анализе данных и принятии решений.

Как дисперсия связана с стандартным отклонением?

Стандартное отклонение — это квадратный корень из дисперсии. Оно также является мерой разброса значений случайной величины, но выражается в тех же единицах, что и сама случайная величина, в отличие от дисперсии.

Можно ли использовать дисперсию для сравнения различных наборов данных?

Да, дисперсия может быть использована для сравнения различных наборов данных. Чем больше дисперсия, тем больше разброс значений в данных. Поэтому, если два набора данных имеют схожие средние значения, но различные дисперсии, можно сказать, что данные с большей дисперсией имеют более разнообразные значения.

Пример 2: Измерение погрешности

Представим, у нас есть экспериментальные данные о температуре воздуха за каждый день недели. Мы измерили температуру воздуха в градусах Цельсия и получили следующие значения:

Понедельник: 20°C

Вторник: 21°C

Среда: 19°C

Четверг: 20.5°C

Пятница: 19.5°C

Мы хотим определить, насколько сильно разнятся наши измерения. Для этого мы можем вычислить дисперсию значений температуры.

Сначала нам нужно найти среднее значение температуры. Для этого мы суммируем все измерения и делим на их количество:

Среднее значение = (20 + 21 + 19 + 20.5 + 19.5) / 5 = 20°C

Теперь мы можем вычислить отклонение каждого значения от среднего:

Отклонения: -0.5°C, 1°C, -1°C, 0.5°C, -0.5°C

Затем мы возводим каждое отклонение в квадрат, чтобы избавиться от отрицательных значений:

Квадраты отклонений: 0.25°C, 1°C, 1°C, 0.25°C, 0.25°C

Наконец, мы суммируем все квадраты отклонений и делим на количество измерений минус одно, чтобы получить дисперсию:

Дисперсия = (0.25 + 1 + 1 + 0.25 + 0.25) / (5 — 1) = 0.875°C²

Таким образом, в данном примере дисперсия значений температуры составляет 0.875°C². Это позволяет нам оценить степень разброса измерений и измерить погрешность наших данных.

Видео по теме: