Как обозначается среднее в математике: формула и примеры

Среднее значение в математике обозначается как средний арифметический, т.е. сумма всех значений, поделенная на их количество. Он широко используется в статистике и анализе данных. Узнайте, как правильно вычислять среднее значение и применять его в решении задач.

Среднее значение, как правило, является одним из первых понятий, введенных в математический анализ. Оно используется для определения центральной тенденции множества чисел. Среднее значение может принимать различные формы, такие, как среднее арифметическое, медиана, мода и гармоническое среднее, каждый из которых имеет свою сферу применения.

Среднее арифметическое является, пожалуй, самой распространенной формой среднего значения и используется для определения среднего значения набора чисел, путем деления суммы всех чисел на количество чисел в наборе. Медиана, с другой стороны, является центральным значением в упорядоченном наборе чисел и находится в середине набора чисел.

Мода — это значение, которое появляется наиболее часто в наборе чисел. Гармоническое среднее используется для нахождения среднего значения двух величин, таких как скорость и расстояние, используемых в физике.

В этой статье мы более подробно рассмотрим каждый вид среднего значения и дадим практические примеры, чтобы помочь вам лучше понять, как они работают и как их использовать в различных ситуациях.

Определение термина «среднее»

Среднее — это математическая характеристика набора чисел, которая показывает общую тенденцию этого набора чисел. Рассчитывается на основе арифметических операций, таких как сложение, деление и вычитание.

Существует три основных вида среднего: среднее арифметическое, среднее геометрическое и среднее гармоническое.

Среднее арифметическое — это сумма всех чисел в наборе, деленная на количество чисел в наборе. Среднее геометрическое — это корень из произведения всех чисел в наборе. Среднее гармоническое — это обратное значение среднего арифметического инвертированное на каждое число в наборе, а затем снова инвертированное на количество чисел в наборе.

Средние значения часто используются в математике, статистике, науке, экономике и других областях, чтобы описать и проанализировать данные. Они удобны для подсчета и сравнения наборов чисел, таких как зарплаты, продолжительность жизни, налоги и т.д.

• Среднее арифметическое самое распространенное среднее значение;
• Среднее геометрическое наиболее часто используется в случае, когда нужно усреднить относительные изменения, например, в геометрических прогрессиях;
• Среднее гармоническое наиболее подходит для усреднения процентных соотношений или скоростей.

Что бы ни использовалось, правильное понимание средних значений может помочь нам лучше понимать данные и принимать более обоснованные решения.

Разновидности средних значений

Среднее арифметическое (среднее значение) — это наиболее распространенный тип среднего значения. Оно вычисляется как сумма всех значений, деленная на количество значений в выборке. Среднее значение может использоваться для описания центральной тенденции в выборке.

Медиана — это значение, которое делит ряд значений пополам. Если количество значений в выборке четное, медианой считается среднее арифметическое двух средних значений. Медиана является показателем, который не подвержен всяким выбросам в данных и может использоваться для описания центра распределения.

Мода — это значение, которое появляется наиболее часто в выборке. Мода может быть использована для описания формы распределения.

Гармоническое среднее — это среднее гармоническое значение всех значений в выборке. Гармоническое среднее может использоваться для расчета среднего значения величин с разными долями в общей выборке.

Среднее квадратичное отклонение — это мера распределения значений относительно их среднего значения. Она используется для расчета стандартного отклонения и может быть полезной для определения уровня изменчивости данных в выборке.

Геометрическое среднее — это среднее геометрическое значение всех значений в выборке. Геометрическое среднее может использоваться для расчета среднего значения величин с разными долями в общей выборке.

Взвешенное среднее — это среднее значение, которое учитывает вклад каждого значения в выборке, умноженного на его вес. Взвешенное среднее может использоваться для описания средней цены на акции в компании с различным количеством выпущенных акций.

• Среднее арифметическое — наиболее распространенный тип среднего значения.
• Медиана — значение, которое делит ряд значений пополам.
• Мода — значение, которое появляется наиболее часто.
• Гармоническое среднее — среднее гармоническое значение всех значений.

1. Среднее арифметическое — наиболее распространенный тип среднего значения.
2. Медиана — значение, которое делит ряд значений пополам.
3. Мода — значение, которое появляется наиболее часто.
4. Гармоническое среднее — среднее гармоническое значение всех значений.

Тип среднего значенияОписание

Среднее арифметическое	Наиболее распространенный тип среднего значения.
Медиана	Значение, которое делит ряд значений пополам.
Мода	Значение, которое появляется наиболее часто.
Гармоническое среднее	Среднее гармоническое значение всех значений.

Среднее арифметическое: формула и примеры расчета

Среднее арифметическое — это мера центральной тенденции, которая вычисляется путем добавления всех значений и деления на количество этих значений. Формула для вычисления среднего арифметического имеет вид:

(x1 + x2 + … + xn) / n

где x1, x2, …, xn — значения, n — количество значений.

Например, для расчета среднего арифметического величин 5, 7 и 9, мы должны выполнить следующие действия:

(5 + 7 + 9) / 3 = 7

Значит, среднее арифметическое для этих трех чисел равно 7.

Среднее арифметическое может быть использовано для вычисления различных статистических параметров, таких как медиана или мода. Оно также является важным концептом в экономике, финансах и других областях.

Медиана: определение и методы расчета

Медиана – это центральный элемент в упорядоченном ряду данных, который разделяет ряд на две равные части. То есть, половина значений находится выше медианы, а другая половина – ниже. Например, медиана списка 1, 2, 3, 4, 5 равна 3, потому что она делит этот список на две равные части: 1, 2 и 4, 5.

Чтобы найти медиану, необходимо:

1. Упорядочить данные по возрастанию или убыванию.
2. Определить, содержит ли ряд нечетное количество элементов. Если да, то медианой будет элемент, который находится по середине списка. Если же количество элементов четное, то медианой будет среднее значение двух центральных элементов списка.

Например, чтобы найти медиану списка 1, 5, 3, 2, 4, необходимо упорядочить его по возрастанию: 1, 2, 3, 4, 5. Поскольку в этом списке четное количество элементов, медианой будет среднее значение двух центральных элементов, то есть (3+4)/2 = 3.5.

ДанныеУпорядоченные данныеМедиана

1, 5, 3, 2, 4	1, 2, 3, 4, 5	3.5
2, 4, 6, 8, 10, 12	2, 4, 6, 8, 10, 12	7
3, 8, 12, 15	3, 8, 12, 15	10

Медиана широко используется в статистике, экономике, биологии и других областях, где требуется описать центральную тенденцию набора данных. Она является альтернативой среднему значению и более устойчива к выбросам.

Квартили и перцентили: что это такое и как их находить

Квартили и перцентили — это показатели, которые используются в статистике для описания распределения данных. Они позволяют нам понять, как данные распределены вокруг среднего значения.

Квартили делят данные на четыре равные части: первый квартиль (Q1) указывает на значение, ниже которого находятся 25% данных, второй квартиль (Q2) соответствует медиане, и третий (Q3) — значение, ниже которого находятся 75% данных.

Перцентили позволяют нам разбить данные на 100 равных частей. Например, 25-й перцентиль означает значение, ниже которого находятся 25% данных, а 90-й перцентиль — значение, ниже которого находятся 90% данных.

Как находить квартили и перцентили? Для этого нужно упорядочить данные по возрастанию и найти нужные значения. Например, если нужно найти первый квартиль, нужно найти значение, которое находится на 25% от общего числа значений в наборе. Для нахождения перцентиля нужно выполнить аналогичную операцию: найти значение, которое находится на нужном проценте от общего числа значений.

Квартили и перцентили важны при работе с данными, так как они помогают понять, как данные распределяются вокруг среднего значения.

Среднее геометрическое и среднее гармоническое: особенности расчета

Среднее геометрическое — это среднее значение, получаемое путем умножения всех чисел и извлечения из их произведения корня степени, равной количеству чисел. Например, чтобы найти среднее геометрическое чисел 2, 3 и 5, нужно умножить их (2 x 3 x 5 = 30) и извлечь кубический корень из 30 (около 3.11).

Среднее гармоническое — это среднее значение, равное инвертированной сумме инвертированных чисел, деленной на количество чисел. Например, чтобы найти среднее гармоническое чисел 2, 3 и 5, нужно инвертировать их (1/2, 1/3 и 1/5), сложить их (1/2 + 1/3 + 1/5 = 31/30) и инвертировать результат (30/31, около 0.967).

Среднее геометрическое и среднее гармоническое имеют различные применения в математике. Среднее геометрическое подходит для нахождения среднего значения величин, умножение которых дает некоторый результат (например, скорость, расстояние и время). Среднее гармоническое же используется в задачах, связанных с пропорциями и средним временем, скоростью и т.д.

Несмотря на то, что среднее геометрическое и среднее гармоническое могут быть сложными в расчетах, они являются важными инструментами в математических исследованиях и практических применениях.

Взвешенное среднее: определение и примеры расчета

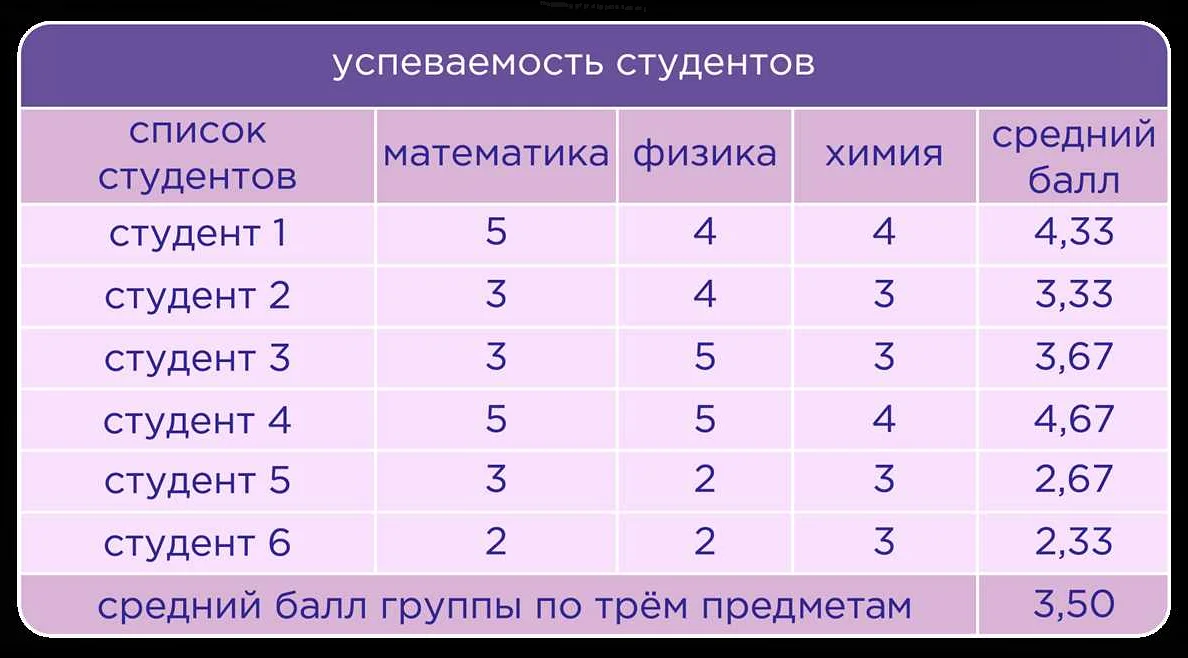
Взвешенное среднее — это среднее значение, в котором каждая величина имеет свой вес, то есть свой вклад в результирующее значение. Оценки с большим весом имеют большее значение в расчете взвешенного среднего, чем оценки с меньшим весом.

Формула для расчета взвешенного среднего:

Взвешенное среднее = (x1 * w1 + x2 * w2 + … + xn * wn) / (w1 + w2 + … + wn)

Где:

x1, x2, …, xn — значения, которые нужно усреднить

w1, w2, …, wn — вес каждого значения

Пример 1: Расчет средней оценки студентов по предмету, где некоторые оценки имеют больший вес. Если у 10 студентов оценки 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, тогда мы можем присвоить веса

• 4 имеет вес 2
• 5 имеет вес 8

Тогда:

Взвешенное среднее = (4 * 2 + 5 * 8) / (2 + 8) = 4.8

Пример 2: Расчет средней цены продажи автомобиля с учетом года выпуска и пробега. Если у нас есть 3 автомобиля:

АвтомобильГод выпускаПробегЦена

Автомобиль 1	2005	150000	200000
Автомобиль 2	2010	80000	350000
Автомобиль 3	2015	5000	600000

Тогда мы можем присвоить веса:

Автомобиль 1 — вес 2

Автомобиль 2 — вес 3

Автомобиль 3 — вес 5

Тогда:

Взвешенное среднее = (200000 * 2 + 350000 * 3 + 600000 * 5) / (2 + 3 + 5) = 436666.67

Выборочное и полное среднее: какие бывают отличия

Выборочное и полное среднее — это две распространенные формы расчета среднего значения, используемого в математике и статистике. Полное среднее вычисляется путем деления суммы всех значений набора на количество этих значений, тогда как выборочное среднее вычисляется только на основе выборки из набора значений.

Отличия между выборочным и полным средним заключаются в том, что выборочное среднее дает оценку среднего значения для выбранной группы, в то время как полное среднее предоставляет среднее значение всего множества значений. Следовательно, выборочное среднее может быть менее точным представлением среднего значения, особенно если выборка не отображает всего набора данных.

Выборочное среднее обычно используется при обработке больших объемов данных, когда полное среднее требует слишком много времени и ресурсов. Однако, если точность критически важна, особенно при работе с относительно небольшими выборками, полное среднее может быть предпочтительным методом.

Использование правильного метода расчета среднего значения зависит от целей анализа и объема данных, доступных для анализа. Поэтому, при выборе метода расчета следует оценить точность, вычислительные ресурсы и объем данных, которые могут быть использованы в анализе.

Дисперсия и стандартное отклонение: от чего зависят и как находить

Дисперсия и стандартное отклонение — это показатели, используемые в математической статистике для измерения разброса значений в выборке. Дисперсия выражает среднеквадратическое отклонение от математического ожидания, а стандартное отклонение — среднеквадратическое отклонение от среднего значения.

Дисперсия зависит от среднеквадратического отклонения, которое в свою очередь зависит от разброса значений в выборке. Чем больше разброс, тем выше дисперсия. Также дисперсия может быть высокой, если есть выбросы в выборке или если данные не являются нормально распределенными.

Стандартное отклонение также зависит от разброса значений в выборке. Оно вычисляется как квадратный корень из дисперсии и измеряется в тех же единицах, что и изначальные данные. Чем выше стандартное отклонение, тем больше вариации в данных и тем менее репрезентативная выборка.

• Чтобы найти дисперсию, нужно вычислить среднее значение квадратов отклонений каждого значения в выборке от среднего значения.
• Чтобы найти стандартное отклонение, нужно вычислить квадратный корень из дисперсии.

Дисперсия и стандартное отклонение могут использоваться для оценки качества данных и для обнаружения выбросов в выборке. Они также используются в различных областях, например, в физике, экономике и медицине.

Смещенное и несмещенное отклонение: различия и применение

Отклонение — это мера разброса данных вокруг среднего значения. Она позволяет оценить, насколько значения в наборе данных отличаются друг от друга.

Смещенное отклонение — это наиболее распространенный способ измерения отклонения. Для его вычисления берется среднее арифметическое отклонений каждого значения от среднего значения.

Формула смещенного отклонения:

σ = √(Σ(xi — x̅)² / n)

где:

• σ — смещенное отклонение
• Σ — сумма всех значений
• xi — отдельные значения в наборе данных
• x̅ — среднее значение
• n — общее количество значений

Несмещенное отклонение — это более точный способ измерения отклонения, который используется в случаях, когда рассматривается небольшой набор данных. Для его вычисления необходимо делить сумму квадратов отклонений каждого значения от среднего значения на n-1 вместо n.

Формула несмещенного отклонения:

s= √(Σ(xi — x̅)² / (n-1))

где:

• s — несмещенное отклонение
• Σ — сумма всех значений
• xi — отдельные значения в наборе данных
• x̅ — среднее значение
• n — общее количество значений в наборе данных

Отличие между смещенным и несмещенным отклонением заключается в том, что смещенное отклонение недооценивает изменчивость данных в небольшом наборе данных. Несмещенное отклонение же обеспечивает более точную оценку изменчивости данных, когда общее количество значений меньше 30.

Правильно выбранное отклонение помогает более точно выразить зависимости и сделать предсказания.

Среднее в математике и статистике: важность и применение в реальной жизни

Среднее, или среднее значение, является одним из основных понятий в математике и статистике. Среднее значение вычисляется путем сложения значений их последующего деления на количество значений. В практическом применении среднее значение используется для определения центральной тенденции данных.

В реальной жизни среднее значение имеет множество применений. Например, в экономике оно используется для определения среднего дохода или стоимости товаров и услуг. В физике среднее значение используется для определения среднего значения скорости или силы. В медицине, среднее значение может быть использовано для вычисления средней дозы лекарства или определения среднего времени выздоровления.

В добавление, среднее значение может использоваться для анализа больших объемов данных и выявления тенденций и закономерностей. Например, среднее значение расходов на питание или расходов на транспорт за год позволяет сделать выводы о стабильности или изменении уровня жизни населения.

Вопрос-ответ:

Что такое среднее значение в математике?

Среднее значение – это сумма всех значений, деленная на их количество. Оно используется в математике как показатель центральной тенденции выборки (совокупности данных). Среднее значение может быть средним арифметическим, средним геометрическим, средним гармоническим и т.д.

Как вычислить среднее значение?

Для вычисления среднего значения нужно сложить все значения и разделить сумму на их количество. То есть, если у вас есть 5 чисел: 2, 4, 5, 7, 9, то чтобы вычислить их среднее значение, нужно сложить эти числа (2+4+5+7+9=27) и разделить на их количество (27/5=5,4).

Какая разница между средним арифметическим, средним гармоническим и средним геометрическим?

Среднее арифметическое – это сумма всех значений, деленная на их количество. Среднее гармоническое – это обратное значение среднего арифметического от обратных значений. Среднее геометрическое – это корень n-ой степени произведения всех значений. Выбор между этими тремя типами среднего значения зависит от того, как вы собираетесь использовать данные.

Как использовать среднее значение в статистике?

Среднее значение используется в статистике как показатель центральной тенденции выборки (среднее арифметическое) и как гармоническое среднее в некоторых случаях, например, когда требуется усреднить скорость или температуру. Оно используется для обобщения большого объема данных и упрощения их интерпретации.

Может ли среднее значение быть неправильным?

Да, среднее значение может быть неправильным, если выборка содержит выбросы или ошибки. Иногда неправильное среднее значение может быть результатом неверного использования различных методов вычисления. Поэтому важно выбирать правильный метод среднего значения и внимательно проверять данные на наличие ошибок.

Можно ли использовать среднее значение для интерпретации относительных изменений?

Нет, нельзя использовать среднее значение для интерпретации относительных изменений, потому что оно может быть искажено выбросами. Для этой цели лучше использовать процентное изменение или изменение в процентах от среднего значения.

Как выбрать правильный метод среднего значения?

Выбор метода среднего значения зависит от типа данных и цели исследования. Например, если у вас есть данные с разными единицами измерения, то среднее гармоническое может быть лучшим выбором. Если данные содержат выбросы, то среднее арифметическое не является надежным показателем и лучше использовать медиану. В общем, нужно выбирать метод в зависимости от конкретной ситуации.

Видео по теме: