Что такое гипер в математике

Гипер в математике — это префикс, указывающий на превышение или сверх- в отношении какого-либо понятия или явления. В данной статье рассматривается значение гипер в различных математических контекстах и его применение в алгебре, геометрии и теории чисел. Узнайте, как гипер помогает нам понять и описать сложные и расширенные концепции в мире математики.

Гипер — это математический термин, который часто используется в геометрии и алгебре. Гипер — это префикс, который обозначает связь с объектами, имеющими больше чем три измерения или свойствами, выходящими за рамки обычных представлений.

В геометрии гипер может относиться к гиперповерхности, которая является обобщением понятия поверхности на пространства большей размерности. Например, гиперповерхность может быть плоскостью в трехмерном пространстве или сферой в четырехмерном пространстве.

В алгебре гипер может относиться к гиперкомплексным числам, которые являются обобщением комплексных чисел на пространства большей размерности. Гиперкомплексные числа могут иметь более чем два компонента и обладать различными свойствами, которые не характерны для обычных действительных или комплексных чисел.

Например, кватернионы — это гиперкомплексные числа, которые имеют четыре компонента и используются в роторной алгебре и компьютерной графике для представления и вращения объектов в трехмерном пространстве.

Таким образом, гипер в математике относится к объектам и свойствам, которые выходят за рамки обычных представлений и имеют большую размерность или сложность. Гипер является важным понятием в различных областях математики и находит применение в различных науках и технологиях.

Понятие гипер в математике

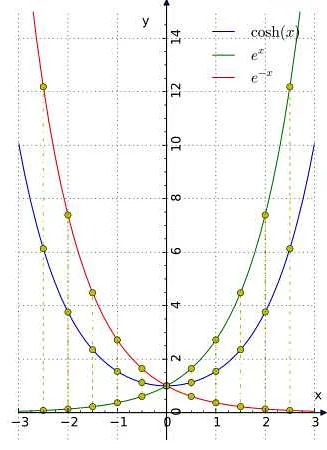
Одним из наиболее известных примеров гипер в математике является гиперплоскость. Гиперплоскость — это обобщение понятия плоскости на пространства высокой размерности. Гиперплоскость в трехмерном пространстве представляет собой плоскость, которая разделяет пространство на две части. Аналогично, гиперплоскость в n-мерном пространстве разделяет пространство на две n-1-мерные части.

Гиперкуб — это другой пример гипер в математике. Гиперкуб — это обобщение понятия куба на пространства высокой размерности. Гиперкуб в двумерном пространстве представляет собой квадрат, в трехмерном — куб, а в n-мерном пространстве — n-мерный куб. Гиперкуб обладает свойствами, характерными для куба, но в более высоких размерностях.

Таким образом, понятие гипер в математике используется для обозначения объектов, которые выходят за рамки обычных геометрических размерностей или свойств. Гиперплоскости и гиперкубы — это лишь некоторые примеры гипер в математике, а существует множество других гиперобъектов, которые изучаются в различных областях математики и физики.

Какие виды гиперов существуют

В математике существует несколько видов гиперов, которые можно классифицировать по различным признакам:

1. Гиперплоскости: это гиперы, которые имеют на одну размерность меньше, чем окружающее пространство. Например, гиперплоскость в трехмерном пространстве — это плоскость.

2. Гиперкубы: это гиперы, которые являются обобщением понятия куба на большее количество измерений. Гиперкуб в двухмерном пространстве — это квадрат, в трехмерном — это обычный куб, а в более высоких измерениях это аналогичные фигуры.

3. Гиперсферы: это гиперы, которые являются обобщением понятия сферы на большее количество измерений. Гиперсфера в двухмерном пространстве — это окружность, в трехмерном — это обычная сфера, а в более высоких измерениях это аналогичные фигуры.

4. Гиперграфы: это гиперы, которые представляют собой обобщение понятия графа на большее количество измерений. В гиперграфах ребра могут связывать более двух вершин. Например, в трехмерном пространстве гиперграф может быть представлен в виде поверхности, на которой ребра связывают более двух вершин.

Это лишь несколько примеров видов гиперов, которые существуют в математике. Каждый из них имеет свои особенности и применения в различных областях науки и техники.

Определение гиперплоскости в математике

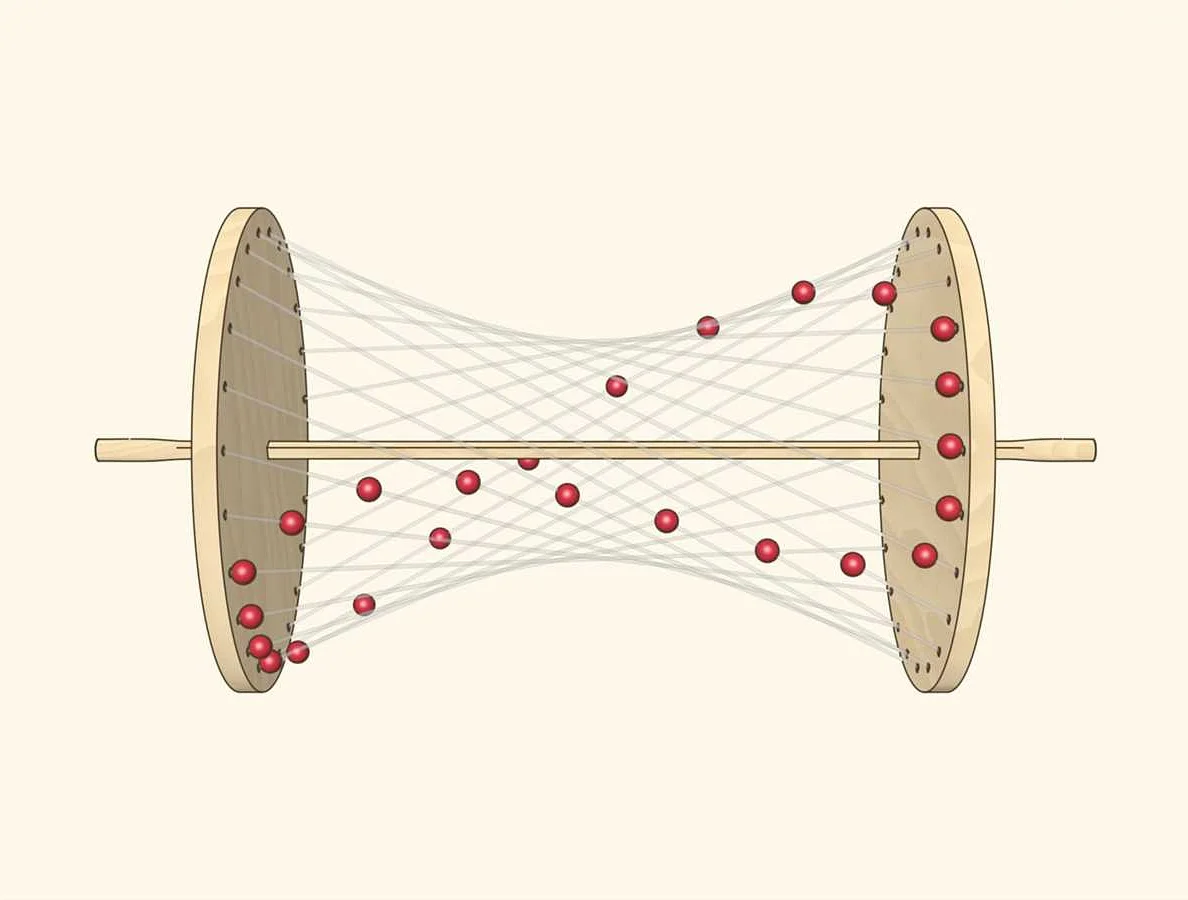
ax_1 + bx_2 + … + cx_n + d = 0,

где a, b, c, d — коэффициенты, и x_1, x_2, …, x_n — переменные.

Уравнение гиперплоскости имеет решение, если некоторые значения переменных удовлетворяют уравнению. Гиперплоскость может быть задана в виде векторного уравнения:

v · n = d,

где v — вектор, n — нормальный вектор гиперплоскости, и d — скаляр.

Гиперплоскость широко используется в линейной алгебре, геометрии, оптимизации и других областях математики. Она играет важную роль в разделении и классификации данных, построении моделей и решении задач.

Гипергеометрическое распределение: пример использования гипера

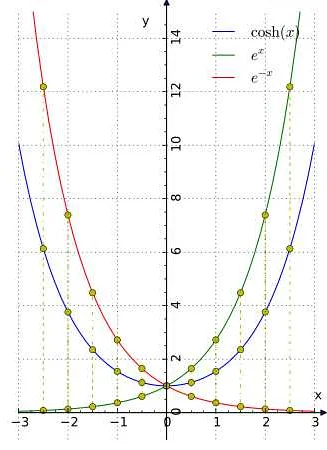
Представим ситуацию, в которой в урне содержится 10 красных шаров и 5 синих шаров. Мы хотим выбрать 3 шара из этой урны. Вероятность выбора определенного количества красных шаров будет описываться гипергеометрическим распределением.

Пример использования гипергеометрического распределения:

1. Задача: Найти вероятность выбора 2 красных шара из урны с 10 красными шарами и 5 синими шарами при выборе 3 шаров.
2. Решение: Используем формулу для гипергеометрического распределения:
   • P(X = 2) = (C(10, 2) * C(5, 1)) / C(15, 3)
   • Где C(n, k) обозначает количество сочетаний из n элементов по k.
   • P(X = 2) — вероятность выбора 2 красных шара.
   • C(10, 2) — количество сочетаний из 10 красных шаров по 2.
   • C(5, 1) — количество сочетаний из 5 синих шаров по 1.
   • C(15, 3) — количество сочетаний из 15 шаров по 3.
3. Вычисляем значение:
   • P(X = 2) = (C(10, 2) * C(5, 1)) / C(15, 3)
   • P(X = 2) = (45 * 5) / 455
   • P(X = 2) ≈ 0.4945

Таким образом, вероятность выбора 2 красных шара из урны составляет примерно 0.4945.

Как гиперы применяются в теории вероятностей

В теории вероятностей гиперы используются для моделирования и анализа случайных явлений, в которых рассматриваются случайные величины с гипергеометрическим распределением. Гипергеометрическое распределение возникает в задачах, связанных с выборками без возвращения и без учета порядка. Оно часто применяется в статистике и эконометрике, а также в биологии и медицине.

Гипергеометрическое распределение позволяет решать задачи, связанные с наличием ограниченного числа объектов в выборке и определением вероятности появления определенного числа объектов с определенными характеристиками. Например, в гипергеометрическом распределении можно описать вероятность получить определенное количество белых шаров из выборки без возвращения, если изначально в выборке было ограниченное количество белых и черных шаров.

Гиперы в теории вероятностей также используются для решения задач, связанных с оценкой параметров и построением доверительных интервалов. Они позволяют учитывать особенности выборки и моделировать реальные случайные процессы.

Таким образом, гиперы играют важную роль в теории вероятностей, позволяя моделировать и анализировать различные случайные явления на основе гипергеометрического распределения. Их применение широко распространено в различных областях, где требуется анализ и оценка вероятностей, связанных с выборками без возвращения.

Гипергеометрическая функция: определение и свойства

Гипергеометрическая функция обозначается как $_2F_1(a, b; c; z)$, где a, b, c – параметры функции, а z – аргумент. Она может быть определена для различных значений параметров и аргументов.

Основные свойства гипергеометрической функции:

• Сходимость: гипергеометрическая функция сходится при $|z| < 1$, и расходится при $|z| > 1$
• Аналитическое продолжение: гипергеометрическая функция может быть продолжена на всю комплексную плоскость, кроме особых точек
• Связь с другими функциями: гипергеометрическая функция связана с многими другими специальными функциями, такими как гамма-функция и бета-функция
• Интегральное представление: гипергеометрическая функция может быть представлена через интеграл, что позволяет вычислять ее значения

Гипергеометрическая функция широко применяется в решении различных математических задач, включая решение дифференциальных уравнений, вычисление интегралов и аппроксимацию функций. Она также имеет множество свойств и особенностей, которые делают ее полезной для анализа и моделирования различных систем и процессов.

Видео по теме:

Вопрос-ответ:

Что такое гипер в математике?

В математике термин «гипер» обозначает связанные сущности или явления, имеющие отношение к гиперпространству или гипергеометрии. Гиперпространство — это обобщение понятия пространства на большее количество измерений, а гипергеометрия — это раздел математики, изучающий геометрические свойства гиперфигур.

Какие примеры гиперфигур существуют?

Одной из известных гиперфигур является гиперкуб — обобщение понятия куба на большее количество измерений. Например, в трехмерном пространстве это будет куб, а в четырехмерном — гиперкуб. Также существуют гиперсферы, гиперцилиндры и другие гиперфигуры, имеющие больше трех измерений.

Как можно представить себе гиперпространство?

Гиперпространство нельзя представить непосредственно, так как оно имеет больше трех измерений, что выходит за пределы нашего восприятия. Однако его можно представить в виде аналогии. Например, если мы живем в трехмерном пространстве и можем двигаться вперед-назад, влево-вправо и вверх-вниз, то в гиперпространстве можно двигаться еще и в других направлениях, находящихся перпендикулярно этим трем.

Какую практическую пользу можно извлечь из изучения гиперфигур?

Изучение гиперфигур имеет практическую пользу во многих областях науки и техники. Например, в компьютерной графике используются гиперфигуры для создания трехмерных моделей и анимаций. В криптографии гиперфигуры могут быть использованы для создания сложных алгоритмов шифрования. Также гиперфигуры находят применение в физике, экономике и других дисциплинах.

Можно ли представить гиперпространство в виде физической реальности?

Гиперпространство не является физической реальностью, так как оно выходит за пределы трехмерного пространства, в котором мы живем. Однако его можно представить в виде абстрактной математической модели, которая позволяет изучать и описывать определенные явления и свойства, не доступные для наблюдения в трехмерном пространстве.

Что такое гипер в математике?

В математике термин «гипер» используется для обозначения геометрических фигур и пространств, которые имеют больше, чем три измерения. Гипер может быть приставкой к различным словам, например, гиперповерхность, гиперкуб, гипергеометрическая функция и т. д. Такие объекты изучаются в различных областях математики, включая геометрию, топологию и анализ.

Примеры гипергеометрических функций в математике

Гипергеометрической функцией называется специальная функция, которая определяется с помощью гипергеометрического ряда. Эта функция играет важную роль в различных областях математики и физики, и ее применение включает в себя решение уравнений, моделирование физических систем и анализ вероятностных распределений. Вот несколько примеров гипергеометрических функций:

1. Гипергеометрическая функция второго рода (также известная как функция Лежандра) обозначается как F(a, b; c; z) и определяется следующим образом:

F(a, b; c; z) = ∑ ((a)n (b)m / (c)k) * (z)^k / (k!)

где n, m и k — натуральные числа, (a)n, (b)m и (c)k — символы Похгаммера, и z — комплексное число.

2. Гипергеометрическая функция первого рода (знаменитая функция Гаусса) обозначается как F(a, b; c; z) и определяется следующим образом:

F(a, b; c; z) = ∑ ((a)n (b)m / (c)k) * (z)^k / (k!)

где n, m и k — натуральные числа, (a)n, (b)m и (c)k — символы Похгаммера, и z — комплексное число.

3. Гипергеометрическая функция третьего рода (также известная как функция Куммера) обозначается как F(a, b; c, d; z) и определяется следующим образом:

F(a, b; c, d; z) = ∑ ((a)n (b)m / (c)k (d)l) * (z)^k / (k! l!)

где n, m, k и l — натуральные числа, (a)n, (b)m, (c)k и (d)l — символы Похгаммера, и z — комплексное число.

Это лишь несколько примеров гипергеометрических функций, и их применение широко распространено в различных математических и физических задачах.

Гиперсфера: определение и геометрические свойства

Гиперсфера определяется как множество точек в n-мерном евклидовом пространстве, равноудаленных от одной фиксированной точки, называемой центром гиперсферы. Расстояние от центра гиперсферы до любой точки на ее поверхности называется радиусом гиперсферы.

Главным геометрическим свойством гиперсферы является то, что она является геометрическим объектом с постоянной положительной кривизной во всех точках своей поверхности. Это отличает гиперсферу от других гиперповерхностей, таких как гиперплоскости или гиперцилиндры, которые могут иметь различную кривизну.

В зависимости от размерности пространства существуют различные названия для гиперсферы. Например, в трехмерном пространстве гиперсферу называют сферой, в четырехмерном — гиперсферой, в пятимерном — гипершаром и так далее.

Гиперсферы играют важную роль в различных областях математики и физики, включая геометрическую топологию, теорию относительности и теорию вероятностей. Они также находят применение в компьютерной графике и визуализации данных в высоких размерностях.