15 сфер применения теории чисел в жизни и науке

Теория чисел – увлекательная и важная дисциплина, которая находит применение во многих областях, таких как криптография, алгоритмы шифрования, теория кодов, математическая физика, компьютерная наука и многие другие. Узнайте больше о том, где и как может быть использована теория чисел.

Теория чисел — это область математики, которая изучает свойства чисел и их взаимоотношения. На первый взгляд может показаться, что это теоретическая наука, которая не имеет практического применения. Однако, это не совсем так. Теория чисел играет важную роль в различных отраслях науки и техники, а также повседневной жизни.

Среди примеров использования теории чисел в жизни можно назвать кодирование данных в информационных системах, поиск простых чисел в криптографии, анализ паролей и проверку их на стойкость к взлому. Также теория чисел используется для определения некоторых закономерностей в природе, например, в распределении простых чисел в ряде чисел Фибоначчи.

В науке теория чисел применяется в таких областях как физика, экономика, биология и др. Она используется для моделирования различных процессов и явлений, а также для разработки алгоритмов и программных продуктов. Например, теория чисел используется в физике при исследовании свойств кристаллов и квантовых систем, а в биологии — для анализа генома и определения генетических взаимосвязей.

Таким образом, теория чисел — это не просто абстрактная наука, а важный инструмент для решения задач в различных сферах жизни и науки.

Применение теории чисел

Теория чисел – это раздел математики, который изучает свойства и взаимоотношения целых чисел. Многие люди могут подумать, что теория чисел – это просто набор абстрактных и бесполезных знаний. Однако это не так. Теория чисел находит свое применение во многих областях науки и техники.

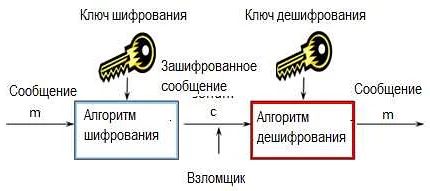
Одним из примеров применения теории чисел является криптография – наука о защите информации. Криптография использует большие простые числа в качестве ключей для шифрования данных. Чем больше число, тем сложнее его факторизовать на простые множители и тем сложнее взломать зашифрованные данные.

Еще одним примером применения теории чисел является комбинаторика – наука о подсчете и перечислении комбинаций и перестановок. Теория чисел используется в комбинаторике для вычисления количества возможных комбинаций и перестановок в различных задачах, например, в теории кодирования и теории графов.

Теория чисел также находит применение в физике. Например, в физике элементарных частиц используется теория чисел для вычисления свойств частиц и прогнозирования результатов экспериментов. Также, в астрономии теория чисел используется для расчета траекторий планет и звезд.

В целом, теория чисел является очень важным разделом математики, который находит свое применение во многих научных областях, а также в различных практических задачах.

Видео по теме:

Теория чисел как отрасль математики

Теория чисел — это отрасль математики, сосредоточенная на исследовании свойств и взаимоотношений между целыми числами. Она имеет широкий спектр применений в науке и технологиях, включая криптографию, коммуникационные системы, статистику, факторизацию больших чисел и многие другие области. Многие из наиболее известных проблем теории чисел, такие как гипотеза Римана и гипотеза Коллатца, по-прежнему остаются нерешенными.

Теория чисел также имеет множество практических применений, включая шифрование данных и защиту информации. Например, RSA криптосистема, которая используется для защиты данных в Интернете, основана на теории чисел и идеи того, что факторизация больших простых чисел сложна.

Теория чисел также имеет большое значение в области коммуникационных систем, таких как системы передачи данных, и в области кодирования. Наборы чисел, используемые в этих системах, часто основываются на свойствах простых чисел и их взаимоотношений.

Наконец, теория чисел играет важную роль в научных исследованиях в различных областях математики, включая геометрию, топологию и теорию групп. В этих дисциплинах теория чисел используется для исследования симметрии и прочности связей между различными математическими объектами.

Криптография и теория чисел

Криптография является наукой, которая использует теорию чисел для защиты информации. Теория чисел используется для разработки криптографических алгоритмов.

Один из наиболее известных примеров криптографического алгоритма, который использует теорию чисел, — это RSA (Rivest-Shamir-Adleman). RSA использует принцип сложности факторизации больших чисел. Даже при использовании компьютерных атак, факторизация большого числа может занять многие годы, даже на суперкомпьютерах.

Другой пример криптографического алгоритма, который использует теорию чисел, — это алгоритм Диффи-Хеллмана. Алгоритм Диффи-Хеллмана используется для создания общего секретного ключа между двумя узлами в открытом канале связи, чтобы обеспечить безопасную связь.

Таким образом, теория чисел играет важную роль в криптографии, которая является необходимой для защиты личной и конфиденциальной информации в интернете.

Использование теории чисел в алгоритмах

Теория чисел — это область математики, которая изучает свойства и отношения между целыми числами. Эта область науки находит свое применение не только в математике, но и в компьютерных науках. Большинство современных алгоритмов используют теорию чисел для решения различных задач.

Простое число — это одно из основных понятий теории чисел. Оно играет важную роль в криптографии и защите информации. Простые числа используются для шифрования данных и создания криптографических ключей. Генерация простых чисел имеет большое значение для создания безопасных систем.

Еще одна область, где теория чисел находит свое применение, это оптимизация алгоритмов. Например, если необходимо исследовать все возможные комбинации паролей, то теория чисел позволяет упростить вычисления, определив, какие числа можно пропустить, не затрагивая необходимых вариантов.

Также теория чисел используется в математических расчетах и алгоритмах поиска простых корней, разложении чисел на множители, проверке чисел на простоту и т.д. Один из таких алгоритмов — алгоритм Эйлера — используется в криптографии для шифрования и расшифровки сообщений.

В целом, можно сказать, что теория чисел является важным инструментом в различных областях, где требуется обработка большого количества числовых данных. Знание основных теорем и алгоритмов позволяет создавать эффективные и безопасные системы.

Теория чисел в криптовалютных технологиях

Криптовалюты, такие как биткоин, основаны на математических алгоритмах и теории чисел. Одним из ключевых элементов криптовалютных технологий является понятие криптографических хешей – математических функций, которые позволяют превратить любой текст или файл в набор цифр фиксированной длины.

Для создания криптовалютных блоков используется алгоритм SHA-256 – хеш-функция, основанная на теории чисел. Этот алгоритм используется для создания цифровой подписи каждого блока, которая подтверждает его подлинность и защищает от изменений.

Одна из задач криптологии – поиск таких парольных функций, которые облегчают генерацию подписей, при этом сложность их взлома и поиска перебором должна быть экспоненциально высокой. В теории чисел существуют подходы к созданию таких функций, например RSA или DSA, которые широко используются в криптографии.

Также теория чисел используется в криптовалютных таких элементов, как алгоритмы доказательства работы (Proof of Work) и доказательства доли собственности (Proof of Stake). Для этих алгоритмов используются комплексные математические функции, которые защищают сеть от атак и обеспечивают децентрализованность криптовалюты.

Использование теории чисел в информационной безопасности

Теория чисел — одна из важнейших областей математики, которая нашла применение во многих сферах, в том числе в информационной безопасности. Ее применение позволяет создавать криптографические алгоритмы, которые служат для защиты информации от несанкционированного доступа.

Одним из применений теории чисел в криптографии является шифрование RSA. Оно основано на принципе факторизации больших чисел. Подобный метод защиты данных очень эффективен, так как факторизация больших чисел является трудоемкой задачей, связанной с большим количеством вычислений. Это значительно усложняет задачу для злоумышленников, которые пытаются расшифровать зашифрованные данные.

Также теория чисел позволяет создавать другие устойчивые криптографические алгоритмы, такие как Эль-Гамаль и Диффи-Хеллман. Кроме того, она используется для определения простых чисел и проверки правильности работы различных криптографических протоколов.

В заключение можно отметить, что применение теории чисел в информационной безопасности является необходимым условием для создания надежной системы защиты данных, которая не будет подвержена атакам злоумышленников.

Примеры использования теории чисел в реальной жизни

Теория чисел имеет широкое применение в нашей жизни. Один из наиболее распространенных примеров использования этой теории — криптография. Криптография — это наука, связанная с созданием кодировок и защитой информации. Теория чисел помогает создавать сложные алгоритмы шифрования и кодировки, которые защищают данные от несанкционированного доступа.

Еще одним примером использования теории чисел является разработка методов для проверки простоты чисел. Эти методы используются во многих областях науки, начиная от управления электронными схемами и заканчивая криптографией.

Теория чисел также используется в разработке алгоритмов для решения задач в области математики и физики. Важную роль играют числа Фибоначчи, используемые для описания многих явлений в природе.

Кроме того, теория чисел находит применение в практических задачах, таких как определение количества простых чисел между двумя заданными числами, вычисление наименьшего общего кратного и наибольшего общего делителя.

Таким образом, теория чисел играет важную роль во многих областях науки и технологии, и ее применение в решении практических задач является неотъемлемой частью различных инженерных проектов.

Теория чисел в современной физике

Одним из основных применений теории чисел в современной физике является шифрование информации. Например, для защиты конфиденциальной информации используются криптосистемы, построенные на основе сложных математических операций с большими простыми числами.

Другим примером использования теории чисел является теория графов, которая находит свое применение в алгоритмах машинного обучения и искусственного интеллекта. Каркас графа можно рассматривать как множество вершин и линий, где вершины соответствуют понятиям, а линии — отношениям между ними.

В физике теория чисел используется для решения сложных математических задач, связанных с теорией струн и многомерными пространствами. Например, числа Фибоначчи можно обнаружить в структуре ряда измерений в теории струн.

Изучение простых чисел, свойств делимости и арифметических функций также является важным аспектом теории чисел в физике. На основе этих знаний ученые разрабатывают математические модели и предсказывают поведение физических систем.

Применение теории чисел в теории графов

Теория чисел и теория графов — это две разные области математики. Однако, теория чисел может быть использована для решения различных задач теории графов, что делает эту двух областей взаимосвязанными.

Одной из важных теорем, связывающих теорию чисел и теорию графов, является теорема Эйлера. Согласно этой теореме, если граф является связным и содержит n вершин и m ребер, то он содержит цикл, проходящий по каждому ребру ровно один раз, тогда и только тогда, когда m = n — 1.

Также, теория чисел может быть использована для определения групп симметрий графов. Например, для неориентированных графов можно определить группу-циклическую группу, связанную с числом вершин и ребер графа. Для ориентированных графов используется группа перестановок вершин и ребер графа.

• Теория чисел может также использоваться для нахождения кратчайших путей в графах. Например, используя алгоритм Эйлера, который базируется на теории чисел, можно находить кратчайшие пути в графах.
• Теория чисел применяется также для нахождения циклов в графах и определения их длины.

Таким образом, теория чисел несет важное значение при решении задач, связанных с теорией графов. Анализ и применение теории чисел может помочь математикам и ученым понимать более глубокие связи между различными областями математики.

Алгоритмы на основе теории чисел

Теория чисел является одной из основных областей математики, применяемых в науке и жизни. Многие алгоритмы основываются на ее принципах.

Например, RSA – криптографический алгоритм, используется для защиты информации. Этот алгоритм основан на сильной математической основе теории чисел. Разными способами этот алгоритм применяют для обеспечения безопасности финансовых транзакций, банковской технологии и мобильных банкоматов.

Другой пример алгоритма на основе теории чисел — это алгоритм Эйлера. Он используется в теории графов, в машинном обучении и в криптографии. Все эти области являются важными для развития науки и технологии.

Одно из главных преимуществ алгоритмов на основе теории чисел — это их высокая эффективность. Благодаря этим алгоритмам, можно эффективно решать сложные задачи и создавать новые технологии, которые помогают улучшать жизнь людей.

В мире науки и технологии практически везде используется теория чисел. Числа и их свойства являются основными элементами этих областей. Алгоритмы на основе теории чисел предоставляют мощные инструменты, которые помогают справляться со сложными задачами и создавать новые технологии, которые улучшают жизнь людей по всему миру.

Теория чисел в математической статистике

Теория чисел играет важную роль в математической статистике, которая занимается изучением данных и выявлением закономерностей в них. Основной задачей математической статистики является описание статистических данных с помощью математических моделей, а также проверка этих моделей на соответствие реальным данным.

Ключевым понятием в математической статистике является вероятность. И здесь теория чисел может быть очень полезна. Например, теория вероятностей включает в себя изучение распределений случайных величин, а также их свойств и параметров. Важными понятиями в этой области являются простые числа и их распределение, теория Мерсенна и прочие.

Еще одной областью, в которой применяется теория чисел, является криптография. Криптография – это наука о методах и средствах защиты информации. Задача криптографии состоит в том, чтобы зашифровать данные таким образом, чтобы в случае несанкционированного доступа к ним, они оставались скрытыми. Здесь теория чисел играет очень важную роль, поскольку она позволяет создавать мощные алгоритмы шифрования.

Также теория чисел используется в других областях математики, таких как теория графов, алгебра и топология. Она также имеет широкое применение в инженерии, физике, экономике и других науках.

Вопрос-ответ:

Что такое теория чисел и каковы ее приложения в жизни и науке?

Теория чисел — это раздел математики, изучающий свойства и взаимосвязи целых чисел. Она находит широкое применение в криптографии, криптовалютах, алгоритмах шифрования, теории кодирования и прочих областях, связанных с защитой информации. Также теория чисел играет важную роль в алгоритмах вычислительной математики, в исследовании свойств простых чисел, в теории графов и многих других областях науки и техники.

Как теория чисел используется при шифровании данных?

Одно из самых широких применений теории чисел — это криптография и алгоритмы шифрования. Например, шифр RSA основан на трудности факторизации больших чисел на простые множители. Этот алгоритм используется для защиты информации при передаче данных в Интернете, при совместимости электронной почты и многих других приложениях, где требуется защита данных от несанкционированного доступа.

Как использование теории чисел влияет на разработку криптовалют?

Теория чисел используется в разработке криптовалют для обеспечения безопасности транзакций и кошельков для хранения виртуальных денег. Один из таких примеров — криптовалюта биткоин, для которой используется алгоритм доказательства выполнения работы (proof-of-work). Этот алгоритм основан на сложных вычислениях, связанных с теорией чисел, и защищен от взлома.

Как теория чисел используется в теории кодирования?

Теория чисел используется в различных алгоритмах кодирования, в том числе для исправления ошибок при передаче данных. Одним из таких примеров является код Рида-Соломона, который используется в цифровой связи и цифровых устройствах для исправления ошибок в данных при передаче. Он основан на числовых манипуляциях над коэффициентами многочлена и поглощает ошибки путем реконструкции исходного сообщения.

Какие задачи решаются при изучении простых чисел в теории чисел?

Изучение простых чисел является одной из основных задач теории чисел. Эта область исследований имеет множество открытых проблем, например, гипотеза Римана. Она важна для разработки алгоритмов шифрования и дешифрования данных, распределенных систем, обработки данных и многих других областей. Изучение простых чисел также необходимо для поиска простых чисел больших размеров, которые используются в различных алгоритмах и задачах науки и техники.

Как теория чисел влияет на анализ поведения финансовых рынков?

Теория чисел используется для анализа финансовых рынков и прогнозирования изменений цен на акции, товары, валюту и другие финансовые инструменты. Один из примеров применения теории чисел в финансовом анализе — это технический анализ. Он основан на принципах теории чисел и исследует исторические данные цен, чтобы найти закономерности и прогнозировать будущие изменения.

Какие задачи решаются в теории графов с применением теории чисел?

Теория графов и теория чисел тесно связаны между собой, и многие вопросы теории графов связаны с числовыми свойствами графов. Например, задача о гамильтоновом пути в графе — это одна из классических задач теории графов, которая может быть решена с применением теории чисел. Кроме того, теория чисел в теории графов используется для изучения свойств графовых последовательностей, различных индексов графа, его экспандерных свойств и др.