Что значит хвост по математике

Хвост по математике – это остаточная часть числа или функции после того, как основная часть уже была обработана или учтена. Узнайте, как можно использовать хвосты в математике для решения задач и анализа данных.

В математике понятие «хвост» используется для обозначения остаточной части ряда или последовательности. В контексте числовых рядов хвостом называют ту часть ряда, которая остается после отбрасывания определенного числа начальных членов.

Хвост может быть полезен при анализе сходимости ряда или последовательности. Выделение хвоста позволяет сосредоточиться на его остаточной части и провести более детальное исследование, например, вычислить его сумму или определить его свойства.

Вычисление хвоста ряда или последовательности зависит от его определения и свойств. Для некоторых рядов существуют формулы или методы, которые позволяют вычислить хвост аналитически. В других случаях может потребоваться численное решение или использование специальных алгоритмов.

Например, при анализе геометрической прогрессии можно вычислить сумму первых n членов и затем вычислить остаток суммы, чтобы получить хвост ряда.

Таким образом, понимание понятия «хвост» в математике и умение вычислять его позволяет более глубоко исследовать ряды и последовательности, а также применять их в различных областях, где требуется анализ и оптимизация числовых данных.

Определение хвоста в математике

В математике хвост часто используется в контексте последовательностей чисел или рядов. Он представляет собой оставшуюся часть последовательности или ряда после отбрасывания определенного числа элементов.

Хвост можно представить в виде бесконечного множества элементов или как конечную часть последовательности. В зависимости от контекста, хвост может быть определен как остаток последовательности или ряда после определенного элемента или группы элементов.

Вычисление хвоста может быть полезным, когда требуется анализировать оставшуюся часть последовательности или ряда, или когда нужно определить, какие элементы исключены из общего набора данных.

Хвост в математике играет важную роль в различных областях, включая теорию вероятности, статистику, анализ и дискретную математику. Понимание понятия хвоста позволяет более глубоко изучать эти области и решать сложные математические задачи.

Видео по теме:

Как вычислить хвост

1. Выбрать число, от которого будет производиться деление.
2. Выбрать число, которым будет производиться деление.
3. Выполнить деление и получить результат.
4. Определить остаток от деления, который и будет являться хвостом.

Пример:

• Дано число 15.
• Установлено, что число для деления равно 7.
• Выполняем деление: 15 / 7 = 2, остаток 1.
• Остаток 1 является хвостом.

Таким образом, хвост — это остаток от деления числа на другое число и может быть вычислен с помощью деления и определения остатка.

Формула для вычисления хвоста

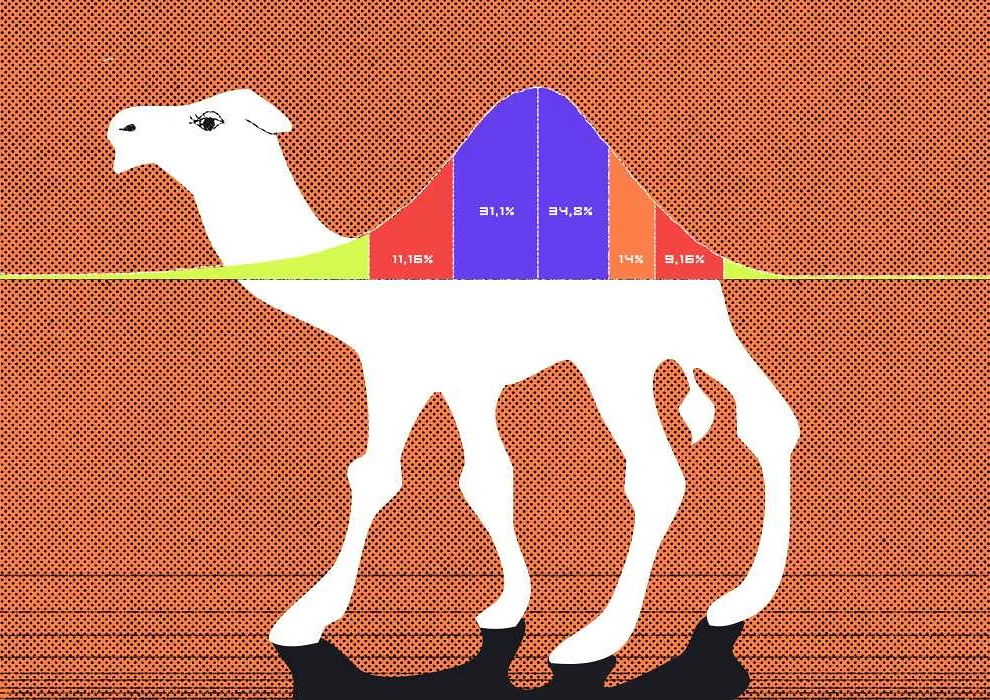
ФормулаПримерРезультат

хвост = число % делитель

17 % 5

2

В этой формуле число – это число, у которого мы хотим найти хвост, а делитель – число, на которое мы хотим разделить число для вычисления хвоста. Оператор % возвращает остаток от деления числа на делитель.

В примере выше, при делении числа 17 на 5, получается остаток равный 2. Этот остаток и является хвостом.

Примеры использования хвоста

Пример 1: Округление до ближайшего целого числа.

Допустим, нам необходимо округлить число 4.8 до ближайшего целого числа. Для этого мы смотрим на хвост числа, который в данном случае равен 8. Так как хвост больше или равен 5, мы прибавляем 1 к целой части числа. Итого, 4.8 округляется до 5.

Пример 2: Округление до определенного количества знаков после запятой.

Допустим, нам необходимо округлить число 3.14159 до двух знаков после запятой. Мы смотрим на хвост числа, который в данном случае равен 9. Так как хвост больше или равен 5, мы увеличиваем предыдущий разряд на 1. Итого, 3.14159 округляется до 3.14.

Пример 3: Округление до ближайшего десятка.

Допустим, нам необходимо округлить число 27 до ближайшего десятка. Мы смотрим на хвост числа, который в данном случае равен 7. Так как хвост больше или равен 5, мы прибавляем 1 к десяткам. Итого, 27 округляется до 30.

Примеры использования хвоста в математике помогают более точно округлять числа и получать более точные результаты в вычислениях.

Пример 1: Вычисление хвоста в задаче с графиком

Для наглядного представления и анализа данных в математике часто используются графики. Рассмотрим пример задачи, в которой необходимо вычислить хвост по графику функции.

Пусть дан график функции y = f(x), представленный на координатной плоскости. Нам нужно найти хвост, то есть часть графика функции, которая находится за определенной точкой или отрезком.

Для начала определим точку или отрезок, после которого начинается хвост. Обозначим эту точку или отрезок как P. В нашем примере возьмем точку P(3, 2).

Далее, построим прямую, проходящую через точку P и совпадающую с графиком функции до точки P. Эта прямая будет задавать начало хвоста.

Затем, проведем перпендикулярную прямую к оси абсцисс в точке P. Эта прямая будет задавать направление хвоста.

Для определения конца хвоста, можно продолжить построенный перпендикуляр до пересечения с графиком функции.

Таким образом, хвостом в данной задаче будет являться часть графика функции, которая находится после точки P и ограничена прямой, проведенной через P и перпендикулярной оси абсцисс.

Пример 2: Применение хвоста в статистике

Хвост в статистике часто используется для проверки гипотез о распределении данных. Рассмотрим следующий пример.

Представим, что у нас есть выборка из 100 значений, которые предположительно должны следовать нормальному распределению. Мы хотим проверить, является ли эта выборка действительно нормально распределенной.

Для этой цели мы можем использовать тест Шапиро-Уилка, который позволяет проверить нулевую гипотезу о нормальности данных. Если p-значение, полученное в результате теста, меньше уровня значимости (обычно 0,05), мы отвергаем нулевую гипотезу и делаем вывод, что данные не следуют нормальному распределению.

Однако, в некоторых случаях, данные могут быть нормально распределены в основной части (так называемая «тело» распределения), но иметь отклонения в хвостах. Используя тест Шапиро-Уилка, мы можем не обнаружить эти отклонения и сделать неправильный вывод о нормальности данных.

Для того чтобы обнаружить такие отклонения в хвостах распределения, можно использовать альтернативный тест — тест Лиллиефорса. Он также проверяет нулевую гипотезу о нормальности данных, но более чувствителен к отклонениям в хвостах распределения.

Таким образом, в данном примере применение хвоста в статистике позволяет более точно проверить гипотезу о нормальности данных и обнаружить отклонения, которые могут быть незаметны при использовании только основной части распределения.

Тестp-значениеВывод

Тест Шапиро-Уилка	0.073	Не отвергаем нулевую гипотезу
Тест Лиллиефорса	0.032	Отвергаем нулевую гипотезу

На основании результатов тестов, мы делаем вывод, что данные не следуют нормальному распределению и имеют отклонения в хвостах.

Практические рекомендации

Вычисление хвоста в математике может быть сложным процессом, и вот несколько практических рекомендаций, которые могут помочь вам справиться с этой задачей:

1. Изучите основные понятия и определения, связанные с хвостом. Это поможет вам понять, как он работает и какие методы можно использовать для его вычисления.
2. Пользуйтесь математическими таблицами и формулами. Они предоставят вам необходимую информацию для выполнения вычислений.
3. Используйте компьютерные программы или калькуляторы для выполнения сложных вычислений. Это позволит вам сэкономить время и уменьшить вероятность ошибок.
4. Практикуйтесь в решении различных задач, связанных с хвостом. Чем больше практики вы получите, тем лучше вы справитесь с вычислениями в реальных ситуациях.
5. Обратитесь к учебным пособиям и онлайн-курсам по математике. Они предоставят вам дополнительные материалы и задачи для тренировки.

Следуя этим практическим рекомендациям, вы сможете разобраться с хвостом в математике и успешно выполнить его вычисление.

Как использовать хвост в повседневной жизни

Хвост, или остаток, в математике представляет собой остаток от деления одного числа на другое. Хвост может быть полезным в повседневной жизни во многих ситуациях.

Одним из примеров использования хвоста является деление большого количества предметов на группы. Например, если у вас есть 100 конфет и вы хотите разделить их между 10 друзьями равномерно, вы можете использовать хвост, чтобы узнать сколько конфет будет у каждого друга и сколько конфет останется. Для этого нужно разделить 100 на 10 и посмотреть на хвост — он покажет, сколько конфет останется после равномерного распределения.

Другим примером использования хвоста является вычисление остатка от сдачи при покупке. Например, если вы покупаете товар стоимостью 1500 рублей и платите купюрой в 2000 рублей, вы можете использовать хвост, чтобы узнать сколько сдачи вам вернут и какие купюры будут использованы. Для этого нужно вычесть стоимость товара из суммы, которую вы отдали, и посмотреть на хвост — он покажет, сколько рублей останется после выдачи сдачи.

Таким образом, хвост в математике имеет практическое применение в повседневной жизни. Он позволяет решать различные задачи, связанные с делением и остатками, и помогает нам легче справляться с математическими вычислениями.

Вопрос-ответ:

Что такое хвост в математике?

Хвост в математике — это часть распределения вероятностей или функции, которая находится за определенной границей.

Как вычислить хвост в математике?

Для вычисления хвоста в математике нужно знать границу, за которой находится хвост, и функцию распределения или вероятности. Затем нужно проинтегрировать функцию или подсчитать вероятность от границы до бесконечности.

Как определить границу хвоста в математике?

Граница хвоста в математике определяется на основе контекста задачи или распределения. Обычно граница выбирается так, чтобы за нее попадало небольшое количество наблюдений или вероятностей.

Какие применения у хвоста в математике?

Хвост в математике может использоваться для анализа экстремальных событий, выбросов или редких случаев. Также хвост может помочь исследователям определить, какие значения являются необычными или статистически значимыми.