Что такое эпсилон в математике

Эпсилон в математике — это символ, который используется для обозначения очень малого числа или бесконечно малой величины. В математических выражениях он указывает на приближение к нулю или бесконечно малое отклонение. Понимание эпсилона важно для понимания понятий пределов, непрерывности функций и решения математических задач.

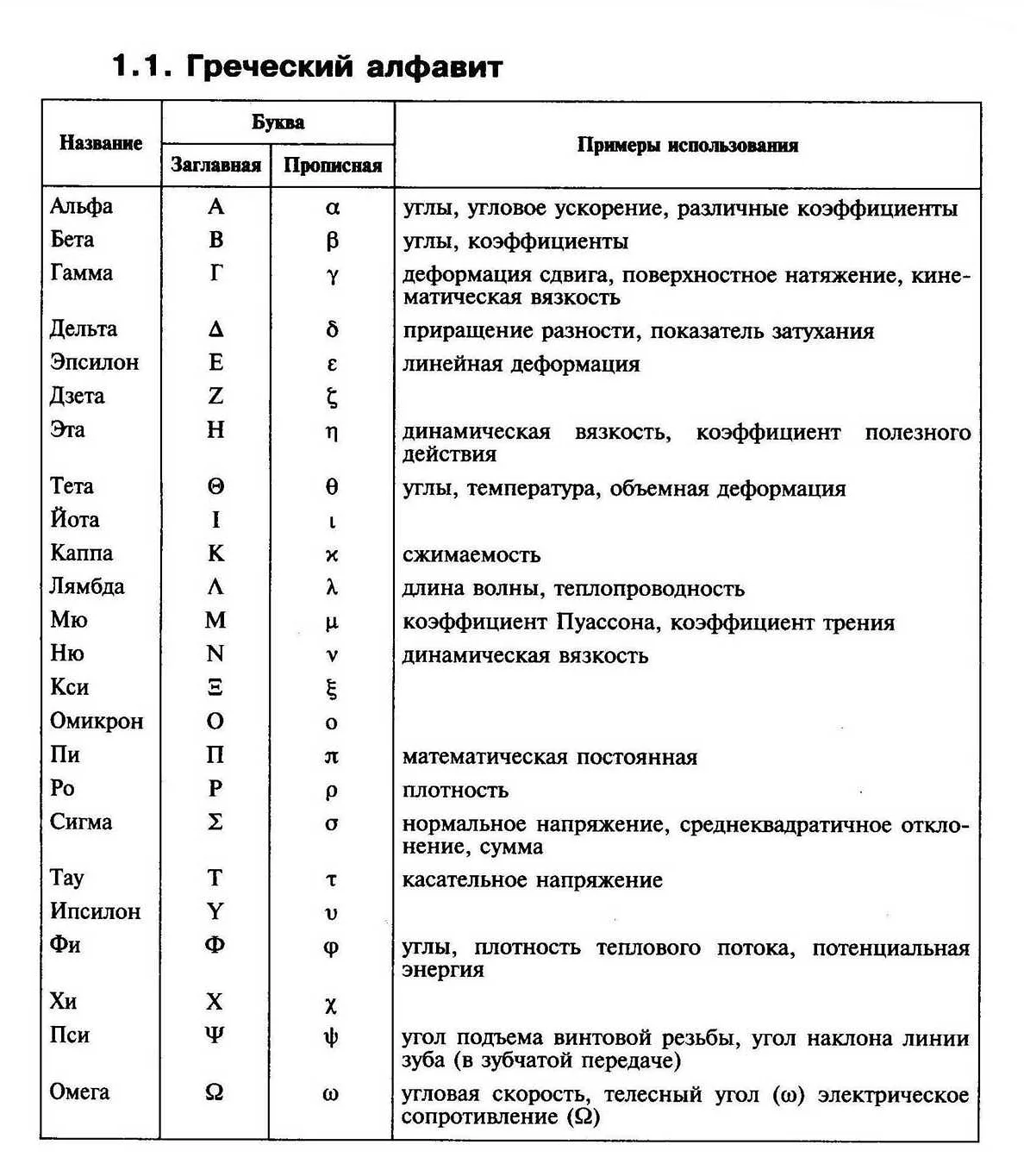
Эпсилон — это один из важнейших символов, используемых в математике. Он является буквой греческого алфавита, обозначается символом ε и используется для обозначения очень малых чисел или величин. Как правило, эпсилон используется в контексте пределов и приближений. В математических выражениях эпсилон может принимать различные значения в зависимости от задачи и условий задачи.

Одно из свойств эпсилон заключается в том, что оно может быть очень малым, но не равным нулю. Это позволяет использовать эпсилон для описания точности вычислений или измерений. Например, если мы говорим о пределе функции в точке, то мы можем сказать, что предел равен некоторому значению L, если для любого положительного числа эпсилон найдется такое положительное число дельта, что для всех x, отличных от точки предела, расстояние между значением функции и L будет меньше эпсилон.

Эпсилон также может использоваться для задания условий сходимости или ограниченности последовательности или ряда. Например, если для любого положительного числа эпсилон найдется такой номер n, начиная с которого все элементы последовательности будут находиться внутри отрезка [L — эпсилон, L + эпсилон], то говорят, что последовательность сходится к L.

Эпсилон имеет широкое применение в различных областях математики, физики, экономики и других наук. Он позволяет формализовать и описать понятия точности, предела, сходимости и многие другие. Знание и понимание эпсилонов и их свойств является необходимым для успешного изучения и применения различных математических концепций и методов.

Эпсилон в математике: определение, свойства и применение

Определение эпсилон-окрестности: если ε — положительное число, то эпсилон-окрестностью точки a называется интервал (a-ε, a+ε), состоящий из всех точек на числовой прямой, расположенных на расстоянии меньше, чем ε от точки a.

Свойства эпсилон:

1. Эпсилон может быть выбрано произвольно малым, но положительным числом.
2. Эпсилон используется для формализации понятия предела функции. Например, предел функции f(x) при x стремящемся к a обозначается как f(x) -> L при x -> a, где L — это предельное значение функции, а эпсилон используется для определения того, насколько близко значения функции должно быть к L.
3. Эпсилон также используется в определении непрерывности функции. Функция считается непрерывной в точке a, если для любого ε > 0 существует δ > 0 такое, что если |x — a| < δ, то |f(x) — f(a)| < ε.

Применение эпсилон в математике широко встречается в различных областях, включая анализ, теорию множеств, теорию вероятности и другие. Он играет важную роль в точном определении и рассмотрении различных математических понятий.

Что такое эпсилон в математике?

Эпсилон используется, например, при определении предела функции или последовательности. Когда мы говорим, что предел функции f(x) при x стремится к некоторому значению a равен L, мы можем написать это в виде:

limx→a f(x) = L

Где lim — обозначение предела, x→a — стремление аргумента x к значению a, f(x) — сама функция, L — предельное значение.

Теперь мы можем сформулировать определение предела функции с использованием эпсилон:

Для любого положительного числа эпсилон, существует такое положительное число дельта, что если x находится в некоторой окрестности a (но не равно a), то f(x) лежит в окрестности L (но не обязательно равно L). Математически это можно записать как:

Для любого положительного числа эпсилон, существует положительное число дельта, такое что если 0 < |x — a| < дельта, то |f(x) — L| < эпсилон.

Такое определение позволяет нам формализовать понятие предела и проводить точные математические рассуждения о поведении функций.

Понятие эпсилон в математике

В математике термин «эпсилон» часто используется для обозначения малого положительного числа, которое может быть сколь угодно малым, но все равно положительным. Значение этого числа может быть произвольным, но оно всегда стремится к нулю.

Эпсилон широко применяется в математических определениях, свойствах и доказательствах. Например, в определении предела функции, эпсилон используется для формализации понятия «близости» одной величины к другой. Если предел функции равен некоторому числу L, то для любого положительного числа эпсилон существует такое положительное число дельта, что все значения функции, лежащие в проколотой окрестности точки, отличаются от L меньше, чем на эпсилон.

В математическом анализе эпсилон используется для доказательства существования и единственности пределов и решений уравнений. Он также используется для доказательства сходимости и расходимости рядов и последовательностей.

Свойства эпсилонПрименение

Эпсилон может быть произвольным положительным числом	Определение предела функции
Значение эпсилон стремится к нулю	Доказательство существования и единственности пределов и решений
Эпсилон используется для формализации понятия «близости»	Доказательство сходимости и расходимости рядов и последовательностей

Свойства эпсилон в математике

Свойства эпсилон в математике включают:

1. Эпсилон может быть выбран произвольно, однако его значение обычно зависит от конкретной задачи или контекста.
2. Чем меньше значение эпсилон, тем точнее будет результат вычислений или приближений.
3. Если значение разности двух чисел меньше эпсилона, то эти числа считаются равными.
4. Эпсилон может использоваться для определения предела функции или последовательности. Если разность между значениями функции или элементами последовательности становится меньше эпсилона, то можно говорить о приближении к пределу.
5. Эпсилон часто используется для оценки ошибок при численных вычислениях. Если разность между точным значением и приближенным значением меньше эпсилона, то приближенное значение считается достаточно точным.

Эпсилон является одним из важных понятий в математике, которое играет важную роль во многих областях, включая анализ, численные методы и теорию вероятностей.

Применение эпсилон в математике

Во-первых, эпсилон используется для определения пределов функций. При изучении пределов функций в математике, эпсилон играет роль «погрешности» или «точности». Говоря простыми словами, предел функции f(x) равен L, если для любого положительного числа эпсилон существует положительное число дельта такое, что для всех x, лежащих в окрестности точки a (за исключением самой точки a), выполнено неравенство |f(x) — L| < эпсилон.

Во-вторых, эпсилон используется в определении равенства между двумя числами. Говорят, что два числа a и b равны, если их разность |a — b| меньше любого положительного числа эпсилон. Другими словами, для любого положительного числа эпсилон выполняется неравенство |a — b| < эпсилон.

В-третьих, эпсилон используется в определении непрерывности функций. Говорят, что функция f(x) непрерывна в точке a, если для любого положительного числа эпсилон существует положительное число дельта такое, что для всех x, лежащих в окрестности точки a, выполнено неравенство |f(x) — f(a)| < эпсилон.

Таким образом, эпсилон играет важную роль в математике и используется для определения точности, пределов, равенства и непрерывности.

Значение эпсилон в математике

Значение эпсилон является ключевым понятием в анализе и численных методах. В анализе эпсилон используется для формулировки определений предела функции, непрерывности, производной и других важных понятий. Например, предел функции f(x) при x стремящемся к a определяется следующим образом:

Определение:limf(x)= L,еслидля каждогоε > 0существуетδ > 0,такое чтоесли0 < |x — a| < δ,то|f(x) — L| < ε.

В численных методах эпсилон используется для контроля точности вычислений. Например, часто требуется найти приближенное значение корня уравнения с заданной точностью. В этом случае эпсилон используется для определения условия остановки численного метода. Операция обычно прекращается, когда достигается приближенное значение корня, которое удовлетворяет неравенству:

|f(x)| < ε,

где f(x) — функция, корнем которой является x.

Таким образом, значение эпсилон играет критическую роль в математике, позволяя формулировать определения, контролировать точность вычислений и делать выводы о свойствах объектов и функций.

Импорт эпсилон в математике

В языке программирования Python, например, вы можете импортировать эпсилон из модуля math следующим образом:

from math import epsilon

После этого вы можете использовать переменную epsilon для представления эпсилона в своих вычислениях или сравнениях чисел с плавающей точкой.

Импорт эпсилона позволяет вам точно контролировать точность вычислений и избегать ошибок округления. Он особенно полезен при работе с числами, которые могут иметь малые отклонения от ожидаемых значений.

Помимо языка программирования Python, импорт эпсилона возможен также в других математических пакетах и средах разработки. Например, в языке MATLAB вы можете использовать функцию eps для получения значения эпсилона.

Важно помнить, что значение эпсилона может отличаться в зависимости от используемого пакета или языка программирования. Поэтому перед использованием эпсилона в своих вычислениях, рекомендуется ознакомиться с документацией или руководством к соответствующему пакету или языку.

Эпсилон в математике для начинающих

В математических определениях и уравнениях, эпсилон используется, чтобы указать, что значение или разность между двумя числами очень маленькая и может быть близка к нулю. Например, если мы говорим, что число «х» стремится к числу «а», то мы можем записать это как:

х → а, при х → 0

Здесь символ «→» означает «стремится к», а «0» — это значение, к которому «х» стремится. В этом случае, эпсилон (ε) может быть использован для определения, насколько близко «х» может быть к «а». Если мы говорим, что «х» стремится к «а» с точностью до эпсилон, мы можем записать это как:

х → а, при х → 0, с точностью до ε

Эпсилон также используется в математических неравенствах, чтобы указать, что разность между двумя числами меньше или равна некоторому очень маленькому числу. Например:

Математическое неравенствоОписание

|х — а| ≤ ε	Разность между «х» и «а» меньше или равна эпсилон
|х — а| < ε	Разность между «х» и «а» меньше эпсилон

В этих неравенствах, символ «|» обозначает абсолютную разность между двумя числами. Эпсилон указывает на то, что разность между числами очень маленькая или близка к нулю.

Использование эпсилон в математике позволяет нам формально определить понятие предела и непрерывности функций. Он также используется во многих других областях математики, таких как дифференциальное и интегральное исчисление, теория вероятностей и других.

Итак, эпсилон (ε) является важным символом в математике, который помогает нам формализовать и работать с понятием очень малых чисел и бесконечно малых величин.

Вопрос-ответ:

Что такое эпсилон в математике?

В математике эпсилон – это малая положительная величина, которая используется для описания бесконечно малых изменений или отклонений в математических выражениях. Она часто используется для определения пределов функций, сходимости рядов и других математических концепций.

Какие свойства имеет эпсилон в математике?

Эпсилон обладает несколькими свойствами. Во-первых, эпсилон всегда положительный. Во-вторых, он может быть произвольно малым, но всегда больше нуля. Также, эпсилон используется для описания бесконечно малых изменений или отклонений в математических выражениях, и его значение зависит от контекста, в котором он используется.

В каких случаях эпсилон используется в математике?

Эпсилон используется в различных областях математики. Он может быть использован для определения пределов функций, сходимости рядов, точности численных вычислений и многих других математических концепций. Эпсилон позволяет нам описывать и анализировать бесконечно малые изменения или отклонения в математических выражениях.

Как эпсилон помогает определить пределы функций?

Эпсилон используется в определении пределов функций, чтобы формализовать их сходимость. Конкретно, для заданной функции f(x) и предела L, мы можем сказать, что предел существует, если для любого положительного числа эпсилон, существует положительное число дельта, такое что, если x находится в окрестности точки a, то f(x) будет находиться в окрестности точки L, с точностью до эпсилон.

Как эпсилон используется для оценки точности численных вычислений?

При численных вычислениях, эпсилон используется для оценки точности результата. Например, если мы хотим вычислить значение функции с заданной точностью, мы можем использовать эпсилон как критерий остановки для итераций вычислений. Если разница между текущим и предыдущим значением функции меньше, чем эпсилон, мы можем считать, что мы достигли желаемой точности и остановить вычисления.

Зачем нужно понимать, что такое эпсилон в математике?

Понимание понятия эпсилон в математике важно для решения различных математических задач, особенно в анализе и теории вероятностей. Эпсилон обозначает очень малое положительное число, которое используется в определении предела функции или последовательности. Понимание эпсилон позволяет более точно формулировать и доказывать математические утверждения.

Как определить эпсилон в математике?

Эпсилон в математике определяется как положительное число, которое может быть произвольно малым, но всегда больше нуля. Точное значение эпсилона зависит от конкретной задачи или определения, в котором оно используется. Обычно эпсилон обозначается греческой буквой ε.

Примеры использования эпсилон в математике

1. Определение предела. Эпсилон используется при определении предела функции. Математически, если для каждого положительного числа ε существует положительное число δ такое, что для всех x, для которых 0 < |x — a| < δ, выполняется |f(x) — L| < ε, то говорят, что предел функции f(x) при x стремящемся к a равен L, и записывают это как limx→a f(x) = L.

2. Точность вычислений. В численных методах, эпсилон используется для определения точности вычислений. Если разница между ожидаемым и полученным результатом меньше заданного значения ε, то считается, что вычисления достаточно точны.

3. Границы и неравенства. Эпсилон также используется при формулировании границ и неравенств. Например, в теории вероятностей, можно установить, что вероятность события A больше, чем ε, где ε — некоторое малое положительное число.

4. Точность аппроксимации. Эпсилон используется для оценки точности аппроксимации. Если разница между истинным значением и аппроксимацией меньше ε, то аппроксимация считается достаточно точной.

5. Условия сходимости. Эпсилон используется в условиях сходимости рядов и последовательностей. Например, ряд сходится, если для каждого положительного числа ε существует натуральное число N такое, что для всех n ≥ N выполняется |an — L| < ε.

Все эти примеры показывают, что эпсилон играет важную роль в математике и помогает определить точность, пределы, границы и условия сходимости различных математических объектов.

Видео по теме: