Что такое компоненты в математике 3 класс
Содержимое
- 1 Что такое компоненты в математике 3 класс
- 1.1 Определение компонентов в математике 3 класс
- 1.2 Видео по теме:
- 1.3 Основные понятия
- 1.4 Примеры компонентов
- 1.5 Значение компонентов в математике
- 1.6 Как определить компоненты в задаче
- 1.7 Использование компонентов в решении задач
- 1.8 Роль компонентов в математическом анализе
- 1.9 Задачи, связанные с компонентами
- 1.10 Вопрос-ответ:
- 1.10.0.1 Какие основные понятия связаны с компонентами в математике 3 класс?
- 1.10.0.2 Что такое компоненты числа в математике 3 класс?
- 1.10.0.3 Как вычислить компоненты числа?
- 1.10.0.4 Какие операции можно выполнять с компонентами числа?
- 1.10.0.5 Как использовать компоненты числа в решении математических задач?
Компоненты в математике 3 класс — это числа или выражения, которые используются для создания более сложных математических операций. В данной статье рассматривается понятие компонентов и их применение при решении простых математических задач в третьем классе.
В математике 3 класса одним из основных понятий являются компоненты. Компоненты — это числа, которые складываются или вычитаются друг с другом. Понимание компонентов помогает ученикам разбираться в арифметических операциях и решать задачи.
Основными компонентами являются слагаемые и разности. Слагаемые — это числа, которые складываются. Разности — это числа, которые вычитаются друг из друга. Например, в задаче «На столе лежат 5 книг и 3 ручки. Сколько всего предметов на столе?» число 5 и число 3 являются слагаемыми, так как они складываются. Результатом сложения будет число 8 — это сумма слагаемых.
Компоненты могут быть представлены в виде чисел, слов или предметов. Например, в задаче «На столе лежат 3 яблока и 2 груши. Сколько всего фруктов на столе?» число 3 и число 2 являются слагаемыми, так как они складываются.
Разности также являются компонентами. Например, в задаче «На столе лежат 8 книг, а потом на стол положили еще 3 книги. Сколько стало книг на столе?» число 8 и число 3 являются компонентами, так как их вычитают друг из друга. Результатом вычитания будет число 5 — это разность компонентов.
Определение компонентов в математике 3 класс
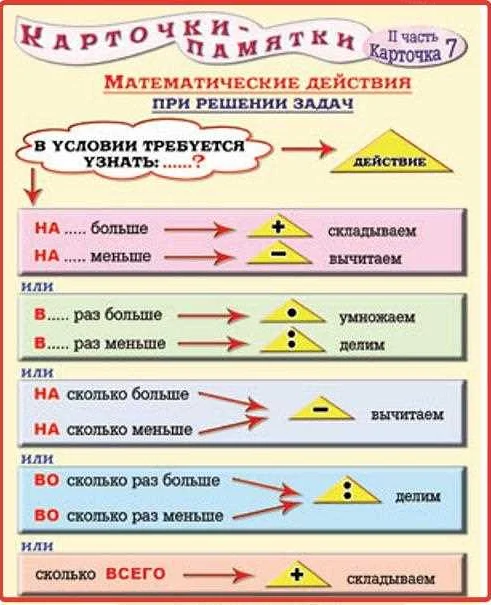
Компоненты могут быть различными и сочетаться между собой. Они могут быть числами от 0 до 9 и использоваться для составления других чисел. Например, в числе 347, компонентами являются числа 3, 4 и 7.
Основными математическими операциями, где используются компоненты, являются сложение, вычитание, умножение и деление. Для выполнения этих операций дети должны знать компоненты чисел и уметь их правильно применять.
Изучение компонентов в математике 3 класс – это первый шаг к пониманию числовых операций и развитию математического мышления у детей. Понимая, что числа состоят из компонентов, дети смогут легче выполнять различные математические задачи и решать проблемы.
Видео по теме:
Основные понятия
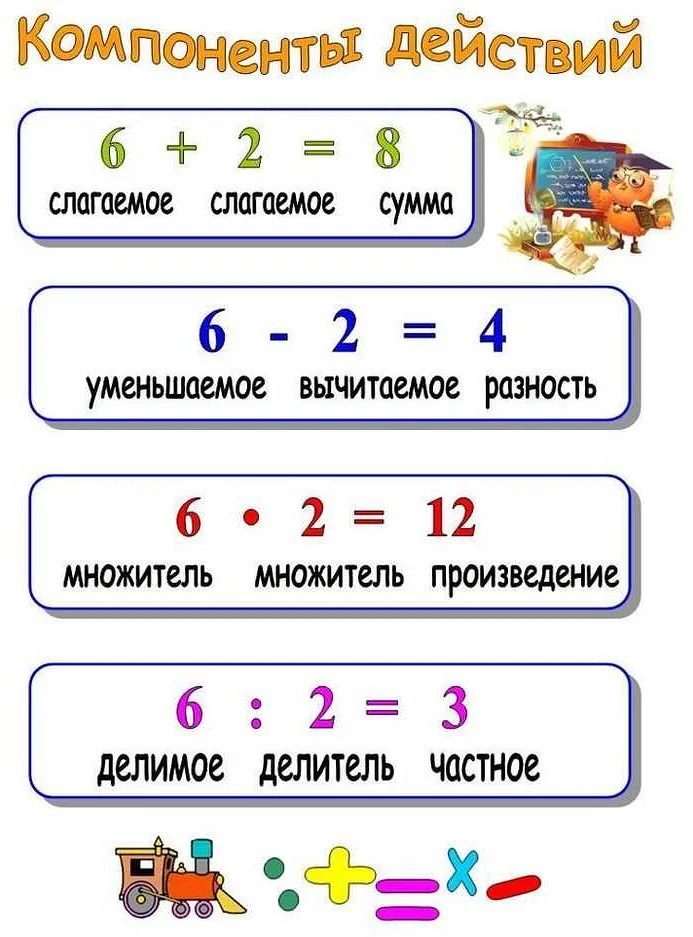
- Целая часть числа: это самое большое целое число, которое меньше данного числа. Например, целая часть числа 5,7 равна 5.
- Дробная часть числа: это часть числа, которая находится после запятой. Например, дробная часть числа 5,7 равна 0,7.
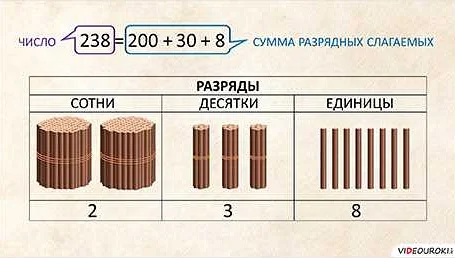
- Разряды числа: числа записываются с помощью разрядов, которые указывают на позицию каждой цифры в числе. Например, в числе 5432 разряды это тысячи, сотни, десятки и единицы.
- Разрядные числа: это числа, которые состоят только из одного разряда. Например, разрядные числа от 0 до 9.
Понимание этих основных понятий поможет ученикам лучше понять структуру чисел и работать с ними в математике.
Примеры компонентов
В математике, компоненты могут быть представлены различными способами. Ниже приведены несколько примеров компонентов:
- Компоненты числа 27:
- Единицы — 7
- Десятки — 2
- Сотни — 0
- Компоненты числа 456:
- Единицы — 6
- Десятки — 5
- Сотни — 4
- Компоненты числа 891:
- Единицы — 1
- Десятки — 9
- Сотни — 8
В каждом числе имеется определенное количество компонентов, которые представляют его разряды. Понимание компонентов числа помогает в изучении и выполнении различных математических операций.
Значение компонентов в математике
Числовые компоненты — это конкретные числа, которые используются в вычислениях. Например, в выражении «3 + 2», числовые компоненты это 3 и 2.
Переменные компоненты — это символы, которые представляют неизвестные значения. Они используются для обозначения неизвестных или переменных в выражениях. Например, в выражении «x + 5», переменная компонента это x.
Операционные компоненты — это знаки или операторы, которые указывают, какие математические операции нужно выполнить. Они могут быть сложением (+), вычитанием (-), умножением (*), делением (/) и другими. Например, в выражении «2 + 3», операционная компонента это +.
Значение компонентов в математике определяется их взаимодействием и порядком выполнения операций. Операции выполняются последовательно, сначала учитывая скобки, затем умножение и деление, а затем сложение и вычитание.
Например, в выражении «3 + 2 * 4», сначала выполняется операция умножения (2 * 4), а затем сложение (3 + 8), что дает итоговое значение 11.
Понимание компонентов в математике помогает разбираться в сложных выражениях и правильно выполнять вычисления.
Как определить компоненты в задаче

Компоненты могут представлять собой различные величины, объекты, числа или действия, которые присутствуют в задаче и являются важными для ее решения. Они могут быть как известными, так и неизвестными величинами.
Примеры компонентов в задаче:
- Известная длина отрезка.
- Неизвестное число, которое нужно найти.
- Известная формула или правило, которое нужно применить для решения задачи.
- Известные значения других величин, которые можно использовать в расчетах.
- Действия или операции, которые нужно выполнить для получения результата.
Определение компонентов в задаче помогает структурировать информацию и понять, какие данные и действия нужно использовать для решения задачи. Это важный шаг при решении математических задач, так как позволяет выделить основные элементы и сосредоточиться на них.
Использование компонентов в решении задач

Когда мы решаем задачу, нам часто приходится работать с большими числами. Использование компонентов позволяет нам разбить эти числа на более мелкие части, чтобы мы могли их легче обработать. Например, при сложении чисел мы можем разложить каждое число на сотни, десятки и единицы, а затем сложить соответствующие компоненты вместе.
Компоненты могут быть использованы также при вычитании, умножении и делении. Они помогают нам разбить сложные операции на более простые шаги, что делает решение задачи более понятным и удобным.
Например, если мы должны вычислить произведение двух трехзначных чисел, мы можем разложить каждое число на сотни, десятки и единицы, а затем перемножить соответствующие компоненты. Это позволяет нам упростить задачу и избежать ошибок при умножении больших чисел.
Использование компонентов также позволяет нам проводить проверку результата. Если мы сложили или умножили компоненты правильно, мы можем легко проверить, что наше окончательное число совпадает с исходными числами.
Таким образом, использование компонентов является важным инструментом при решении математических задач. Они помогают нам легче работать с большими числами, разбивая их на более простые части, и упрощают вычисления и понимание математических операций.
Роль компонентов в математическом анализе

Компоненты в математическом анализе могут быть различными: числами, переменными, операторами и функциями. Например, в выражении 3x + 2y + 5 компонентами являются числа 3, 2 и 5, переменные x и y, а также операторы + и *. Каждый из этих компонентов имеет свою роль и значение в задаче.
Компоненты позволяют анализировать и изучать математические объекты более подробно. Например, если мы имеем функцию f(x) = 2x^2 — 3x + 1, компоненты этой функции позволяют нам определить, как меняется значение функции при изменении значения переменной x. Мы можем выделить компоненты 2x^2, -3x и 1, и изучить их влияние на общий график функции.
Кроме того, компоненты позволяют решать сложные математические задачи. Если мы имеем систему уравнений, состоящую из нескольких компонентов, мы можем анализировать каждое уравнение отдельно и находить решение для каждой переменной. После этого мы можем объединить решения и получить общее решение системы.
Таким образом, компоненты играют важную роль в математическом анализе. Они помогают упростить вычисления, изучать свойства математических объектов и решать сложные задачи. Понимание роли компонентов поможет ученикам лучше разбираться в математических концепциях и развивать аналитическое мышление.
Задачи, связанные с компонентами
1. Сложение компонентов:
Ученикам предлагается сложить два компонента, чтобы получить их сумму. Например, если первый компонент равен 5, а второй компонент равен 3, то сумма будет равна 8.
2. Вычитание компонентов:
Ученикам предлагается вычесть один компонент из другого, чтобы получить разность. Например, если первый компонент равен 7, а второй компонент равен 4, то разность будет равна 3.
3. Определение компонента:
Ученикам предлагается найти один из компонентов, если известна сумма и другой компонент. Например, если сумма двух компонентов равна 9, а один из компонентов равен 4, то второй компонент можно определить, вычтя из суммы известный компонент.
4. Задачи на составление компонентов:
Ученикам предлагается составить компоненты, зная сумму и один из компонентов. Например, если сумма двух компонентов равна 12, а один из компонентов равен 8, то второй компонент можно определить, вычтя из суммы известный компонент.
Решение таких задач помогает ученикам развивать навыки работы с компонентами, понимать основные понятия и развивать математическое мышление.
Вопрос-ответ:
Какие основные понятия связаны с компонентами в математике 3 класс?
Основные понятия, связанные с компонентами в математике 3 класса, включают в себя представление числа в виде суммы его компонентов, нахождение компонентов числа, операции сложения и вычитания компонентов.
Что такое компоненты числа в математике 3 класс?
Компоненты числа — это числа, которые при сложении дают данное число. Например, компоненты числа 7 — это 3 и 4, так как 3 + 4 = 7.
Как вычислить компоненты числа?
Чтобы вычислить компоненты числа, нужно разбить это число на две или более части таким образом, чтобы их сумма равнялась данному числу. Например, чтобы найти компоненты числа 9, можно разделить его на 5 и 4, так как 5 + 4 = 9.
Какие операции можно выполнять с компонентами числа?
С компонентами числа можно выполнять операции сложения и вычитания. Например, если компоненты числа 8 — это 2 и 6, то можно сложить их: 2 + 6 = 8, или вычесть: 6 — 2 = 4.
Как использовать компоненты числа в решении математических задач?
Компоненты числа могут быть полезны при решении задач, связанных с разбиением числа на две или более части. Например, если задача состоит в том, чтобы разделить 10 яблок между двумя детьми поровну, можно использовать компоненты числа 10 (например, 5 и 5) для решения задачи.


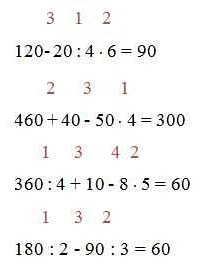
Очень интересная статья! Я, как мама третьеклассника, часто сталкиваюсь с тем, что моему ребенку сложно разобраться в математике. Я читала много материалов на эту тему, но эта статья действительно помогла мне понять, что такое компоненты. Оказывается, это основные элементы числа, на которые его можно разделить. Какие примеры приведены в статье! Теперь я понимаю, что можно разбить число на разряды, единицы, десятки и сотни. Такой подход помогает лучше понять структуру числа. Спасибо автору за простое и понятное объяснение! Надеюсь, что эта информация поможет моему ребенку лучше усваивать математику.