Что такое lim в математике и как решать такие уравнения
Содержимое
- 1 Что такое lim в математике и как решать такие уравнения
- 1.1 Определение lim в математике
- 1.2 Видео по теме:
- 1.3 Что означает лимит в математике и как его записывают
- 1.4 Свойства лимитов и их использование в математических выкладках
- 1.5 Вопрос-ответ:
- 1.5.0.1 Что такое понятие «lim» в математике?
- 1.5.0.2 Как решать уравнения с пределами?
- 1.5.0.3 Какие свойства пределов можно использовать для решения уравнений?
- 1.5.0.4 Как можно упростить уравнение с пределами перед решением?
- 1.5.0.5 Как найти значения аргументов, при которых значение функции или последовательности равно пределу?
- 1.5.0.6 Что такое предел в математике?
- 1.6 Решение уравнений с пределами
- 1.7 Методы решения уравнений с пределами
- 1.8 Примеры решения уравнений с пределами
- 1.9 Сложные уравнения с пределами и способы их решения
- 1.10 Практическое применение уравнений с пределами в математике и физике
Узнайте, что такое lim в математике и как решать уравнения с пределами. Научитесь находить предел функции и понимать его геометрическую интерпретацию.
В математике предел (обозначается как lim) является одним из основных понятий и используется для определения поведения функции или последовательности при приближении к определенной точке или бесконечности. Предел позволяет оценить, как функция ведет себя на бесконечно удаленных от точки значениях.
Решение уравнений с пределами существенно отличается от решения обычных уравнений. Вместо нахождения конкретного значения переменной, в уравнениях с пределами мы ищем поведение функции вблизи определенной точки. Это может быть полезно, например, для определения асимптот функции или нахождения ее экстремумов.
Для решения уравнений с пределами часто используются такие инструменты, как правила Лопиталя, разложение функции в ряд Тейлора или применение известных формул пределов.
Пределы играют важную роль в математическом анализе и других областях, таких как физика и экономика. Они позволяют более точно описывать и понимать поведение функций и последовательностей и используются в широком спектре задач и приложений.
Определение lim в математике

Формально, предел функции f(x) при x, стремящемся к числу a, обозначается следующим образом:
lim(x → a) f(x) = L,
где L — это значение, к которому сходится функция f(x) при x, приближающемся к a.
Для понимания предела необходимо уяснить, что значение функции в точке a может отличаться от предела, так как предел определяется поведением функции при приближении аргумента, а не в самой точке. Предел позволяет рассмотреть функцию в окрестности точки a и определить ее поведение в этой окрестности.
Знание определения предела позволяет решать различные задачи, связанные с нахождением асимптот, точек разрыва, максимальных и минимальных значений функций и т. д. Оно необходимо для изучения дифференциального и интегрального исчисления, а также для более глубокого понимания математических концепций и их применения в реальных задачах.
Видео по теме:
Что означает лимит в математике и как его записывают
Лимиты обычно записываются с использованием символа «lim». Например, «lim x → a f(x)» означает, что значение функции f(x) стремится к определенному числу a при приближении x к некоторому значению.
В записи лимитов также могут использоваться математические символы, такие как «+∞» или «-∞», чтобы обозначить бесконечность. Например, «lim x → +∞ f(x)» означает, что значение функции f(x) стремится к бесконечности при приближении x к положительной бесконечности.
Для решения уравнений с пределами необходимо использовать различные методы, такие как арифметические преобразования, правила дифференцирования и интегрирования, а также теоремы о пределах. Важно учитывать особые случаи, такие как разрывы функции или точки, в которых функция не определена.
Свойства лимитов и их использование в математических выкладках

Вот несколько основных свойств лимитов:
- Сумма лимитов: лимит суммы двух функций равен сумме их лимитов. То есть, если f(x) и g(x) имеют пределы при x, стремящемся к некоторому значению a, то предел суммы f(x) + g(x) при x, стремящемся к a, будет равен сумме пределов этих функций.
- Произведение лимитов: лимит произведения двух функций равен произведению их лимитов. То есть, если f(x) и g(x) имеют пределы при x, стремящемся к a, то предел произведения f(x) * g(x) при x, стремящемся к a, будет равен произведению пределов этих функций.
- Частное лимитов: лимит частного двух функций равен частному их лимитов. То есть, если f(x) и g(x) имеют пределы при x, стремящемся к a, и g(x) не равно нулю, то предел частного f(x) / g(x) при x, стремящемся к a, будет равен частному пределов этих функций.
- Лимит композиции функций: если функция f(x) имеет предел при x, стремящемся к a, и функция g(x) имеет предел при x, стремящемся к b, то предел композиции f(g(x)) при x, стремящемся к a, будет равен пределу f(x) при x, стремящемся к b.
Используя эти свойства, можно упростить выражения и решить уравнения с пределами, делая математические выкладки более эффективными и удобными.
Вопрос-ответ:
Что такое понятие «lim» в математике?
В математике «lim» является сокращением от слова «лимит» и обозначает предел функции или последовательности. Предел функции определяется как значение, к которому стремится функция при приближении аргумента к определенному значению или бесконечности. Предел последовательности определяется как значение, к которому стремятся ее члены при увеличении номера члена последовательности.
Как решать уравнения с пределами?
Для решения уравнений с пределами необходимо использовать определение предела функции или последовательности, а также знания о свойствах пределов. Сначала необходимо упростить уравнение, а затем найти предельное значение функции или последовательности на обеих сторонах уравнения. Затем используя свойства пределов, можно найти значения аргументов, при которых значение функции или последовательности равно пределу.
Какие свойства пределов можно использовать для решения уравнений?
Для решения уравнений с пределами можно использовать такие свойства пределов, как арифметические свойства (сложение, вычитание, умножение, деление), свойства предела суммы, разности, произведения и отношения двух функций или последовательностей, а также свойство предела композиции функций.
Как можно упростить уравнение с пределами перед решением?
Для упрощения уравнения с пределами перед решением можно использовать арифметические свойства пределов, такие как свойство суммы, разности, произведения и отношения. Также можно применить свойство предела композиции функций, если уравнение содержит сложную функцию.
Как найти значения аргументов, при которых значение функции или последовательности равно пределу?
Чтобы найти значения аргументов, при которых значение функции или последовательности равно пределу, необходимо сравнить выражение функции или последовательности с пределом и решить получившееся уравнение. Для этого можно использовать алгебраические методы решения уравнений, такие как факторизация, квадратное уравнение, системы уравнений и т.д.
Что такое предел в математике?
Предел в математике — это значение, к которому стремится функция при приближении аргумента к определенному значению или при его бесконечном увеличении. Он позволяет определить поведение функции в окрестности данной точки или на бесконечности.
Решение уравнений с пределами
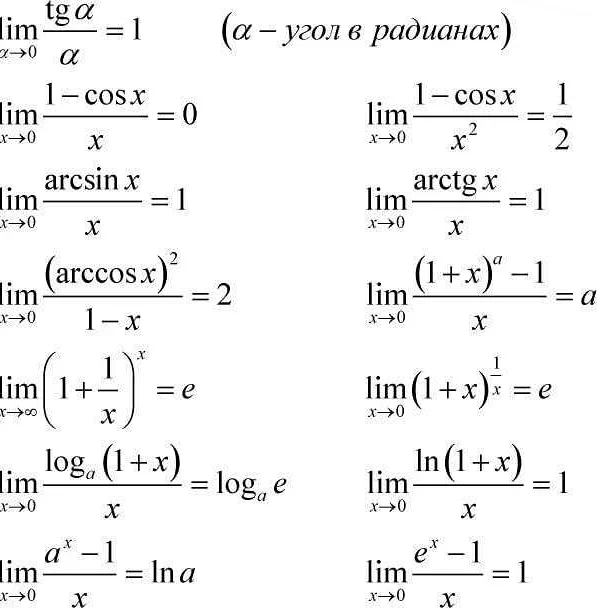
Для решения уравнений с пределами необходимо учитывать основные свойства пределов. Например, если имеется уравнение вида:
lim (f(x) + g(x)) = L,
где f(x) и g(x) — функции, а L — конечный предел, то для решения такого уравнения необходимо рассмотреть пределы каждой функции f(x) и g(x) по отдельности и применить правила арифметики пределов.
Если в уравнении присутствуют сложные функции, то необходимо использовать более сложные методы решения, например, методы Лопиталя или разложение в ряд Тейлора.
Важно помнить, что решение уравнений с пределами может быть не всегда однозначным, и в некоторых случаях может потребоваться применение специальных методов или приближенных вычислений.
Таким образом, знание основных свойств пределов и умение применять их при решении уравнений с пределами является важным навыком для успешного изучения математического анализа.
Методы решения уравнений с пределами
Уравнения с пределами, также называемые предельными уравнениями, представляют собой математические уравнения, в которых встречаются пределы. Решение таких уравнений требует применения специальных методов и приемов.
Один из методов решения уравнений с пределами — это использование арифметических свойств пределов. С помощью этих свойств можно переставлять операции и выражения, упрощать выражения и приводить уравнение к более простому виду.
Еще одним методом решения уравнений с пределами является замена переменной. Иногда замена переменной позволяет упростить уравнение или привести его к более удобному виду для дальнейшего анализа.
Другим методом решения уравнений с пределами является применение теоремы о двух милиционерах. Эта теорема позволяет находить пределы сложных функций путем разложения их на более простые составляющие.
Также для решения уравнений с пределами можно использовать графический метод. С помощью построения графика функции можно наглядно представить ее поведение и определить значения пределов.
Все эти методы имеют свои особенности и применяются в зависимости от сложности уравнения и доступных инструментов. Важно уметь выбирать подходящий метод решения и грамотно применять его для получения корректных результатов.
МетодОписание
| Арифметические свойства пределов | Позволяют переставлять операции и выражения, упрощать выражения и приводить уравнение к более простому виду |
| Замена переменной | Позволяет упростить уравнение или привести его к более удобному виду для дальнейшего анализа |
| Теорема о двух милиционерах | Позволяет находить пределы сложных функций путем разложения их на более простые составляющие |
| Графический метод | Позволяет наглядно представить поведение функции и определить значения пределов |
Примеры решения уравнений с пределами

Пример 1:
Рассмотрим уравнение с пределами:
lim x → 2 (x^2 — 4) = 0
Для решения данного уравнения с пределами, мы можем использовать прямое подстановочное значение, так как функция в данном случае является непрерывной.
Подставим значение x = 2 в уравнение:
(2)^2 — 4 = 0
4 — 4 = 0
0 = 0
Таким образом, уравнение с пределами lim x → 2 (x^2 — 4) = 0 имеет решение x = 2.
Пример 2:
Рассмотрим уравнение с пределами:
lim x → 0 (3x + 1) = k
Для решения данного уравнения с пределами, мы должны найти значение k, при котором предел существует.
Подставим значение x = 0 в уравнение:
3(0) + 1 = k
0 + 1 = k
k = 1
Таким образом, уравнение с пределами lim x → 0 (3x + 1) = k имеет решение k = 1.
Пример 3:
Рассмотрим уравнение с пределами:
lim x → ∞ (2x + 3) = ∞
Для решения данного уравнения с пределами, мы должны показать, что предел функции стремится к бесконечности.
Рассмотрим произвольное положительное число M. Найдем значение N, такое что:
2x + 3 > M, когда x > N
Решим это неравенство:
2x + 3 > M
2x > M — 3
x > (M — 3)/2
Выберем N так, чтобы N > (M — 3)/2. Таким образом, при x > N, предел функции будет больше M.
Таким образом, уравнение с пределами lim x → ∞ (2x + 3) = ∞ имеет решение x > N, где N — некоторое положительное число.
Сложные уравнения с пределами и способы их решения
При решении уравнений с пределами, которые содержат сложные функции или комбинации нескольких функций, необходимо использовать определенные методы и приемы.
Один из таких методов — это применение правила Лопиталя. Оно позволяет упростить сложные уравнения, когда пределы функций в числителе и знаменателе стремятся к нулю или бесконечности. Правило Лопиталя используется для нахождения предела отношения производных функций.
Еще один способ решения сложных уравнений с пределами — это применение разложения в ряд Тейлора. Этот метод позволяет приближенно вычислить значение функции в окрестности заданной точки. Разложение в ряд Тейлора основано на разложении функции в бесконечную сумму степеней переменной.
Также стоит учитывать, что при решении уравнений с пределами может потребоваться использование свойств пределов функций, таких как предел суммы, разности, произведения или частного функций.
При решении сложных уравнений с пределами необходимо быть внимательным и аккуратным, учитывая все особенности и свойства функций, чтобы получить правильный результат.
Практическое применение уравнений с пределами в математике и физике
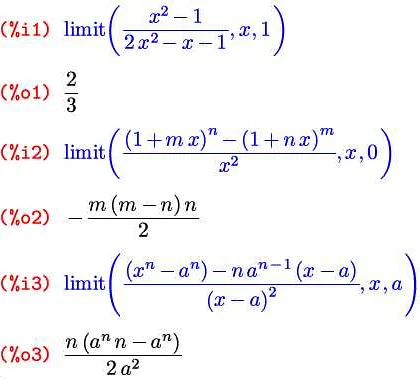
Уравнения с пределами широко применяются в математике и физике для решения различных задач. Они позволяют описать поведение функций в окрестности определенной точки и выявить особенности их графиков.
В математике уравнения с пределами используются для нахождения значений функций в точках, когда аргумент стремится к определенному значению. Например, предел функции может быть использован для определения горизонтальной асимптоты, вертикальной асимптоты или точки разрыва. Также пределы используются для нахождения производных и интегралов функций.
В физике уравнения с пределами играют важную роль при моделировании физических процессов. Например, пределы могут быть использованы для определения скорости изменения физической величины, момента инерции или силы. Они помогают описать поведение системы в пределе бесконечно малого изменения.
Конкретные примеры применения уравнений с пределами в математике и физике включают нахождение скорости свободного падения, расчет траектории движения тела под действием силы тяжести, определение максимального и минимального значения функции на заданном интервале, анализ гармонических колебаний и многое другое.
Важно отметить, что для решения уравнений с пределами требуется использовать математические методы, такие как правила Лопиталя, свойства пределов и дифференцирования, интегрирование и т.д. Также необходимо учитывать физические законы и условия задачи для получения корректного решения.
Использование уравнений с пределами позволяет более точно описывать и предсказывать различные явления и процессы в математике и физике, что делает их неотъемлемой частью этих наук.

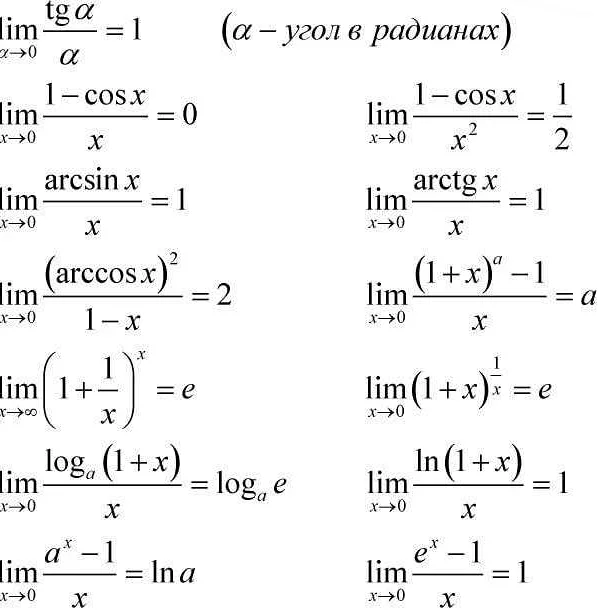



Очень интересная статья! Никогда не думал, что понятие предела в математике может быть настолько важным и полезным. Честно говоря, всегда было сложно понимать, как решать уравнения с пределами, но теперь все стало намного яснее. Особенно порадовало, что в статье есть пошаговые инструкции и примеры, которые помогают лучше усвоить материал. Теперь я буду гораздо увереннее работать с уравнениями, содержащими пределы. Большое спасибо за такую полезную информацию! Жду с нетерпением новых статей на эту тему.