Что такое в математике lim

Что такое предел в математике и как его вычислить. Понятие предела и его свойства. Примеры вычисления пределов функций.

lim – это сокращение от латинского слова «limitis», что означает «граница» или «предел». В математике, предел функции представляет собой значение, к которому стремится функция при приближении ее аргумента к определенному значению или приближении его к бесконечности. Пределы широко используются в различных областях математики, включая анализ, дифференциальное исчисление, интегральное исчисление и теорию вероятностей.

Для обозначения предела функции используется символ «lim». Например, если функция f(x) стремится к значению L при приближении аргумента x к значению a, записывается как:

limx→a f(x) = L

В этой формуле «lim» обозначает предел, «x→a» указывает на приближение аргумента x к значению a, «f(x)» — функция, а «L» — искомое значение предела.

Концепция предела позволяет анализировать и понимать поведение функций в окрестности определенных точек. Она также позволяет решать различные задачи, такие как определение непрерывности функции, нахождение производных и интегралов, и изучение поведения функций на бесконечности.

Определение и примеры математического лимита

Чтобы формально определить лимит функции, используется символичное обозначение «lim». Например, «lim(x->a) f(x) = L» означает, что функция f(x) имеет предельное значение L при приближении аргумента x к значению a.

Примером может служить функция f(x) = 1/x. Если мы рассмотрим лимит этой функции при x стремящемся к бесконечности (lim(x->∞) f(x)), то можно заметить, что при увеличении значения x, значение функции f(x) стремится к нулю. То есть, lim(x->∞) f(x) = 0.

Еще один пример — функция g(x) = sin(x)/x. Здесь, если мы рассмотрим лимит этой функции при x стремящемся к нулю (lim(x->0) g(x)), то значение функции g(x) будет равно 1. То есть, lim(x->0) g(x) = 1.

ФункцияЛимит

f(x) = 1/x	lim(x->∞) f(x) = 0
g(x) = sin(x)/x	lim(x->0) g(x) = 1

Что такое математический лимит?

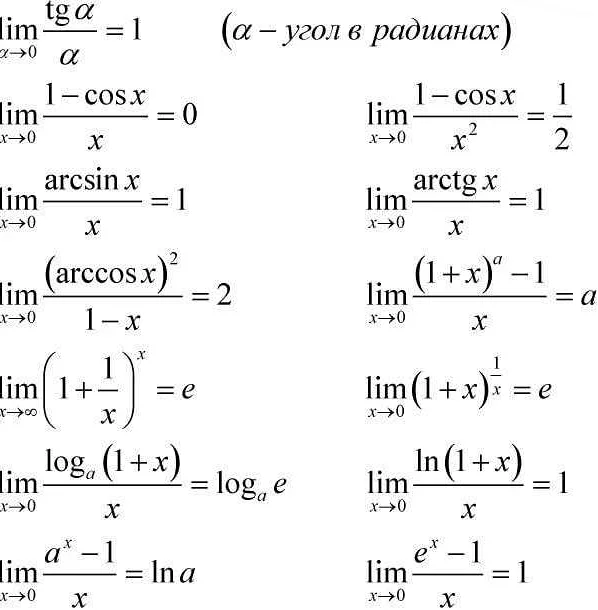
Формально, лимит функции f(x) при x, стремящемся к a, обозначается следующим образом:

lim

f(x)

= L

,

если

для каждого

ε > 0

существует

δ > 0

такое, что

|f(x) — L| < ε

для каждого

x

такого, что

0 < |x — a| < δ

Здесь f(x) — функция, a — точка, L — предельное значение, ε — положительное число (произвольно малая величина), а δ — положительное число (окрестность точки a).

Основная идея лимита заключается в том, что значение функции f(x) стремится к предельному значению L, когда x приближается к a. Это означает, что можно выбрать сколь угодно малое положительное число ε, и существует такое положительное число δ, что если значение x находится в окрестности точки a, отличной от нуля, то |f(x) — L| будет меньше, чем ε.

Лимиты широко используются в математике для определения непрерывности функций, нахождения производных, решения уравнений и многих других задач. Они позволяют анализировать поведение функций вблизи определенной точки и делать выводы о их свойствах.

Определение лимита в математике

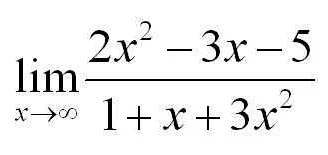
lim(x→a) f(x) = L

где a – точка, к которой стремится переменная x, f(x) – функция, а L – предел функции f(x) при x, стремящемся к a.

Формальное определение лимита в математике говорит, что для любого достаточно малого положительного числа ε, существует такое положительное число δ, что для всех точек x, удовлетворяющих условию 0 < |x — a| < δ, выполняется неравенство |f(x) — L| < ε.

По сути, лимит функции f(x) при x, стремящемся к a, показывает, к какому значению приближается функция, когда ее аргумент приближается к определенной точке. Если лимит существует и равен L, то говорят, что функция f(x) имеет предел L при x, стремящемся к a.

Примеры вычисления лимитов

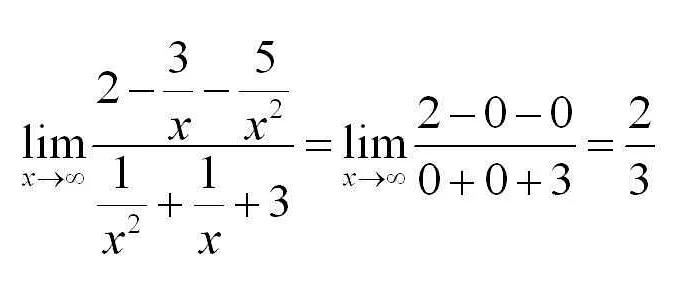
Рассмотрим несколько примеров вычисления лимитов:

ПримерЛимит

lim(x → 2) (3x + 5)	11
lim(x → ∞) (1/x)	0
lim(x → 0) (sin(x)/x)	1
lim(x → 0) (1/x)	не существует

В первом примере, при приближении x к 2, функция 3x + 5 стремится к 11.

Во втором примере, при x, стремящемся к бесконечности, функция 1/x стремится к 0.

Третий пример демонстрирует, что при x, стремящемся к 0, отношение sin(x)/x стремится к 1.

В последнем примере, при x, стремящемся к 0, функция 1/x не имеет предела, поскольку она становится бесконечно большой.

Как вычислить лимит функции?

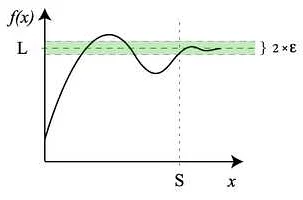
Для вычисления лимита функции необходимо использовать определение предела и различные методы его вычисления. Предел функции определяется как значение, к которому стремится функция при приближении аргумента к определенной точке.

Существует несколько основных методов вычисления лимитов функций. Один из них — метод подстановки. В этом методе необходимо подставить значение, к которому стремится аргумент, вместо самого аргумента в выражение функции и вычислить полученное выражение. Если результат существует и конечен, то это и будет значение лимита функции.

Еще один метод — метод арифметических операций. В этом методе необходимо разложить функцию на простые элементарные функции и использовать известные пределы этих функций для получения значения лимита. Например, если функция представлена в виде суммы или произведения функций, то можно использовать свойства сложения или умножения пределов соответственно.

Один из самых часто используемых методов — метод замены переменной. В этом методе необходимо заменить аргумент функции на новую переменную, которая стремится к той же точке, и выразить функцию через эту новую переменную. Затем можно использовать известные пределы функции от новой переменной для вычисления лимита.

Также существуют методы Лопиталя и де Л’Опиталя, которые позволяют вычислить некоторые неопределенности вида 0/0 или ∞/∞. Они основываются на использовании производных функций и правиле Лопиталя.

Вычисление лимита функции может быть сложным и требует хорошего понимания математических операций и свойств функций. Поэтому при вычислении лимитов рекомендуется использовать все доступные методы и свойства функции для получения наиболее точного результата.

Предел функции и его свойства

Основное свойство предела функции заключается в том, что он определен единственным образом. Если предел функции существует, то он будет иметь только одно значение. Если же предел не существует, то говорят, что функция расходится.

Предел функции обладает несколькими важными свойствами:

1. Аддитивное свойство: предел суммы двух функций равен сумме их пределов.
2. Мультипликативное свойство: предел произведения двух функций равен произведению их пределов.
3. Свойство сжатой функции: если функция ограничена сверху и снизу другой функцией, предел этих функций будет равен.
4. Свойство монотонности: если функция возрастает или убывает в окрестности точки, ее предел будет равен максимальному или минимальному значению в этой окрестности соответственно.

Знание свойств предела функции позволяет более удобно и эффективно работать с функциями в математическом анализе и других областях, где используется математика.

Применение лимитов в математике и физике

В математике лимиты используются для определения пределов функций. Например, при решении уравнений или нахождении точек максимума или минимума функций, знание лимитов играет важную роль. Они позволяют нам определить, как функция ведет себя вблизи определенной точки или как она стремится к определенному значению при приближении к бесконечности.

В физике лимиты используются для описания изменения переменных в течение времени. Например, при моделировании движения тела или изменения температуры в пространстве, знание лимитов позволяет нам анализировать, как эти переменные меняются со временем и при каких условиях они достигают предельных значений.

Понимание лимитов также позволяет нам проводить анализ исключительных ситуаций. Например, при решении задач о скорости или ускорении движения тела, знание лимитов позволяет нам определить, какие значения скорости или ускорения невозможны или являются исключительными.

Таким образом, применение лимитов в математике и физике позволяет нам более точно и подробно анализировать и описывать различные явления и процессы. Они позволяют нам понять, как функции и переменные ведут себя в различных условиях и приближениях, и как они связаны друг с другом.

Что такое бесконечный предел?

Функция имеет бесконечный предел приближения, если значения функции становятся все больше и больше по мере приближения к определенной точке или значению переменной. Например, если функция f(x) стремится к бесконечности при x, стремящемся к бесконечности, то это можно записать как

lim f(x) = ∞, при x → ∞

Такой вид предела говорит о том, что значения функции f(x) становятся все больше и больше по мере увеличения значения x и неограниченно стремятся к бесконечности.

Бесконечный предел может быть положительным (∞), отрицательным (-∞) или неопределенным (если приближение к бесконечности осуществляется с двух сторон и значения функции не имеют определенного знака).

Примером функции с бесконечным пределом может быть функция y = 1/x, где x стремится к 0. В этом случае, приближаясь к нулю, значения функции y становятся все больше и больше, а значит, имеется бесконечный предел y → ∞ при x → 0.

Бесконечный предел является важным понятием в математике и используется для анализа поведения функций в пределах определенных значений или точек. Знание бесконечного предела позволяет определить, как функция ведет себя в окрестности определенной точки или значения переменной и делать выводы о ее характеристиках и свойствах.

Видео по теме:

Что означает понятие «лимит» в математике?

В математике «лимит» — это значение, к которому стремится функция или последовательность при приближении аргумента к определенной точке или бесконечности.

Как определить, что функция имеет предел?

Функция имеет предел, если существует такое число, что значение функции приближается к этому числу при достаточно близких значениях аргумента.

Как записывается понятие предела функции в математике?

Понятие предела функции записывается как «lim f(x) = L», где «f(x)» — функция, «L» — предел функции при приближении аргумента «x» к определенной точке или бесконечности.

Какие существуют типы пределов функций?

Существуют три основных типа пределов функций: предел функции при приближении аргумента к точке, предел функции при приближении аргумента к плюс бесконечности и предел функции при приближении аргумента к минус бесконечности.

Что такое предел в математике?

Предел в математике — это значение, к которому стремится функция или последовательность при приближении аргумента к определенной точке. Он позволяет определить поведение функции вблизи этой точки и дает информацию о ее свойствах и особенностях.

Как определить предел функции?

Для определения предела функции необходимо проанализировать ее поведение при приближении аргумента к определенной точке. Для этого используются различные методы, такие как арифметические операции с пределами, теоремы о пределе композиции функций, правило Лопиталя и другие. Кроме того, предел функции можно вычислить с помощью графического анализа или численных методов, таких как метод Ньютона.