Что такое математические операции

Математические операции – это действия, выполняемые над числами, которые позволяют получить новые числа или изменить уже имеющиеся. Операции включают сложение, вычитание, умножение и деление, а также возведение в степень и извлечение корня. Понимание и умение правильно использовать математические операции являются основой для решения различных задач и проблем в математике и ее приложениях.

Математические операции — это основные действия, которые выполняются с числами для получения новых результатов. Они позволяют решать различные задачи и рассчитывать значения в разных областях науки, техники и экономики.

В математике существует несколько основных операций: сложение, вычитание, умножение и деление. Каждая из них имеет свои правила и свойства, которые позволяют выполнять вычисления точно и последовательно.

Сложение — это операция, которая позволяет объединять два или более числа в одно. Например, если у нас есть два числа: 3 и 5, то сложение этих чисел даст нам результат 8.

Вычитание — это операция, которая позволяет находить разницу между двумя числами. Например, если у нас есть два числа: 7 и 4, то вычитание этих чисел даст нам результат 3.

Умножение — это операция, которая позволяет находить произведение двух чисел. Например, если у нас есть два числа: 2 и 6, то умножение этих чисел даст нам результат 12.

Деление — это операция, которая позволяет находить частное от деления одного числа на другое. Например, если у нас есть два числа: 10 и 2, то деление этих чисел даст нам результат 5.

Математические операции являются неотъемлемой частью математики и играют важную роль в решении различных задач. Понимание основных понятий и примеров математических операций поможет вам лучше разобраться в этой области знаний и применять их в практических ситуациях.

Основные понятия математических операций

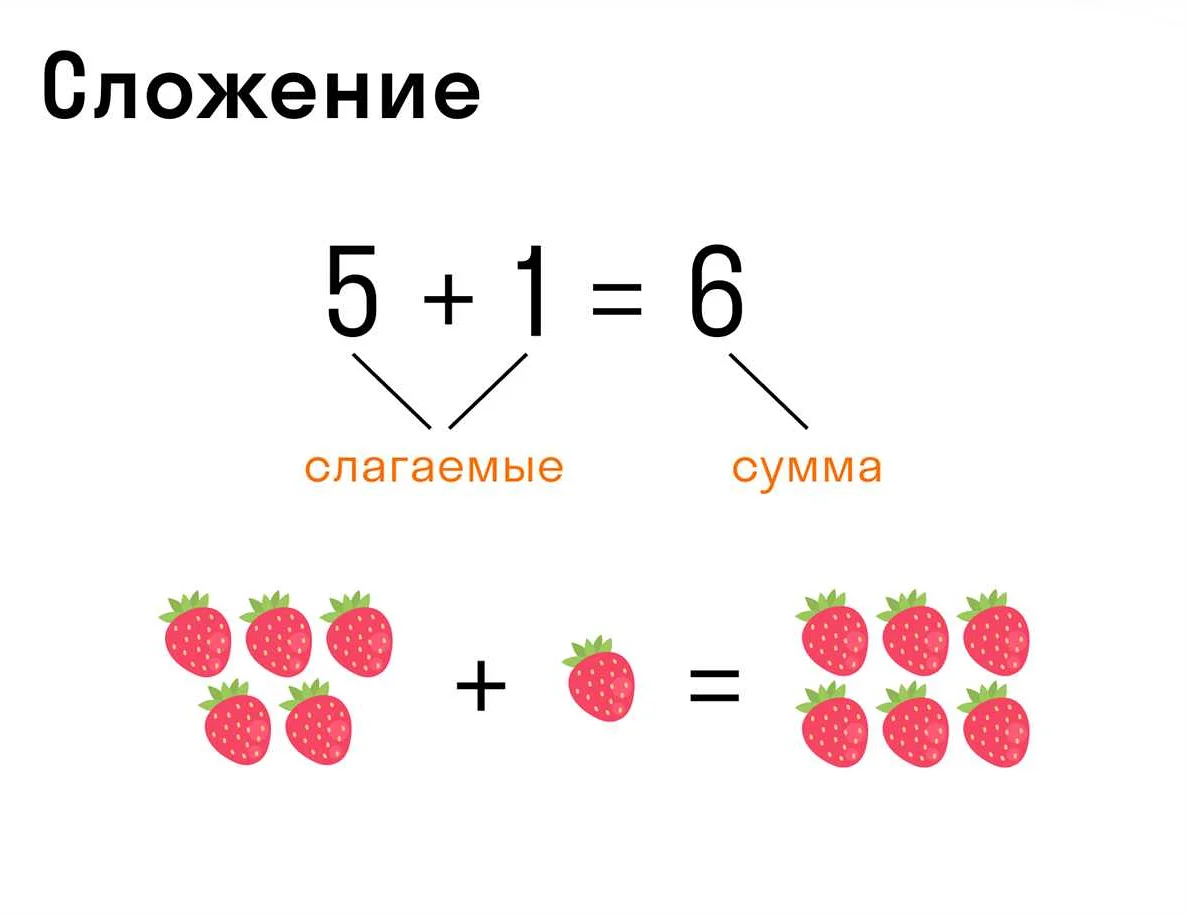
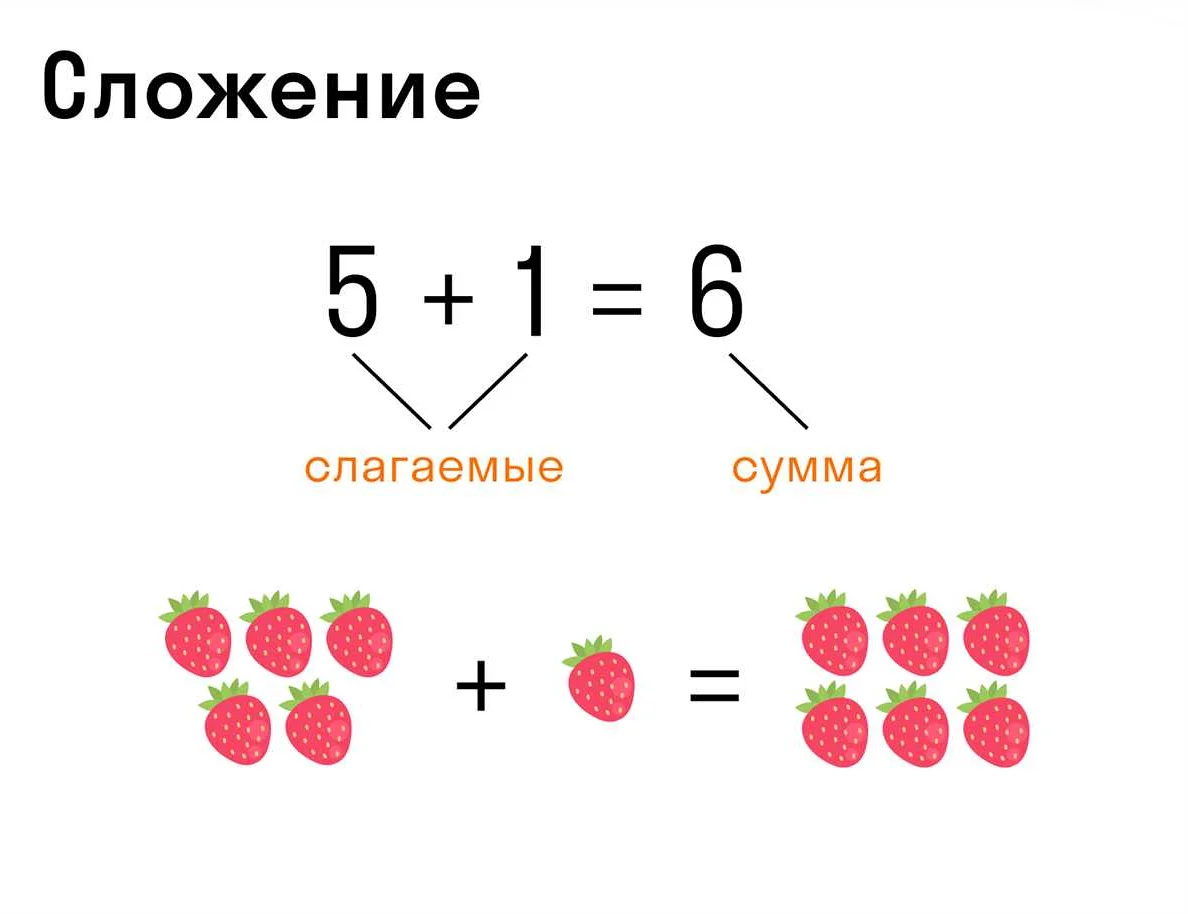
Сложение – это операция, при которой два или более числа суммируются для получения общей суммы. Например, сумма чисел 3 и 5 равна 8: 3 + 5 = 8. Сложение можно представить геометрически в виде объединения отрезков на числовой прямой.

Вычитание – это операция, при которой из одного числа вычитается другое число для получения разности. Например, разность чисел 8 и 3 равна 5: 8 — 3 = 5. Вычитание можно представить геометрически в виде отрезания отрезка на числовой прямой.

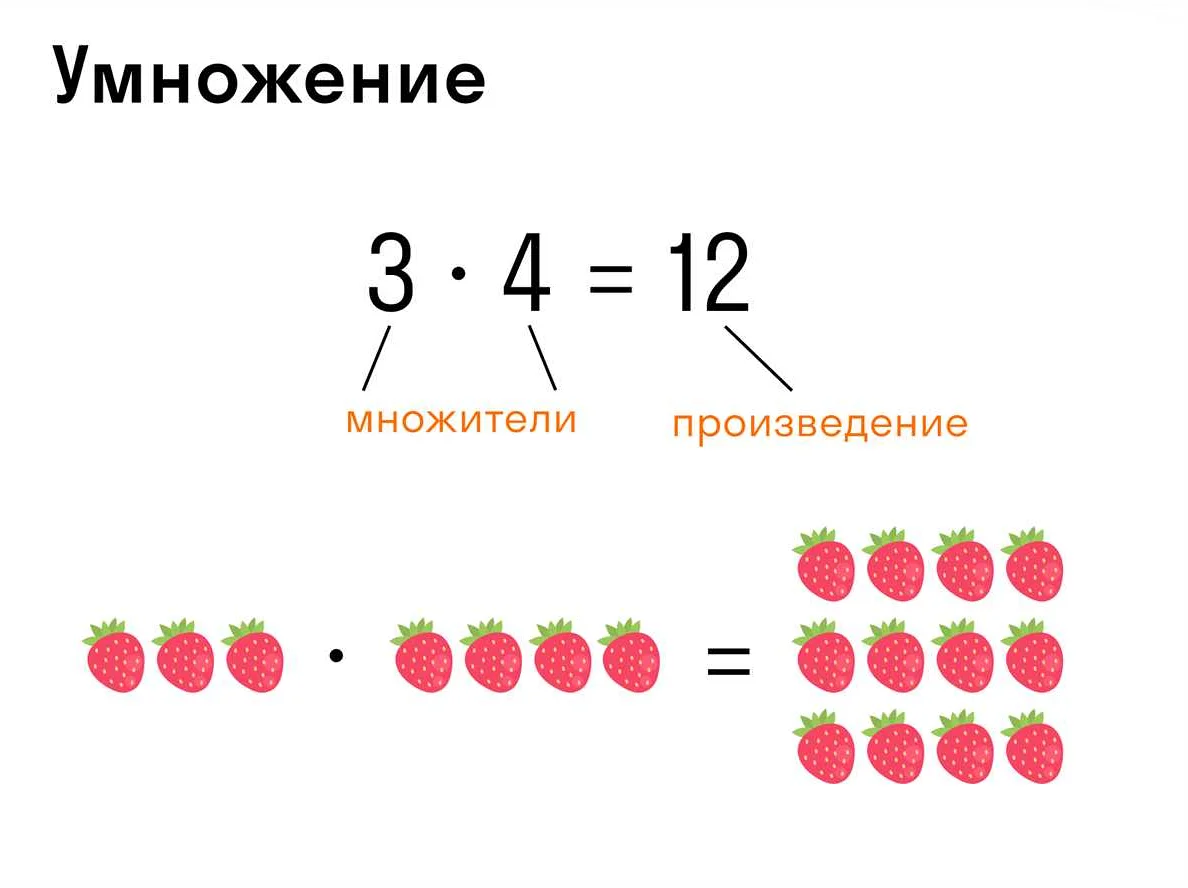
Умножение – это операция, при которой одно число увеличивается в несколько раз или умножается на другое число. Например, произведение чисел 4 и 6 равно 24: 4 * 6 = 24. Умножение можно представить геометрически в виде повторения отрезка на числовой прямой.

Деление – это операция, при которой одно число делится на другое число для получения частного. Например, частное от деления числа 15 на число 3 равно 5: 15 / 3 = 5. Деление можно представить геометрически в виде разделения отрезка на числовой прямой.

Все математические операции имеют свои правила и свойства, которые позволяют выполнять сложные вычисления. Знание и понимание этих операций является важным основанием для изучения математики и ее применения в различных областях науки и жизни.

Арифметические операции: сложение, вычитание, умножение, деление

Сложение — это операция, при которой два или более числа объединяются в одно число, которое называется суммой. Для сложения используется знак «+».

Примеры сложенияРезультат

3 + 5	8
10 + (-2)	8

Вычитание — это операция, при которой одно число вычитается из другого числа, получая разность. Для вычитания используется знак «-«.

Примеры вычитанияРезультат

7 — 4	3
10 — (-2)	12

Умножение — это операция, при которой одно число умножается на другое число, получая произведение. Для умножения используется знак «×» или «*».

Примеры умноженияРезультат

4 × 5	20
(-3) × (-2)	6

Деление — это операция, при которой одно число делится на другое число, получая частное. Для деления используется знак «÷» или «/».

Примеры деленияРезультат

10 ÷ 2	5
16 ÷ (-4)	-4

Операции сравнения: равенство, неравенство, больше, меньше

Одной из основных операций сравнения является операция равенства. Она обозначается символом «=», и позволяет определить, равны ли два числа или значения. Например, выражение «5 = 5» будет истинным, так как оба числа равны.

Операция неравенства обозначается символом «≠» и позволяет определить, не равны ли два числа или значения. Например, выражение «5 ≠ 7» будет истинным, так как числа не равны.

Операция больше (>) позволяет определить, является ли одно число больше другого. Например, выражение «7 > 5» будет истинным, так как число 7 больше числа 5.

Операция меньше (

ОперацияОбозначениеПримерРезультат

Равенство	=	5 = 5	Истина
Неравенство	≠	5 ≠ 7	Истина
Больше	>	7 > 5	Истина
Меньше	<	5 < 7	Истина

Операции сравнения широко используются в математике, программировании и других областях, где необходимо сравнивать числа и значения.

Операции со множествами: объединение, пересечение, разность

Объединение множеств — это операция, при которой создается новое множество, содержащее все элементы, присутствующие хотя бы в одном из исходных множеств. Обозначается символом «∪». Например, если даны два множества A = {1, 2, 3} и B = {3, 4, 5}, то их объединение A ∪ B будет равно {1, 2, 3, 4, 5}.

Пересечение множеств — это операция, при которой создается новое множество, содержащее только элементы, присутствующие в обоих исходных множествах. Обозначается символом «∩». Например, если даны два множества A = {1, 2, 3} и B = {3, 4, 5}, то их пересечение A ∩ B будет равно {3}.

Разность множеств — это операция, при которой создается новое множество, содержащее только элементы, присутствующие в первом исходном множестве, но отсутствующие во втором исходном множестве. Обозначается символом «\» или «-«. Например, если даны два множества A = {1, 2, 3} и B = {3, 4, 5}, то их разность A \ B будет равно {1, 2}.

ОперацияОбозначениеПример

Объединение	∪	A ∪ B = {1, 2, 3, 4, 5}
Пересечение	∩	A ∩ B = {3}
Разность	\ или —	A \ B = {1, 2}

Операции с числами: возведение в степень, извлечение корня

Возведение числа в степень означает, что число умножается само на себя определенное количество раз. Например, возведение числа 2 в степень 3 обозначается как 2^3 и равно 2*2*2 = 8. Здесь число 2 называется основанием, а число 3 – показателем степени.

Если показатель степени положителен, то происходит умножение числа на себя нужное количество раз. Если показатель степени равен нулю, то результатом будет 1. Если показатель степени отрицателен, то сначала выполняется обратная операция – извлечение корня, а затем полученное значение возводится в степень с положительным показателем.

Извлечение корня – это обратная операция к возведению в степень. Если число a является n-й степенью числа b, то a называется корнем степени n из числа b: a = √b. Например, корень квадратный из числа 9 равен 3, так как 3^2 = 9.

Различные операции с числами, такие как возведение в степень и извлечение корня, широко применяются в математике, физике, программировании и других областях науки и техники. Понимание этих операций позволяет решать сложные задачи и проводить различные вычисления.

Логические операции: конъюнкция, дизъюнкция, отрицание

Конъюнкция, также известная как логическое «И», обозначается символом «&» или «∧». Она возвращает истинное значение только тогда, когда оба операнда являются истинными. Если один или оба операнда являются ложными, то результат будет ложным. Например, выражение (5 > 3) ∧ (2 + 2 = 4) будет истинным, так как оба операнда истинны.

Дизъюнкция, тоже известная как логическое «ИЛИ», обозначается символом «||» или «∨». Она возвращает истинное значение, если хотя бы один из операндов является истинным. Если оба операнда ложны, то результат будет ложным. Например, выражение (5 > 3) ∨ (2 + 2 = 5) будет истинным, так как один из операндов истинный.

Отрицание, обозначаемое символом «¬» или «!». Оно меняет логическое значение операнда на противоположное. Если операнд истинный, то результат будет ложным, и наоборот. Например, выражение ¬(5 > 3) будет ложным, так как операнд истинный.

Логические операции могут быть использованы в различных сферах, таких как программирование, математика, философия и т.д. Они позволяют нам делать сложные логические вычисления и принимать решения на основе этих вычислений.

Важно помнить, что результаты логических операций всегда являются логическими значениями и могут быть использованы в дальнейших вычислениях или условных операторах.

Операции с дробями: сложение, вычитание, умножение, деление

Сложение дробей производится путем сложения числителей и знаменателей дробей. Если знаменатели дробей одинаковы, то сложение производится просто путем сложения числителей. Если знаменатели различны, требуется привести дроби к общему знаменателю.

Вычитание дробей производится путем вычитания числителей и знаменателей дробей. Как и в случае со сложением, знаменатели дробей должны быть одинаковыми.

Умножение дробей осуществляется путем умножения числителей и знаменателей дробей. Результатом умножения двух дробей будет новая дробь, у которой числитель равен произведению числителей, а знаменатель — произведению знаменателей.

Деление дробей производится путем умножения делимой дроби на обратную дробь. Для того чтобы найти обратную дробь, необходимо поменять местами числитель и знаменатель. Затем выполняется умножение полученной дроби на делимую дробь.

Знание операций с дробями является необходимым для работы с рациональными числами и решения математических задач.

Примеры математических операций в реальной жизни

• При покупке товаров в магазине нам необходимо произвести операцию сложения, чтобы посчитать общую стоимость покупок. Например, если мы купили яблоки за 50 рублей, апельсины за 70 рублей и бананы за 30 рублей, то сумма нашей покупки будет равна 50 + 70 + 30 = 150 рублей.
• При расчете времени мы также используем математические операции. Если, например, мы хотим узнать, сколько времени займет нам добраться из одного города в другой, мы можем использовать операцию вычитания. Зная, что путь займет 4 часа, а мы выезжаем в 9 утра, мы можем вычислить, что мы прибудем в город назначения в 9 + 4 = 13 часов.
• В области финансовых инвестиций, мы также можем применять математические операции. Например, если у нас есть сумма вклада, которая составляет 1000 долларов, и мы хотим рассчитать конечную сумму с учетом процентной ставки 5% в год, мы можем использовать операцию умножения. Итоговая сумма будет равна 1000 * (1 + 0.05) = 1050 долларов.

Это всего лишь несколько примеров использования математических операций в реальной жизни. Они помогают нам решать различные задачи, позволяют нам понять и применять математические концепции в повседневных ситуациях.

Вопрос-ответ:

Зачем нужны математические операции?

Математические операции нужны для выполнения различных вычислений и решения математических задач. Они позволяют складывать, вычитать, умножать и делить числа, а также выполнять другие действия с числами.

Какие основные математические операции существуют?

Основные математические операции включают сложение, вычитание, умножение и деление. Кроме того, существуют такие операции как возведение в степень, извлечение корня, нахождение остатка от деления и другие.

Как правильно выполнять математические операции?

Для выполнения математических операций необходимо знать правила и порядок их выполнения. Обычно сначала выполняются операции в скобках, затем умножение и деление, и в конце сложение и вычитание. Для более сложных операций существуют специальные алгоритмы и методы решения.

Можно ли комбинировать разные математические операции в одном выражении?

Да, в математике можно комбинировать различные операции в одном выражении. Например, можно сложить или вычесть числа, умножить или разделить результаты операций, а также использовать скобки для указания порядка выполнения операций.

Какие примеры математических операций можно привести?

Примеры математических операций включают сложение двух чисел, например, 2 + 3 = 5, вычитание одного числа из другого, например, 5 — 2 = 3, умножение двух чисел, например, 2 * 3 = 6, и деление одного числа на другое, например, 6 / 2 = 3. Также можно привести примеры более сложных операций, например, возведение числа в степень или извлечение корня.

Видео по теме: