Математика как найти корень

Узнайте, как найти корень числа в математике и какие методы используются для нахождения корней. Познакомьтесь с формулами и алгоритмами, которые помогут вам решить задачи, связанные с поиском корней.

Корень числа — это число, которое возведенное в определенную степень дает исходное число. Понимание и умение находить корень числа является важным навыком в математике, который применяется во множестве различных задач и областей, включая физику, инженерию, экономику и статистику.

Существует несколько способов нахождения корня числа, но наиболее распространенным и простым способом является использование операции извлечения корня. Операция извлечения корня является обратной операцией возведения в степень.

Например, корень второй степени числа 9 равен 3, так как 3 умноженное на себя дает 9. То есть, √9 = 3.

В общем случае, чтобы найти корень числа, необходимо использовать специальный математический символ — символ корня. Символ корня выглядит как горизонтальная черта, под которой записывается число, и над которой записывается степень корня.

В данной статье мы рассмотрим различные способы нахождения корня числа, а также предоставим примеры и задачи для практики. Узнайте, как легко и быстро находить корень числа, и применяйте этот навык в своей повседневной жизни и в учебе!

Математика: поиск корня числа — детальное объяснение и примеры

Для поиска корня числа необходимо знать два основных понятия: степень и основание. Степень — это число, указывающее, сколько раз нужно умножить основание на себя. Основание — это число, из которого извлекается корень.

Существуют разные типы корней: квадратный корень (√), кубический корень (∛), четвертный корень (∜) и т. д. В данной статье мы рассмотрим квадратный корень.

Поиск квадратного корня числа выполняется с помощью символа √ или записи в виде числа, возводимого в степень 1/2. Например, квадратный корень из числа 25 обозначается как √25 или 251/2.

Чтобы найти квадратный корень числа, нужно выполнить следующие шаги:

1. Записываем число, из которого нужно извлечь корень.
2. Разбиваем число на простые множители.
3. Группируем множители в пары.
4. Извлекаем корень из каждой пары множителей.
5. Умножаем корни пар множителей и получаем ответ.

Например, чтобы найти квадратный корень числа 36, мы разбиваем его на простые множители: 2 * 2 * 3 * 3. Затем группируем множители в пары: (2 * 2) и (3 * 3). Извлекаем корень из каждой пары множителей: 2 и 3. Далее, умножаем полученные корни пар множителей: 2 * 3 = 6. Таким образом, квадратный корень числа 36 равен 6.

Важно помнить, что квадратный корень может быть как положительным, так и отрицательным числом. Например, квадратный корень из числа 25 будет равен ±5.

Поиск корня числа может быть полезным при решении различных математических задач и позволяет находить значения переменных, выраженные в виде корней.

Теперь вы знаете, как найти корень числа и можете применять этот метод на практике для решения различных задач и уравнений.

Видео по теме:

Основные понятия

Корень n-ной степени числа a обозначается символом √a или a^(1/n), где a — исходное число, n — степень корня.

Квадратный корень числа a равен числу b, при котором b^2 = a. Квадратный корень обозначается символом √a или a^(1/2).

Кубический корень числа a равен числу b, при котором b^3 = a. Кубический корень обозначается символом ∛a или a^(1/3).

Для нахождения корня числа обычно используется калькулятор или математическое программное обеспечение. Однако, в некоторых случаях можно использовать методы приближенного вычисления корня числа.

Что такое корень числа?

Корень числа обозначается символом √. Если у нас есть число a и мы ищем корень степени n, то запись будет выглядеть так: √a.

Например, корень числа 9 будет обозначаться как √9.

Корень числа можно найти с помощью различных методов, таких как методы приближения или использование специальных формул. Один из самых простых способов найти корень числа – это использовать квадратный корень.

Квадратный корень – это корень степени 2. Если нам нужно найти квадратный корень числа a, то мы ищем число, которое при возведении в степень 2 даст нам число a. Квадратный корень числа a обозначается как √a или a1/2.

Например, квадратный корень числа 16 будет выглядеть так: √16 = 4.

Корень числа – важное понятие в математике и находит применение в различных областях, таких как физика, экономика, инженерия и других науках. Знание, как найти корень числа, позволяет решать разнообразные задачи и применять математические методы в реальной жизни.

Вопрос-ответ:

Как найти корень числа?

Для того чтобы найти корень числа, нужно возвести это число в степень, которая будет равна обратной степени корня.

Как вычислить квадратный корень числа?

Для того чтобы вычислить квадратный корень числа, нужно найти число, которое при возведении в квадрат даст исходное число.

Как вычислить корень числа с помощью калькулятора?

Для вычисления корня числа с помощью калькулятора нужно нажать на кнопку «корень» или «sqrt», затем ввести число и нажать на кнопку «равно».

Как найти кубический корень числа?

Для того чтобы найти кубический корень числа, нужно найти число, которое при возведении в куб даст исходное число.

Как найти корень числа вручную?

Для вычисления корня числа вручную можно использовать метод Ньютона. Этот метод заключается в последовательном уточнении приближенного значения корня.

Как найти корень числа? Подробное объяснение, пожалуйста.

Для того чтобы найти корень числа, нужно использовать операцию извлечения корня. Корень числа является таким числом, при возведении в квадрат которого получается исходное число. Для нахождения корня числа можно использовать различные методы, такие как метод бинарного поиска или метод Ньютона. При использовании метода бинарного поиска, мы выбираем начальный интервал, в котором находится искомый корень, затем на каждом шаге делим интервал пополам и проверяем, к какой половине интервала относится корень. При использовании метода Ньютона, мы выбираем начальное приближение корня и последовательно уточняем его, используя формулу: Xn+1 = (Xn + (a / Xn)) / 2, где Xn — текущее приближение корня, а — исходное число. После нескольких итераций получаем более точное приближение корня числа.

Как найти корень числа с помощью метода Ньютона? Можно привести пример?

Для нахождения корня числа с помощью метода Ньютона, нужно выбрать начальное приближение корня и последовательно уточнять его, используя формулу: Xn+1 = (Xn + (a / Xn)) / 2, где Xn — текущее приближение корня, а — исходное число. Пример: найдем корень числа 9 с точностью до трех знаков после запятой. Возьмем начальное приближение X0 = 3. Подставляем его в формулу: X1 = (3 + (9 / 3)) / 2 = 2.5. Затем повторяем этот шаг до достижения необходимой точности. В данном случае, после нескольких итераций получаем приближенное значение корня числа 9, равное 3.000.

Как найти корень числа?

Один из самых популярных методов приближенного нахождения корня числа — метод Ньютона. Для его использования необходимо выбрать начальное приближение, а затем с помощью рекуррентной формулы приближенно находить следующие значения, приближаясь к корню числа.

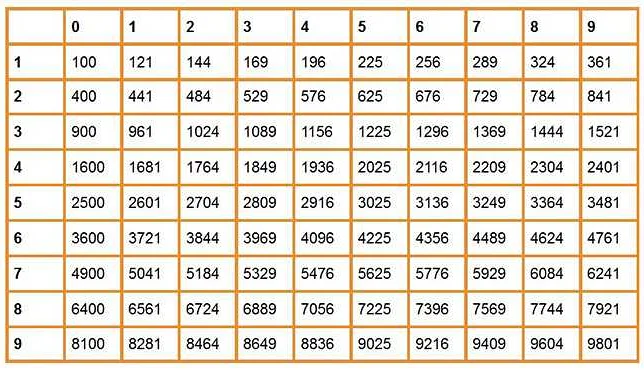
Метод точного вычисления корня числа включает в себя использование математических функций или таблиц со значениями корней чисел. Например, для нахождения квадратного корня числа можно воспользоваться функцией sqrt() в языке программирования или таблицей с предварительно вычисленными значениями корней.

В таблице ниже приведены примеры вычисления корня числа:

ЧислоКорень

25	5
36	6
49	7

Таким образом, для нахождения корня числа необходимо использовать методы приближенного нахождения корня или методы точного вычисления корня с помощью математических функций или предварительно вычисленных значений.

Методы нахождения корня

Существует несколько методов нахождения корня числа. Рассмотрим некоторые из них:

1. Метод проб и ошибок. Этот метод заключается в последовательной проверке всех чисел от 1 до искомого корня. Если произведение числа на само себя равно исходному числу, то это искомый корень. Например, чтобы найти корень числа 16, мы начинаем с 1 и проверяем: 1*1=1, 2*2=4, 3*3=9, 4*4=16. Таким образом, корень числа 16 равен 4.

2. Метод деления интервала пополам. Этот метод основан на принципе бинарного поиска. Начинаем с определения интервала, в котором находится искомый корень, например, от 0 до исходного числа. Затем делим этот интервал пополам и проверяем, в какой половине находится корень. Если произведение числа на само себя больше исходного числа, то корень находится в левой половине интервала, иначе в правой половине. После каждой итерации интервал сужается, пока не достигнем требуемой точности. Например, для нахождения корня числа 16, мы начинаем с интервала от 0 до 16 и проверяем: 8*8=64 (корень в левой половине), затем интервал сужается до 0-8 и проверяем: 4*4=16. Таким образом, корень числа 16 равен 4.

3. Метод Ньютона. Этот метод основан на использовании производной функции. На каждой итерации вычисляется значение функции и ее производной в текущей точке и используется для приближенного нахождения корня. Этот метод требует знания функции, для которой ищется корень, и его производной. Например, для нахождения корня числа 16 можно использовать функцию f(x) = x^2 — 16 и ее производную f'(x) = 2x. Начинаем с некоторого начального приближения, например, x = 8. Затем на каждой итерации используем формулу x = x — (f(x) / f'(x)) для приближенного вычисления корня. После нескольких итераций получаем значение близкое к истинному значению корня. В данном примере, после нескольких итераций получаем, что корень числа 16 равен примерно 4.

Как использовать калькулятор для поиска корня числа

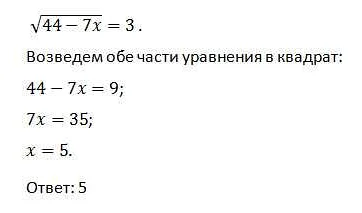
Чтобы найти корень числа, необходимо ввести число, а затем нажать на кнопку с символом корня или функцией «корень» на калькуляторе. Далее калькулятор автоматически выполнит операцию и покажет результат на дисплее.

Например, для нахождения квадратного корня из числа 16, следует ввести число 16 на калькуляторе и нажать на кнопку с символом корня. Калькулятор выведет результат — число 4, так как 4 умноженное на себя даёт 16.

Также можно использовать калькулятор для нахождения корня числа, отличного от квадратного. Для этого следует использовать функцию «корень» или «sqrt» на калькуляторе и указать степень корня.

Например, для нахождения кубического корня из числа 27, следует ввести число 27 на калькуляторе и выбрать функцию «корень». Затем указать степень 3, так как кубический корень из числа — это число, возведенное в степень 3. Калькулятор выведет результат — число 3, так как 3 умноженное на себя два раза даёт 27.

Таким образом, калькулятор является удобным инструментом для нахождения корня числа. Он позволяет быстро и точно выполнить операцию и получить результат.

Примеры нахождения корня числа

Для наглядности рассмотрим несколько примеров нахождения корня числа:

Пример 1: Найти квадратный корень числа 9.

Решение: Квадратный корень числа 9 равен 3, так как 3 * 3 = 9.

Пример 2: Найти кубический корень числа 27.

Решение: Кубический корень числа 27 равен 3, так как 3 * 3 * 3 = 27.

Пример 3: Найти корень числа 16.

Решение: Корень числа 16 равен 4, так как 4 * 4 = 16.

Пример 4: Найти корень числа 625.

Решение: Корень числа 625 равен 25, так как 25 * 25 = 625.

Пример 5: Найти корень числа 2.

Решение: Корень числа 2 является иррациональным числом, которое можно приближенно выразить как 1,414213562.

Корень числа в реальной жизни

Одно из применений корня числа в реальной жизни — нахождение квадратного корня. Например, при строительстве зданий и сооружений необходимо знать длину стороны квадрата, чтобы правильно расположить материалы и рассчитать его площадь. Для этого можно использовать квадратный корень, который позволяет найти длину стороны, зная площадь.

Другим примером использования корня числа является расчет процентного прироста. Например, при анализе финансовых показателей компании инвесторы и аналитики часто смотрят на годовой прирост доходов. Для расчета процентного прироста можно использовать корень числа, чтобы найти значение прироста, зная начальное и конечное значение.

Корень числа также применяется в физике для решения различных задач. Например, при расчете скорости движения тела или при определении времени, необходимого для достижения определенного расстояния, может потребоваться использование корня числа.

В общем, понимание и использование корня числа является важным навыком, который может быть полезен во многих сферах жизни. Знание этой математической операции позволяет решать различные задачи и делать более точные вычисления.

Применение корня числаПример

Строительство	Нахождение длины стороны квадрата по известной площади
Финансы	Расчет процентного прироста
Физика	Расчет скорости или времени