Что такое мера математика
Содержимое
Мера в математике является понятием, используемым для измерения размера, объема или количества. Она определяет, каким образом можно измерить или оценить математический объект или его свойства. Мера может быть применена к различным объектам, таким как геометрические фигуры, функции, множества и т. д. Она является одной из основных концепций в математическом анализе и теории вероятностей.
Мера – это понятие, неотъемлемое от математики. Она используется для измерения различных характеристик объектов и событий. Мера позволяет описывать и сравнивать различные величины и устанавливать отношения между ними. В математике мера может быть применена к различным объектам, начиная от чисел и геометрических фигур, и заканчивая вероятностными распределениями и функциями.
Определение меры в математике основано на наборе аксиом и свойств. Она должна удовлетворять определенным критериям и иметь определенные свойства. Например, мера должна быть неотрицательной, то есть не может принимать отрицательных значений. Она также должна быть аддитивной, то есть для объединения нескольких непересекающихся множеств мера должна быть равна сумме мер каждого отдельного множества.
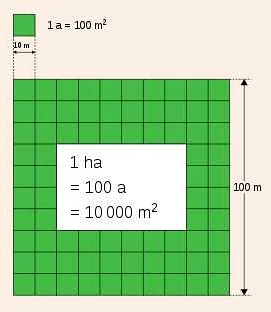
Примеры меры в математике включают длину, площадь, объем, массу, вероятность и многие другие. Например, длина может быть измерена в метрах или футах, площадь — в квадратных метрах или квадратных футах, а масса — в граммах или унциях. Мера также может быть связана с вероятностью, например, вероятность выпадения определенной стороны монеты или числа на игральной кости.
Определение меры в математике
Мера обладает несколькими важными свойствами:
- Неотрицательность: мера любого множества всегда неотрицательна. Мера никогда не может быть отрицательной числовой величиной.
- Нулевая мера пустого множества: мера пустого множества всегда равна нулю. Пустое множество не содержит элементов, поэтому его размер равен нулю.
- Аддитивность: если два множества не имеют общих элементов, то мера их объединения равна сумме мер каждого из множеств по отдельности. Это свойство называется аддитивностью меры.
Примеры мер в математике включают счетную меру, меру Лебега и меру вероятности. Счетная мера используется для подсчета количества элементов в счетном множестве, мера Лебега применяется для измерения длины, площади или объема множества, а мера вероятности используется в теории вероятностей для измерения вероятности наступления событий.
Свойства меры
1. Неотрицательность: Мера любого множества всегда неотрицательна. То есть, если A — множество, то мера множества A всегда больше или равна нулю.
2. Аддитивность: Если A и B — непересекающиеся множества, то мера их объединения равна сумме мер каждого из множеств. Формально это выражается следующим образом: если A и B — непересекающиеся множества, то мера (A ∪ B) = мера A + мера B.
3. Монотонность: Если A и B — множества, причем A содержится в B (A ⊆ B), то мера множества A меньше или равна мере множества B. Формально это выражается следующим образом: если A ⊆ B, то мера A ≤ мера B.
4. Счётная аддитивность: Если A1, A2, A3, … — попарно непересекающиеся множества, то мера их объединения равна сумме мер каждого из множеств. Формально это выражается следующим образом: если A1, A2, A3, … — попарно непересекающиеся множества, то мера (∪i Ai) = ∑i мера Ai.
5. Непрерывность снизу: Если A1 ⊆ A2 ⊆ A3 ⊆ …, то мера их объединения равна пределу мер каждого из множеств. Формально это выражается следующим образом: если A1 ⊆ A2 ⊆ A3 ⊆ …, то мера (∪i Ai) = limi→∞ мера Ai.
Эти свойства позволяют более удобно работать с мерой, делая ее более предсказуемой и позволяя получать новые результаты на основе уже известных.
Примеры меры

В математике существует множество примеров меры, которые используются для измерения различных свойств объектов и явлений.
Один из примеров — мера длины. Она используется для измерения длины отрезков, относительных расстояний и других объектов, имеющих одну измеряемую характеристику — длину.
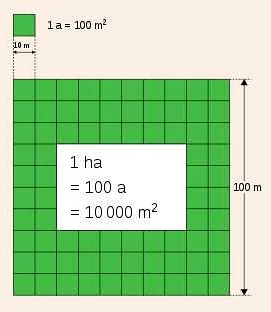
Другой пример — мера площади. Она позволяет измерять площади поверхностей, фигур и других объектов, имеющих двумерные характеристики.
Также существует мера объема, которая используется для измерения объема тел и пространственных объектов.
Еще один пример меры — мера вероятности. Она позволяет оценить вероятность наступления события и используется в теории вероятностей и математической статистике.
Меры также могут быть определены для различных абстрактных объектов, таких как множества и функции. Например, существуют меры на множествах, которые позволяют измерять их размер или степень содержания.
Тип мерыПримеры
| Мера длины | Метр, фут, миля |
| Мера площади | Квадратный метр, квадратный фут |
| Мера объема | Кубический метр, галлон |
| Мера вероятности | Относительная частота, вероятность события |
Это лишь некоторые примеры меры в математике. В реальном мире и в различных областях науки используются различные меры, в зависимости от того, что именно требуется измерить.
Счетно-аддитивная мера
Счетно-аддитивная мера задается на сигма-алгебре множеств и обладает двумя основными свойствами:
- Счетная аддитивность: если имеется счетное количество непересекающихся множеств, то мера их объединения равна сумме их мер.
- Монотонность: если одно множество вложено в другое, то его мера не превосходит меры вложенного множества.
Счетно-аддитивная мера является обобщением понятия вероятности на произвольные множества. Она позволяет измерять «размер» подмножеств, что является важной задачей в математике и других науках.
Примером счетно-аддитивной меры является классическая мера Лебега на прямой. Она определена на всех подмножествах прямой и измеряет их длину. Данная мера является счетно-аддитивной, так как для любого счетного набора непересекающихся интервалов их объединение будет иметь длину, равную сумме длин отдельных интервалов.
Счетно-аддитивная мера является важным инструментом в анализе, теории вероятностей и других областях математики. Она позволяет формально определить понятие «меры» и использовать его для изучения свойств множеств и функций.
Счетно-аддитивная мера и счетная аддитивность
Счетная аддитивность — это свойство меры, которое говорит о том, что мера объединения счетного числа непересекающихся множеств равна сумме мер каждого из этих множеств. То есть, если имеется счетное множество непересекающихся множеств A1, A2, A3, …, то мера их объединения равна сумме мер каждого из них: мера(A1 ∪ A2 ∪ A3 ∪ …) = мера(A1) + мера(A2) + мера(A3) + …
Счетно-аддитивная мера является более общим понятием, чем конечно-аддитивная мера. Она позволяет работать с бесконечными множествами и более сложными структурами. Это свойство делает ее удобной и широко применяемой в различных областях математики, физики и других наук.
Примером счетно-аддитивной меры может служить мера Лебега — основная мера в теории меры и интеграла. Она определена на классе борелевских множеств на прямой и обладает свойством счетной аддитивности.
МножествоМера
| A1 | 1 |
| A2 | 2 |
| A3 | 3 |
| … | … |
Таким образом, мера объединения всех этих множеств будет равна 1 + 2 + 3 + … = ∞. Это характеризует свойство счетной аддитивности меры Лебега.
Непрерывность меры
Формально, пусть даны множества A и B, причем A включено в B. Тогда, если мера множества A равна a и мера множества B равна b, то мера объединения множеств A и B равна a + (b — a), или, что равносильно, равна b.
То есть, если имеется последовательность множеств A1, A2, A3, …, таких, что каждое следующее множество An+1 содержит предыдущее множество An, то мера объединения всех этих множеств будет равна сумме мер каждого из них.
Непрерывность меры является важным свойством, которое позволяет использовать меру для измерения сложных объектов и наборов.
Видео по теме:
Вопрос-ответ:
Что такое мера в математике?
Мера в математике — это функция, которая присваивает некоторым подмножествам заданного множества числа, называемые «мерой». Мера используется для измерения размера, объема или вероятности некоторого объекта.
Какие свойства имеет мера в математике?
Мера обладает несколькими важными свойствами. Во-первых, мера никогда не может быть отрицательной. Кроме того, если объединение непересекающихся подмножеств равно всему множеству, то мера объединения равна сумме мер этих подмножеств. Наконец, если одно множество является подмножеством другого, то мера подмножества не может быть больше меры супермножества.
Какие примеры можно привести для меры в математике?
Примерами меры в математике являются, например, длина, площадь и объем. Для одномерного пространства мерой может быть длина отрезка, для двумерного — площадь фигуры, а для трехмерного — объем тела. Также мерой может быть вероятность, которая измеряет вероятность наступления события.
Какие еще свойства меры существуют?
Помимо основных свойств, мера также обладает другими характеристиками. Например, если мера пустого множества равна нулю, то мера множества, состоящего из одной точки, равна нулю. Также мера неизменна при параллельном переносе множества и не зависит от его положения в пространстве.
Какую роль играет мера в математике?
Мера играет важную роль в математике, так как позволяет измерять и описывать различные объекты и явления. Она помогает определить размеры и свойства множества, а также решать задачи, связанные с вероятностью и статистикой. Без меры было бы сложно оценивать и сравнивать различные объекты и их свойства.
Что такое мера в математике?
Мера в математике — это концепция, которая используется для измерения размера, объема или длины некоторого объекта или события. Она позволяет математикам определить количество элементов в множестве или оценить вероятность наступления определенного события. Мера может быть применена к различным объектам, таким как геометрические фигуры, непрерывные функции или вероятностные пространства.
Абсолютная мера
В отличие от относительной меры, абсолютная мера не зависит от других объектов или множеств, а определяется самим объектом или множеством. Это означает, что абсолютная мера описывает только сам объект и не учитывает его отношение к другим объектам или множествам.
Абсолютная мера может быть применена к различным объектам и множествам. Например, абсолютная мера может быть использована для измерения длины прямой или площади плоскости. Она также может быть применена для измерения объема тела или массы предмета.
Важной особенностью абсолютной меры является ее свойство сохранения. Это означает, что при перемещении объекта или множества абсолютная мера остается неизменной. Например, если мы переместим прямую на плоскости, ее длина будет оставаться неизменной, так как абсолютная мера длины сохраняется.
Примером абсолютной меры может служить метрическая система измерений, где длина измеряется в метрах, площадь — в квадратных метрах, а объем — в кубических метрах. В этом случае абсолютная мера определяется самими единицами измерения и не зависит от других факторов.
Связь меры с интегралом

Если задано измеримое множество X и функция f(x), определенная на этом множестве, то интеграл от функции f(x) на множестве X можно вычислить следующим образом:
Определенный интегралНесобственный интеграл
| $$\int_{X} f(x) \,dx$$ | $$\int_{a}^{b} f(x) \,dx$$ |
Мера множества X может быть определена как:
Мера множества XОбъем множества X
| $$\mu(X)$$ | $$\text{vol}(X)$$ |
Связь меры с интегралом заключается в том, что если функция f(x) интегрируема на множестве X, то интеграл от функции f(x) на множестве X равен мере множества X, умноженной на среднее значение функции на этом множестве:
$$\int_{X} f(x) \,dx = \mu(X) \cdot \frac{1}{\mu(X)} \int_{X} f(x) \,dx$$
Таким образом, мера и интеграл позволяют описывать и измерять свойства множества и функции в математике.



Статья очень интересная и полезная! В ней очень понятно и подробно описано, что такое мера в математике. Я давно слышала этот термин, но не всегда могла понять его значение. Благодаря этой статье, я наконец-то разобралась! Очень понравилось, как автор объяснил определение меры. Он сказал, что это числовая характеристика, которая позволяет измерить длину, площадь, объем и другие характеристики объектов. Теперь мне стало понятно, каким образом ученые измеряют различные величины в математике. Также в статье были описаны свойства меры. Интересно узнать, что мера должна быть неотрицательной, а также удовлетворять условию единственности и аддитивности. Эти свойства помогают ученым проводить точные измерения и делать правильные выводы на основе полученных данных. Автор также привел несколько примеров, чтобы проиллюстрировать применение меры в математике. Он рассказал о том, как можно измерить длину отрезка, площадь прямоугольника и объем параллелепипеда. Эти примеры помогли мне лучше понять, каким образом мера используется на практике. В целом, статья очень понятно и доступно объясняет, что такое мера в математике. Благодаря этому материалу, я теперь лучше понимаю, как ученые измеряют различные величины и каким образом математика применяется в повседневной жизни. Рекомендую эту статью всем, кто интересуется математикой и хочет углубить свои знания в этой области.
Математика всегда казалась мне сложной дисциплиной, но последнее время я начала осознавать, что ее основы могут быть довольно интересными и применимыми в повседневной жизни. Одним из таких основных понятий является мера. Мера в математике – это способ определить размер или количество объектов. Это такая шкала, которая помогает нам измерять и сравнивать различные величины. Например, длина, площадь, объем – все это можно измерить с помощью меры. Одна из основных свойств меры – это ее неотрицательность. Мера всегда будет неотрицательной величиной, поскольку она определяет размер или количество, которое не может быть отрицательным. Также мера обладает свойством аддитивности. Это значит, что если мы хотим измерить сумму двух объектов, мы можем просто сложить их меры. Например, если у нас есть два отрезка, то сумма их длин будет равна сумме длин каждого отрезка отдельно. Чтобы лучше понять это понятие, рассмотрим пример. Представим, что у нас есть несколько книг разного размера. Мы можем измерить их размеры с помощью меры – длины, ширины и высоты. Затем мы можем сложить эти размеры и получить общую меру книги. Таким образом, мы можем сравнить размеры разных книг и определить, какая из них больше или меньше. Мера в математике играет важную роль во многих областях, в том числе и в физике, экономике и статистике. Она позволяет нам измерять и описывать различные явления и является основой для многих математических моделей. Таким образом, понимание меры в математике помогает нам более точно оценивать и анализировать окружающий нас мир. Это понятие является основой для измерения различных величин и имеет широкое применение в нашей повседневной жизни.
Мера — это одно из фундаментальных понятий математики, которое позволяет измерять и описывать различные объекты и явления. Она выражает количество, степень или интенсивность того или иного свойства. Мера имеет свои особенности и свойства, которые делают ее уникальной и полезной в математическом анализе. Во-первых, мера должна быть неотрицательной, то есть ее значение не может быть отрицательным. Во-вторых, она должна быть аддитивной, что означает, что мера объединения двух непересекающихся множеств равна сумме мер каждого из них. Наконец, мера должна быть нормированной, то есть мера пустого множества равна нулю. Примером меры может служить понятие длины на прямой. Длина отрезка равна разности координат его концов. Это соответствует всем свойствам, которые были описаны ранее. Например, длина объединения двух непересекающихся отрезков будет равна сумме их длин. В математике мера играет важную роль в теории вероятностей, геометрии, анализе и других областях. Она позволяет формализовать и анализировать различные явления и свойства объектов, что делает ее необходимой в научных исследованиях. Таким образом, мера — это мощный инструмент математики, который позволяет измерять и анализировать различные объекты и явления. Ее свойства и определение делают ее полезной и универсальной в различных областях.
В этой статье очень хорошо изложено все, что нужно знать о мере в математике. Я, как студент, всегда пытаюсь разобраться в этих сложных темах, и эта статья помогла мне лучше понять суть меры и ее свойства. Мера — это понятие, которое используется в математике для измерения размера или объема некоторого множества. Она позволяет нам определить, насколько «большим» или «маленьким» является это множество. Одним из главных свойств меры является ее неотрицательность: мера любого множества всегда больше или равна нулю. Это логично, ведь мера измеряет размер, и размер не может быть отрицательным. Также стоит отметить, что мера обладает свойством аддитивности. Это значит, что если мы разделяем множество на несколько непересекающихся подмножеств, то мера всего множества будет равна сумме мер этих подмножеств. Например, если мы имеем множество точек на плоскости, и мы разделяем его на два непересекающихся подмножества, то мера всего множества будет равна сумме мер этих двух подмножеств. Примерами меры могут быть обычная длина, площадь, объем и т.д. Они позволяют нам определить размеры различных геометрических фигур и объектов в пространстве. Например, мы можем измерить длину отрезка, площадь круга или объем параллелепипеда с помощью меры. В общем, я очень доволен этой статьей. Она ясно и понятно объясняет, что такое мера в математике и как она работает. Благодаря ей я лучше понимаю эту сложную тему и могу применять ее знания в своих учебных заданиях и задачах.