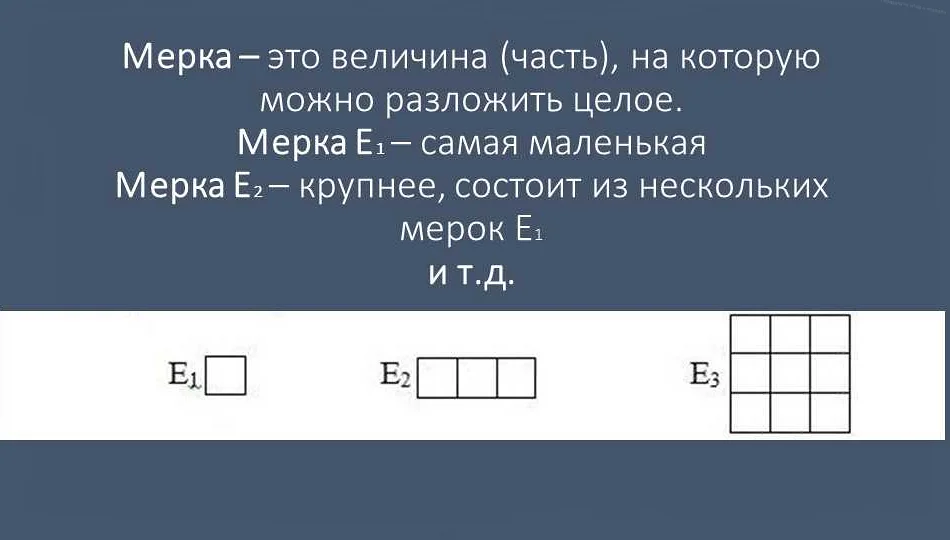
Что такое мерка в математике

Мерка в математике — это понятие, которое обозначает меру, или размер, объекта или пространства. Она используется для измерения различных параметров, таких как длина, площадь, объем и другие. В математических моделях и задачах, мерка играет важную роль, позволяя точно определить и сравнивать величины и свойства различных объектов и пространств.

В математике понятие мерки играет важную роль при измерении и сравнении объектов. Мерка – это числовое значение или стандарт, которым можно измерять или оценивать различные характеристики предметов или явлений. Она позволяет определить количество или качество объекта и сравнить его с другими объектами.

В математике существуют различные типы мерок, которые применяются в разных областях: длина, площадь, объем, масса и так далее. Например, метр – это мерка длины, килограмм – мерка массы, кубический метр – мерка объема. Каждая мерка имеет свои единицы измерения, которые определяются стандартами.

Мерка также используется для сравнения и установления отношений между объектами. Например, при измерении длин можно сравнить два отрезка и определить, какой из них длиннее или короче. Также мерка позволяет сравнивать объекты по их качественным характеристикам. Например, мерка массы позволяет определить, какой объект тяжелее или легче другого.

Мерка является важным инструментом для математического моделирования, изучения явлений природы, а также для решения практических задач в различных областях жизни.

Важно отметить, что мерка имеет свои ограничения и может быть применима только в определенных контекстах. Например, мерка времени может быть не применима для измерения расстояния. Поэтому при использовании мерки необходимо учитывать контекст и выбирать соответствующую мерку и единицы измерения.

Мерка в математике: определение и применение

Мерка позволяет измерять и сравнивать различные величины, а также проводить операции с ними, такие как сложение, вычитание, умножение и деление.

Одно из самых простых и распространенных применений мерки – измерение длины. Например, если нужно измерить длину отрезка, то величину этой длины можно выразить в метрах, сантиметрах, километрах и т.д. В этом случае мерка показывает, сколько раз нужно взять единицу измерения (например, метр) для того, чтобы измерить данную величину.

Мерка также применяется в геометрии для измерения площади фигур. Например, чтобы найти площадь прямоугольника, нужно умножить длину одной стороны на длину другой стороны. В этом случае мерка показывает, сколько квадратных единиц нужно для того, чтобы покрыть всю поверхность фигуры.

Кроме того, мерка используется в физике для измерения объема тела или жидкости. Например, чтобы найти объем куба, нужно умножить длину каждой его стороны. В этом случае мерка показывает, сколько кубических единиц нужно для заполнения всего объема тела.

Таким образом, мерка является важным инструментом для измерения различных величин и проведения математических операций. Она позволяет нам точно определить и сравнить объекты в пространстве и времени, а также решать задачи и проблемы, связанные с количественными характеристиками.

Видео по теме:

Основные понятия

Существует несколько основных понятий, связанных с мерками:

1. Измерение: процесс определения числового значения с помощью мерки. Например, измерение длины отрезка с помощью линейки.
2. Единица измерения: определенное значение, используемое для измерения. Например, метр — единица измерения длины.
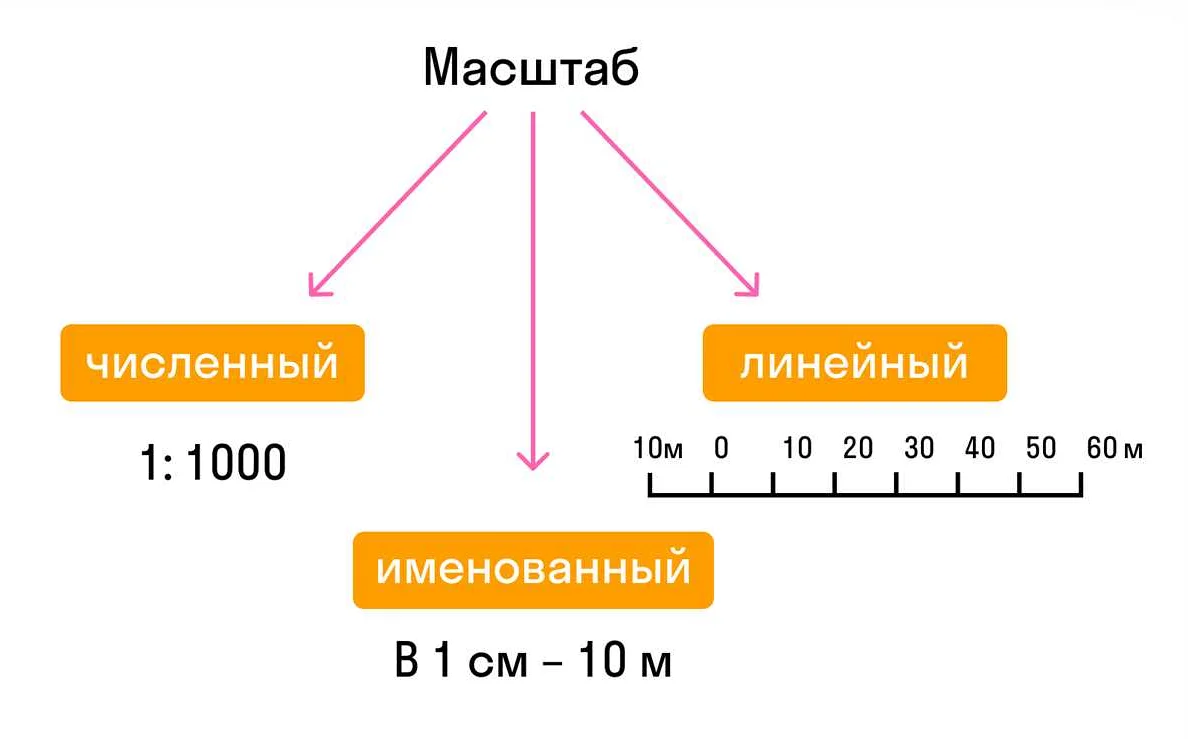
3. Масштаб: соотношение между значением измерения и его представлением на диаграмме или карте. Например, масштаб 1:100 означает, что 1 сантиметр на диаграмме соответствует 100 сантиметрам в реальности.
4. Точность: степень детализации измерения или представления значения. Например, измерение длины с точностью до миллиметра.
5. Нормализация: процесс приведения значения к определенному диапазону или единице измерения. Например, приведение времени к стандартному формату часы:минуты:секунды.

Понимание основных понятий связанных с мерками позволяет более точно и удобно работать с измерениями и вычислениями в математике.

Свойства мерки

1. Свойство неотрицательности: Мера любого подмножества множества неотрицательна. Это означает, что мера не может быть отрицательной числом.

2. Свойство аддитивности: Если два подмножества множества не пересекаются, то мера их объединения равна сумме их мер. Формально это записывается как: если A и B — не пересекающиеся подмножества, то мера (A ∪ B) = мера A + мера B.

3. Свойство монотонности: Если одно подмножество является подмножеством другого, то мера меньшего подмножества не превосходит меру большего. Формально это записывается как: если A ⊆ B, то мера A ≤ мера B.

4. Свойство счетной аддитивности: Если имеется счетное количество попарно непересекающихся подмножеств A₁, A₂, A₃,…, то мера их объединения равна сумме их мер. Формально это записывается как: если A₁, A₂, A₃,… — попарно непересекающиеся подмножества, то мера (A₁ ∪ A₂ ∪ A₃ ∪ …) = мера A₁ + мера A₂ + мера A₃ + …

5. Свойство нормированности: Мера пустого множества равна нулю. Формально это записывается как: мера ∅ = 0.

Эти свойства мерки помогают определить и использовать меру для измерения объемов, площадей, вероятностей и других характеристик объектов в математике.

Типы мерок

В математике существует несколько типов мерок, которые используются для измерения различных величин и объектов. Рассмотрим некоторые из них:

1. Линейные мерки: используются для измерения длины или расстояния между точками или объектами. Примером линейной мерки может служить метр или фут.
2. Площадные мерки: применяются для измерения площади поверхности, занимаемой объектом. Например, квадратный метр или квадратный фут.
3. Объемные мерки: используются для измерения объема тела или пространства. Например, кубический метр или кубический фут.
4. Массовые мерки: применяются для измерения массы или веса объектов. Примером массовой мерки может служить килограмм или фунт.
5. Временные мерки: используются для измерения времени. Например, секунда или минута.
6. Угловые мерки: применяются для измерения углов. Примером угловой мерки может служить градус или радиан.

Каждая из этих мерок имеет свои характеристики и правила использования. Знание и понимание различных типов мерок позволяет математикам и другим специалистам в различных областях применять их в своей работе и исследованиях.

Применение мерок

Мерки широко применяются в математике для измерения различных величин. Они могут использоваться для определения длины, площади, объёма, массы и других физических величин.

Одна из наиболее распространённых мерок — метрическая система. В ней используются такие единицы измерения, как метр, килограмм, секунда и другие. Метрическая система основана на десятичной системе счисления, что делает её удобной и легкой в использовании.

Более специализированные мерки применяются в различных областях науки и техники. Например, в физике для измерения электрической силы используется единица вольт, а для измерения силы тока — ампер. В химии применяются мерки для измерения концентрации вещества, такие как моль и грамм на литр.

Кроме того, в математике мерки могут быть использованы для измерения геометрических фигур и фигур в пространстве. Например, для измерения длины отрезка используется мерка в виде числа, обозначающего количество единичных отрезков. Для измерения площади применяется мерка в виде квадратных единиц, а для измерения объёма — кубических единиц.

Важно уметь выбирать подходящую мерку для измерения каждой конкретной величины. Правильное применение мерки способствует корректному и точному измерению и анализу данных, что является важным во многих областях науки и техники.

Измерение и сравнение

Измерение является процессом определения числовой характеристики объекта с использованием мерки. Например, для измерения длины можно использовать мерку в виде линейки, шкалы или мерной ленты. Путем размещения мерки на объекте и определения числового значения, можно узнать его длину.

Сравнение с помощью мерки позволяет определить, какое из двух объектов имеет большую или меньшую величину свойства. Например, с помощью мерки в виде весов можно сравнить массу двух предметов и определить, какой из них тяжелее или легче.

Для удобства сравнения величин, мерки могут быть разделены на равные части с помощью делений или шкал. Это позволяет установить соотношение между объектами и определить их порядок. Например, с помощью мерки в виде десятичной линейки можно определить, что один отрезок длиной 5 см меньше, чем отрезок длиной 7 см.

Измерение и сравнение с помощью мерок являются важными понятиями в математике, которые используются для решения различных задач и проведения исследований. Они позволяют установить точные значения величин и сравнить их между собой, что является основой для дальнейших математических операций и выводов.

Мерка в геометрии

Одной из наиболее распространенных единиц измерения в геометрии является метрическая система, в которой длина измеряется в метрах, площадь – в квадратных метрах, а объем – в кубических метрах. Однако, в геометрии также используются и другие системы единиц, например, английская система, где длина измеряется в футах, дюймах и т.д.

Применение мерки в геометрии позволяет точно определять размеры и свойства геометрических фигур. С помощью мерки можно вычислить длину отрезка, площадь треугольника, объем параллелепипеда и т.д. Мерка также позволяет сравнивать различные фигуры и определять их соотношения, например, установить, какой из двух треугольников больше или меньше по площади.

Мерка в алгебре

Мерка обычно определяется на основе функции, называемой мерой. Мера — это функция, которая ставит в соответствие каждому подмножеству некоторого множества действительных чисел либо конечное число, либо плюс или минус бесконечность.

Мерка может иметь различные свойства, в зависимости от применяемого определения. Некоторые из них включают аддитивность, счетную аддитивность и непрерывность сверху. Аддитивность означает, что мера объединения двух непересекающихся множеств равна сумме мер этих множеств. Счетная аддитивность означает, что мера объединения счетного числа непересекающихся множеств равна сумме мер этих множеств. Непрерывность сверху означает, что мера монотонно возрастает при добавлении новых элементов в множество.

Мерки широко используются в различных областях алгебры, таких как теория вероятностей, анализ и множественный анализ данных. Они позволяют формализовать и измерить различные характеристики объектов и явлений, что делает их полезными инструментами для решения различных задач.

Вопрос-ответ:

Что такое мерка в математике?

Мерка в математике — это способ измерения и оценки различных характеристик объектов или явлений. Она позволяет численно выразить определенные свойства и отношения между ними. Мерка может быть определена для различных предметов и областей математики, таких как геометрия, алгебра, теория вероятностей и другие.

Какие основные виды мерок существуют в математике?

В математике существует несколько основных видов мерок, включая длину, площадь, объем, массу, время, скорость и т.д. Каждый вид мерки имеет свои единицы измерения и способы вычисления. Например, для измерения длины используется единица измерения метр, а для измерения времени — секунда.

Какие примеры применения мерок в математике?

Мерки широко применяются в математике для решения различных задач и изучения свойств объектов. Например, с помощью мерок можно вычислить площадь прямоугольника или треугольника, определить объем куба или сферы, рассчитать скорость движения объекта и т.д. Они также используются для проведения экспериментов и исследований в различных областях науки, таких как физика, химия и экономика.

Какие еще понятия связаны с мерками в математике?

С мерками в математике связаны такие понятия, как единицы измерения, точность измерения, масштаб, метрическая система, а также различные формулы и алгоритмы для выполнения вычислений. Кроме того, мерки имеют важное значение в понятиях сравнения и отношения между различными объектами или явлениями.