Что такое величина в математике 4

Величина в математике 4 — это числовое или символическое значение, которое может быть измерено или использовано для выполнения математических операций. Узнайте, как определить и использовать величины в математике 4 и как они связаны с другими математическими концепциями.

Величина – основной понятийный элемент в математике. Она представляет собой абстрактный объект, который можно измерять и сравнивать с другими объектами. Величины являются фундаментальными для математического анализа и представляют собой основу для многих других математических концепций и теорий.

Величины могут быть различной природы – от физических объектов, таких как время, длина или масса, до абстрактных понятий, таких как числа или функции. Они могут быть представлены числами, символами или формулами, в зависимости от того, какую информацию они представляют. Величины могут быть как дискретными, принимающими конечное или счетное множество значений, так и непрерывными, принимающими любое значение из некоторого интервала.

Свойства величин в математике тесно связаны с операциями, которые можно выполнять над ними. Например, для величин можно выполнять арифметические операции, такие как сложение, вычитание, умножение и деление. Кроме того, величины могут быть сравнимы друг с другом, что позволяет устанавливать отношения порядка между ними.

Примеры величин в математике включают числа, такие как целые числа, вещественные числа и комплексные числа, а также физические величины, такие как скорость, площадь и объем. Они играют важную роль в решении математических задач и моделировании реальных явлений. Понимание величин и их свойств является основой для более глубокого изучения математики и ее применения в различных областях науки и техники.

Величина в математике 4: определение, свойства и примеры

Величины в математике могут быть разделены на две основные категории: дискретные и непрерывные. Дискретные величины принимают отдельные значения из определенного множества, например, количество студентов в классе или число автомобилей на парковке. Непрерывные величины, напротив, могут принимать любое значение в определенном интервале, например, время или длина.

Величины могут обладать различными свойствами, которые помогают в их анализе и сравнении. Некоторые из основных свойств величин включают:

• Положительность: величина может быть положительной или неотрицательной, то есть иметь значение больше или равное нулю.
• Отрицательность: величина может быть отрицательной или неположительной, то есть иметь значение меньше или равное нулю.
• Абсолютная величина: абсолютная величина показывает расстояние от нуля до значения величины, независимо от ее знака. Например, абсолютная величина числа -5 равна 5.
• Сложение и вычитание: величины можно складывать и вычитать, получая новые значения.
• Умножение и деление: величины можно умножать и делить, получая новые значения.

Примеры величин в математике могут быть разнообразными. Например, количество денег на счету в банке, температура окружающей среды, скорость движения тела, масса предмета и т. д. Величины играют важную роль в математике и науке, позволяя измерять, описывать и анализировать различные явления и объекты.

Что такое величина в математике

Величины могут быть различных типов, например, числовыми или геометрическими. Числовые величины представляют собой числа, которые могут быть измерены или выражены в определенных единицах измерения. Геометрические величины, например, длина или площадь, связаны с геометрическими формами и могут быть измерены в соответствующих единицах измерения.

Величины могут иметь различные свойства, такие как величина и направление, положительное или отрицательное значение, а также абсолютное или относительное значение. Некоторые величины могут быть представлены в виде графиков или диаграмм для наглядного представления данных.

Примеры величин в математике включают время, расстояние, скорость, массу, температуру, площадь и объем. Эти величины могут быть измерены и использованы для решения различных задач и проблем в науке и повседневной жизни.

Определение величины

Величины могут быть различных типов, таких как физические величины (например, длина, время, скорость), математические величины (например, числа, векторы, матрицы) или другие абстрактные концепции (например, вероятность, масса, плотность).

Основные свойства величин:

1. Величины могут быть измерены или выражены числами.
2. Величины могут быть сравниваемы между собой.
3. Величины могут быть оперированы математическими операциями, такими как сложение, вычитание, умножение и деление.

Определение величины является основой для построения математических моделей и решения различных задач в науке, технике, экономике и других областях знания.

Свойства величин в математике

Величины в математике обладают рядом свойств, которые позволяют проводить различные операции с ними и рассчитывать их характеристики. Вот некоторые из основных свойств величин:

• Сложение и вычитание: Величины можно складывать и вычитать, результатом будет новая величина, которая будет зависеть от значений исходных величин.
• Умножение и деление: Величины также можно умножать и делить друг на друга. Результатом будет новая величина, которая будет зависеть от значений исходных величин.
• Ассоциативность: Порядок выполнения операций с величинами не влияет на результат. Например, при сложении нескольких величин можно менять порядок слагаемых, результат останется неизменным.
• Коммутативность: Порядок величин не влияет на результат операций. Например, при сложении нескольких величин можно менять их местами, результат останется неизменным.
• Дистрибутивность: При выполнении операций умножения и сложения величин можно менять порядок их выполнения без изменения результата.

Эти свойства величин позволяют математикам проводить различные манипуляции с числами, а также применять их в различных областях науки и техники.

Примеры величин

Величины в математике могут представлять различные параметры и характеристики объектов или процессов. Вот несколько примеров величин:

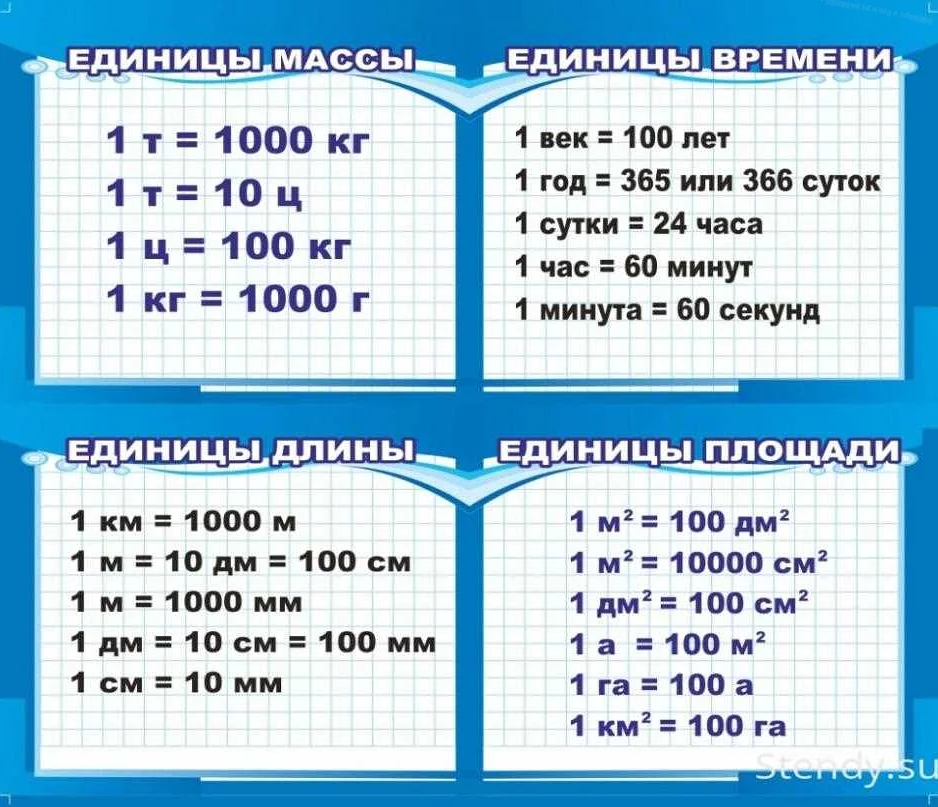
1. Длина: это одна из основных величин, которая измеряет протяженность объекта. Например, длина отрезка, сторона прямоугольника или диагональ куба.
2. Масса: величина, которая показывает количество вещества, содержащегося в объекте. Измеряется в граммах, килограммах и т.д. Например, масса человека, масса предмета.
3. Время: величина, которая измеряет продолжительность события или процесса. Измеряется в секундах, минутах, часах и т.д. Например, время пути, время выполнения задачи.
4. Температура: величина, которая показывает холодно или тепло. Измеряется в градусах Цельсия или Фаренгейта. Например, температура воздуха, температура воды.
5. Площадь: величина, которая измеряет площадь поверхности объекта. Например, площадь квадрата, площадь круга.

Это только некоторые примеры величин. В математике существует множество других величин, которые могут быть использованы для описания различных аспектов объектов и явлений в нашем мире.

Классификация величин

Переменные величины представляют собой такие величины, которые могут принимать различные значения. Они могут изменяться в заданных пределах в зависимости от определенного фактора или условий. Примером переменной величины может служить время, температура, скорость, масса и т. д.

Постоянные величины, наоборот, имеют постоянное значение и не подвержены изменениям. Они остаются неизменными в течение определенного периода времени или в определенных условиях. Примерами постоянных величин могут служить числовые константы, такие как число Пи (π), число Наперова (е) и т. д.

Кроме того, величины могут также быть классифицированы по своей природе. В зависимости от этого, их можно разделить на физические и математические величины.

Физические величины связаны с измерением и характеристиками объектов и явлений реального мира. Они имеют физическую природу и свои единицы измерения. Примерами физических величин являются длина, масса, время, энергия и т. д.

Математические величины, в свою очередь, абстрактны и не связаны с реальными объектами или физическими явлениями. Они используются в математике для описания и решения различных задач. Примерами математических величин могут служить числа, алгебраические выражения, функции и т. д.

Категория величинПримеры

Переменные	Время, температура, скорость, масса
Постоянные	Число Пи (π), число Наперова (е)
Физические	Длина, масса, время, энергия
Математические	Числа, алгебраические выражения, функции

Математические операции с величинами

Основные математические операции, которые можно выполнять с величинами, включают:

1. Сложение. Операция сложения позволяет объединить две или более величины и получить их сумму. Например, если у нас есть две величины: 5 и 3, то их сумма будет равна 8.
2. Вычитание. Операция вычитания позволяет отнять одну величину от другой и получить разность. Например, если у нас есть две величины: 8 и 3, то их разность будет равна 5.
3. Умножение. Операция умножения позволяет увеличить значение величины на определенное число. Например, если у нас есть величина 4, а мы умножим ее на 3, то получим 12.
4. Деление. Операция деления позволяет разделить одну величину на другую и получить результат. Например, если у нас есть величина 12, а мы разделим ее на 3, то получим 4.

Математические операции с величинами могут использоваться в различных областях математики, физики, экономики и других наук. Они позволяют решать задачи, моделировать процессы и анализировать данные.

Важно помнить, что при выполнении математических операций с величинами необходимо учитывать их единицы измерения. Например, при сложении двух величин, имеющих разные единицы измерения, необходимо привести их к одной системе единиц, чтобы получить правильный результат.

В заключение, математические операции с величинами позволяют использовать математические методы для решения практических задач и получения новых знаний. Они являются одним из фундаментальных элементов математики и необходимы для работы с различными типами данных и величин.

Значение величины в математическом контексте

Величина в математике играет ключевую роль, поскольку она описывает количество или измерение объекта или явления. Значение величины представляет собой числовое выражение, которое связано с ней. Для удобства и точности измерения величин в математике используются единицы измерения.

Значение величины может быть абсолютным или относительным. Абсолютное значение величины представляет собой числовое выражение, не зависящее от других факторов. Например, длина отрезка 5 см является абсолютным значением величины. Относительное значение величины указывает на отношение одной величины к другой. Например, скорость автомобиля 60 км/ч является относительным значением величины, поскольку она указывает, на какое расстояние автомобиль может переместиться за один час.

Значение величины может быть измерено, вычислено или определено с использованием различных математических операций и методов. Например, для измерения длины можно использовать линейку или мерную ленту. Для вычисления площади прямоугольника можно использовать формулу S = a * b, где S — площадь, а и b — стороны прямоугольника.

Примеры значений величин в математическом контексте включают длину, площадь, объем, массу, скорость, время, температуру и т. д. Знание значений величин позволяет решать различные математические задачи, а также применять математические концепции и методы в реальной жизни.

ВеличинаЕдиница измеренияПример

Длина	Метр	5 м
Площадь	Квадратный метр	10 кв. м
Объем	Кубический метр	2 м3
Масса	Килограмм	500 г
Скорость	Метр в секунду	30 м/с
Время	Секунда	2 мин
Температура	Градус Цельсия	25 °C

Значение величины в реальной жизни

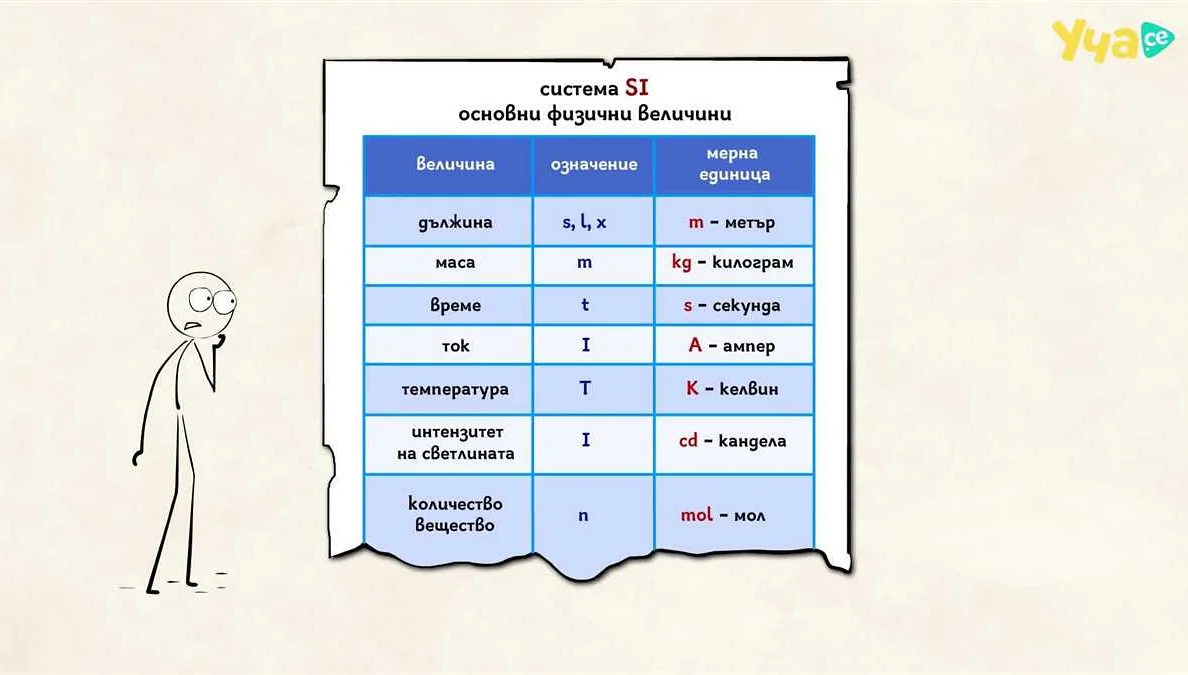
Величина в математике представляет собой числовую характеристику, которая используется для измерения, описания или сравнения объектов или явлений в реальном мире. Значение величины может быть выражено числом, единицей измерения или формулой.

В реальной жизни величины применяются в различных областях, таких как физика, химия, экономика, география и другие. Например, в физике величина времени используется для измерения длительности процессов или событий. Величина массы применяется для измерения количества вещества или объектов.

Значение величины также может быть использовано для сравнения различных объектов или явлений. Например, величина скорости позволяет сравнить скорость движения разных транспортных средств. Величина цены позволяет сравнить стоимость различных товаров или услуг.

Применение величин в реальной жизни помогает получить количественную информацию о мире вокруг нас, а также анализировать и предсказывать различные явления и процессы. Понимание значения величин и их правильное использование является важным навыком не только в математике, но и во многих других областях науки и повседневной жизни.

Вопрос-ответ:

Что такое величина в математике?

В математике величина — это числовое значение, которое может быть измерено или вычислено. Она может представлять собой любое количество или характеристику, которая может быть измерена или определена.

Какие свойства имеет величина в математике?

Величина в математике может иметь несколько свойств, включая аддитивное свойство (возможность сложения и вычитания), мультипликативное свойство (возможность умножения и деления) и транзитивное свойство (возможность сравнения и упорядочения).

Какие примеры величин существуют в математике?

В математике существует множество примеров величин. Например, длина, масса, время, скорость, площадь, объем, температура и др. Это только некоторые из множества величин, которые используются в математике для измерения и описания различных явлений и объектов.

Как определить и измерить величину в математике?

Величину в математике можно определить путем установления соответствующей шкалы измерения и единицы измерения. Например, для измерения длины можно использовать метры, для измерения массы — килограммы и т.д. Измерение величины осуществляется с помощью соответствующих инструментов или методов измерения, например, линейкой для измерения длины или весами для измерения массы.

Каким образом величины могут быть использованы в математике?

Величины могут быть использованы в математике для проведения различных вычислений, анализа данных, построения моделей и решения задач. Например, с помощью величин можно рассчитать площадь фигуры, определить среднее значение набора данных, моделировать движение объектов и т.д. Величины также могут быть использованы для сравнения и классификации объектов и явлений.

Видео по теме: