Что такое объем в математике 6 класс

Объем в математике 6 класс – это понятие, которое описывает трехмерное пространство, занимаемое телом. Статья рассказывает, как рассчитать объем различных фигур, таких как параллелепипед, пирамида и цилиндр, используя формулы и примеры. Узнайте, как правильно измерять и сравнивать объемы и как они связаны с понятием единицы объема. Познакомьтесь с простыми задачами на нахождение объема, которые помогут закрепить полученные знания и развить логическое мышление учеников 6 класса.

Объем – это одно из ключевых понятий в математике, которое широко используется в различных областях, включая геометрию и физику. В 6 классе учащиеся начинают изучать эту важную величину и осваивают базовые навыки ее расчета.

Объем – это мера пространства, занимаемого телом или фигурой. Он показывает, сколько места занимает объект в трехмерном пространстве. Объем измеряется в кубических единицах, таких как кубический сантиметр (см³) или кубический метр (м³).

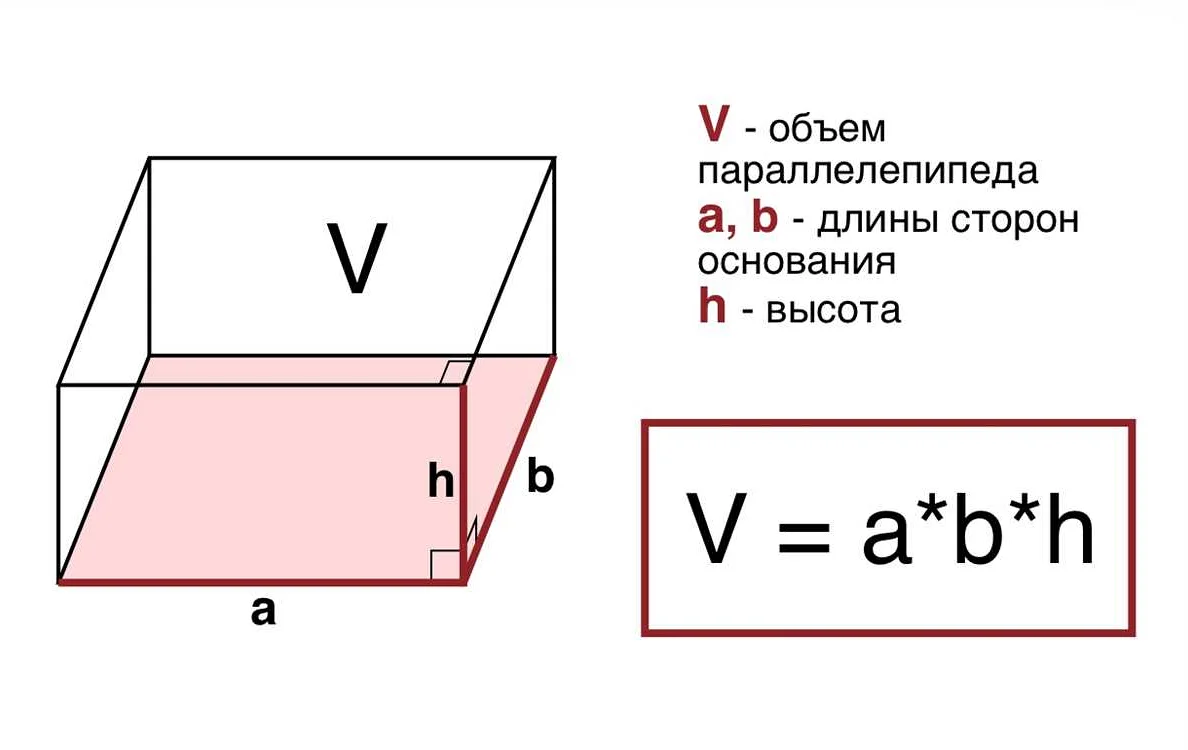
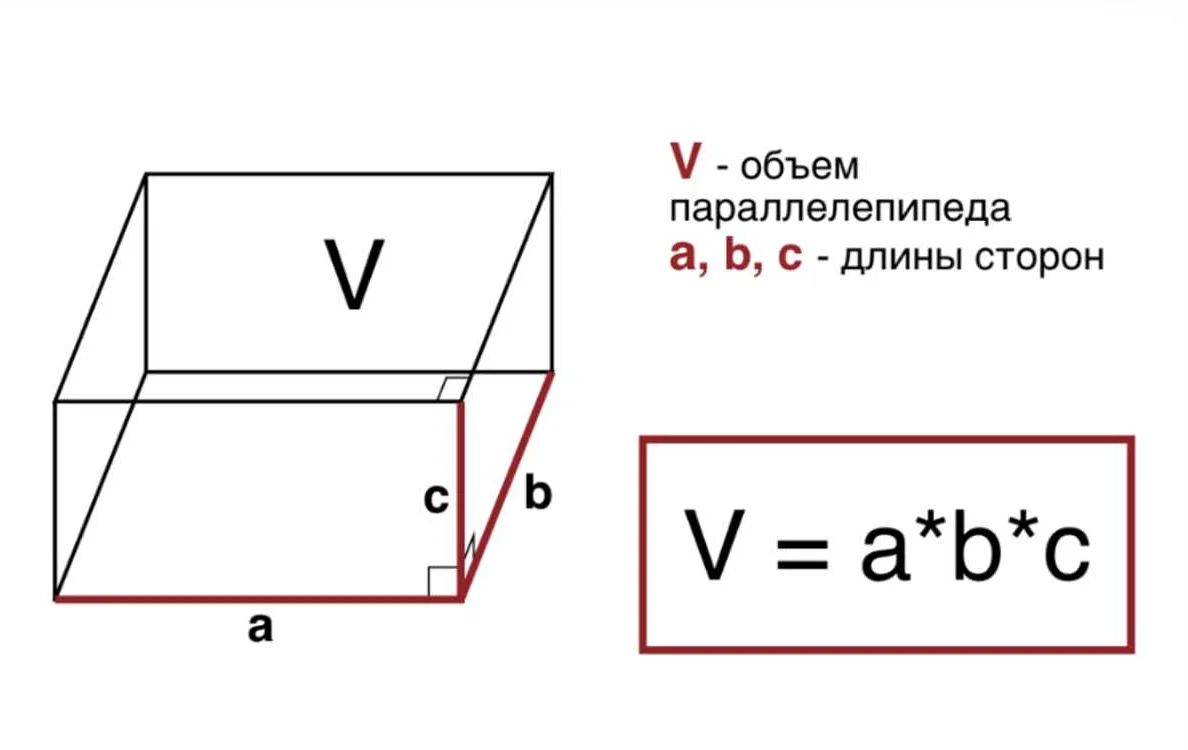
Для расчета объема различных геометрических тел, таких как параллелепипеды, цилиндры и пирамиды, используются специальные формулы, которые ученики изучают на уроках математики в 6 классе. Например, формула для расчета объема прямоугольного параллелепипеда выглядит так: V = a * b * h, где a, b и h – это соответственно длина, ширина и высота параллелепипеда.

Например, если у нас есть параллелепипед с длиной сторон 5 см, 8 см и 10 см, мы можем рассчитать его объем, умножив эти значения: V = 5 см * 8 см * 10 см = 400 см³.

Расчет объема позволяет ученикам лучше понять геометрические фигуры и их свойства, а также применять полученные знания в реальных ситуациях. Например, зная объем аквариума, можно рассчитать, сколько в него поместится воды или рыбок. Понимание объема также полезно в других науках, таких как физика, где объем используется для расчета плотности и других величин.

Объем в математике 6 класс: определение

Объем можно рассчитать для различных трехмерных фигур, таких как параллелепипеды, призмы, пирамиды и шары. Для каждой фигуры есть своя формула расчета объема.

Например, для параллелепипеда объем вычисляется по формуле: V = a * b * h, где a, b и h — длины сторон параллелепипеда.

Для призмы объем можно найти по формуле: V = S * h, где S — площадь основания призмы, а h — высота призмы.

Для пирамиды объем определяется по формуле: V = (S * h) / 3, где S — площадь основания пирамиды, а h — высота пирамиды.

И, наконец, для шара объем вычисляется по формуле: V = (4/3) * π * r³, где π — математическая константа, равная примерно 3,14, а r — радиус шара.

Расчеты объема помогают узнать, сколько пространства занимает та или иная фигура, что позволяет проводить различные практические задачи, например, планировать количество материала для изготовления предметов или определить объем жидкости в емкости.

Видео по теме:

Объем как величина в трехмерном пространстве

Для расчета объема трехмерных тел используются соответствующие формулы. Например, для прямоугольного параллелепипеда объем вычисляется по формуле:

объем = длина × ширина × высота

Другой пример – для цилиндра объем определяется по формуле:

объем = π × радиус² × высота

Знание понятия объема и умение его вычислять позволяет решать задачи, связанные с геометрией и практическими применениями. Например, зная объем прямоугольного параллелепипеда, можно вычислить, сколько в него войдет вещей или жидкости.

Способы измерения объема

Форма предметаСпособ измерения объема

Куб	Объем куба можно рассчитать, умножив длину его ребра на само себя три раза: V = a * a * a, где V – объем куба, а – длина ребра.
Параллелепипед	Объем параллелепипеда можно рассчитать, умножив длину, ширину и высоту: V = a * b * h, где V – объем параллелепипеда, a – длина, b – ширина, h – высота.
Цилиндр	Объем цилиндра можно рассчитать, умножив площадь основания на высоту: V = S * h, где V – объем цилиндра, S – площадь основания, h – высота.
Шар	Объем шара можно рассчитать по формуле: V = (4/3) * π * r^3, где V – объем шара, π – число пи (приближенно равно 3,14), r – радиус шара.

Измерение объема предметов является важной задачей как в математике, так и в реальной жизни. Знание способов измерения объема позволяет решать различные задачи, связанные с расчетами и конструированием.

Вопрос-ответ:

Что такое объем в математике?

Объем в математике — это величина, которая показывает, сколько пространства занимает тело. Он измеряется в кубических единицах (например, кубических сантиметрах или кубических метрах) и вычисляется путем умножения трех размеров тела: длины, ширины и высоты.

Для чего нужно знать объем тела?

Знание объема тела позволяет понять, сколько места займет это тело в пространстве. Например, зная объем комнаты, можно понять, сколько мебели в нее поместится. Знание объема также позволяет решать задачи по пересылке и хранению предметов.

Какой формулой вычисляется объем прямоугольного параллелепипеда?

Объем прямоугольного параллелепипеда вычисляется по формуле V = a * b * h, где V — объем, a — длина, b — ширина, h — высота параллелепипеда.

Можете привести пример вычисления объема прямоугольного параллелепипеда?

Конечно! Предположим, у нас есть прямоугольный параллелепипед с длиной 5 см, шириной 3 см и высотой 4 см. Чтобы найти объем этого параллелепипеда, нужно перемножить все три размера: 5 * 3 * 4 = 60 см³. Таким образом, объем этого параллелепипеда равен 60 кубическим сантиметрам.

Что делать, если у тела не прямоугольная форма?

Если у тела не прямоугольная форма, то для вычисления его объема нужно использовать специальные формулы, соответствующие его форме. Например, для вычисления объема цилиндра нужно использовать формулу V = πr²h, где V — объем, r — радиус основания цилиндра, h — высота цилиндра.

Что такое объем?

Объем — это физическая величина, которая показывает, сколько места занимает тело в трехмерном пространстве. В математике объем измеряется в кубических единицах (кубических метрах, кубических сантиметрах и т.д.).

Как считать объем фигуры?

Для расчета объема различных фигур существуют разные формулы. Например, для прямоугольного параллелепипеда объем вычисляется как произведение длины, ширины и высоты. Для сферы — это четыре трети радиуса в кубе, умноженные на число пи. Для цилиндра — это площадь основания, умноженная на высоту. В общем случае, для любой фигуры объем можно найти, если известны ее характеристики и применяются соответствующие формулы.

Примеры расчетов объема

Пример 1:

Рассмотрим прямоугольный параллелепипед со сторонами a = 4 см, b = 6 см и c = 3 см. Чтобы найти его объем, нужно умножить длины всех его сторон: V = a * b * c = 4 * 6 * 3 = 72 см³.

Пример 2:

Допустим, у нас есть цилиндр высотой h = 10 см и радиусом основания r = 5 см. Формула для расчета объема такого цилиндра выглядит так: V = π * r² * h, где π (пи) — это математическая константа, примерно равная 3.14159. Подставим значения: V = 3.14159 * 5² * 10 = 785.39815 см³ (округляется до 785.4 см³).

Пример 3:

Пусть у нас есть шар с радиусом r = 7 см. Формула для расчета объема шара выглядит так: V = (4/3) * π * r³. Подставим значение радиуса: V = (4/3) * 3.14159 * 7³ = 1436.75557 см³ (округляется до 1436.8 см³).

Пример 4:

Рассмотрим пирамиду с площадью основания S = 16 м² и высотой h = 5 м. Формула для расчета объема такой пирамиды выглядит так: V = (1/3) * S * h. Подставим значения: V = (1/3) * 16 * 5 = 26.66667 м³ (округляется до 26.7 м³).

Пример 5:

Представим, что у нас есть конус с радиусом основания r = 8 см и высотой h = 12 см. Формула для расчета объема такого конуса выглядит так: V = (1/3) * π * r² * h. Подставим значения: V = (1/3) * 3.14159 * 8² * 12 = 803.84 см³.

Расчет объема прямоугольного параллелепипеда

Формула для расчета объема прямоугольного параллелепипеда выглядит следующим образом:

V = a * b * h

где:

• V — объем прямоугольного параллелепипеда;
• a — длина прямоугольного параллелепипеда;
• b — ширина прямоугольного параллелепипеда;
• h — высота прямоугольного параллелепипеда.

Например, если длина параллелепипеда равна 4 см, ширина равна 3 см, а высота равна 2 см, то его объем можно рассчитать следующим образом:

V = 4 * 3 * 2 = 24 см³

Таким образом, объем прямоугольного параллелепипеда равен 24 кубическим сантиметрам.

Расчет объема цилиндра

Формула для расчета объема цилиндра выглядит следующим образом:

V = π * r^2 * h

Где:

• V – объем цилиндра
• π – математическая константа, приближенное значение которой равно 3,14
• r – радиус основания цилиндра
• h – высота цилиндра

Для примера, рассмотрим цилиндр с радиусом основания 2 см и высотой 5 см. Подставляя значения в формулу, получим:

V = 3,14 * 2^2 * 5 = 3,14 * 4 * 5 = 62,8 см^3

Таким образом, объем этого цилиндра равен 62,8 кубических сантиметра.

Расчет объема пирамиды

Объем пирамиды можно вычислить, зная площадь основания и высоту пирамиды. Формула для расчета объема пирамиды имеет вид:

V = (S * h) / 3

где V — объем пирамиды, S — площадь основания, h — высота пирамиды.

Пример 1:

• Площадь основания пирамиды равна 36 квадратных сантиметров.
• Высота пирамиды составляет 8 сантиметров.

Применяем формулу:

V = (36 * 8) / 3 = 96 / 3 = 32

Ответ: объем пирамиды равен 32 кубическим сантиметрам.

Пример 2:

• Площадь основания пирамиды равна 64 квадратных миллиметра.
• Высота пирамиды равна 5 миллиметров.

Применяем формулу:

V = (64 * 5) / 3 = 320 / 3 ≈ 106.67

Ответ: объем пирамиды приближенно равен 106.67 кубическим миллиметрам.

Таким образом, расчет объема пирамиды позволяет определить, сколько пространства занимает данная геометрическая фигура.

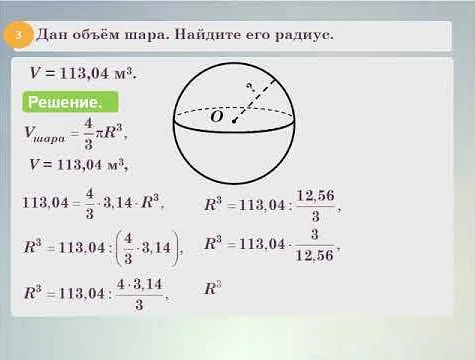
Расчет объема шара

V = (4/3) * π * r^3

где V обозначает объем шара, π (пи) — математическая константа, примерное значение которой равно 3,14, а r — радиус шара.

Пример расчета объема шара:

• У нас есть шар с радиусом 5 см.
• Подставляем значение радиуса в формулу: V = (4/3) * 3,14 * (5^3)
• Выполняем вычисления: V = (4/3) * 3,14 * 125
• Упрощаем выражение: V = 523,33 см³

Таким образом, объем шара с радиусом 5 см будет равен 523,33 см³.