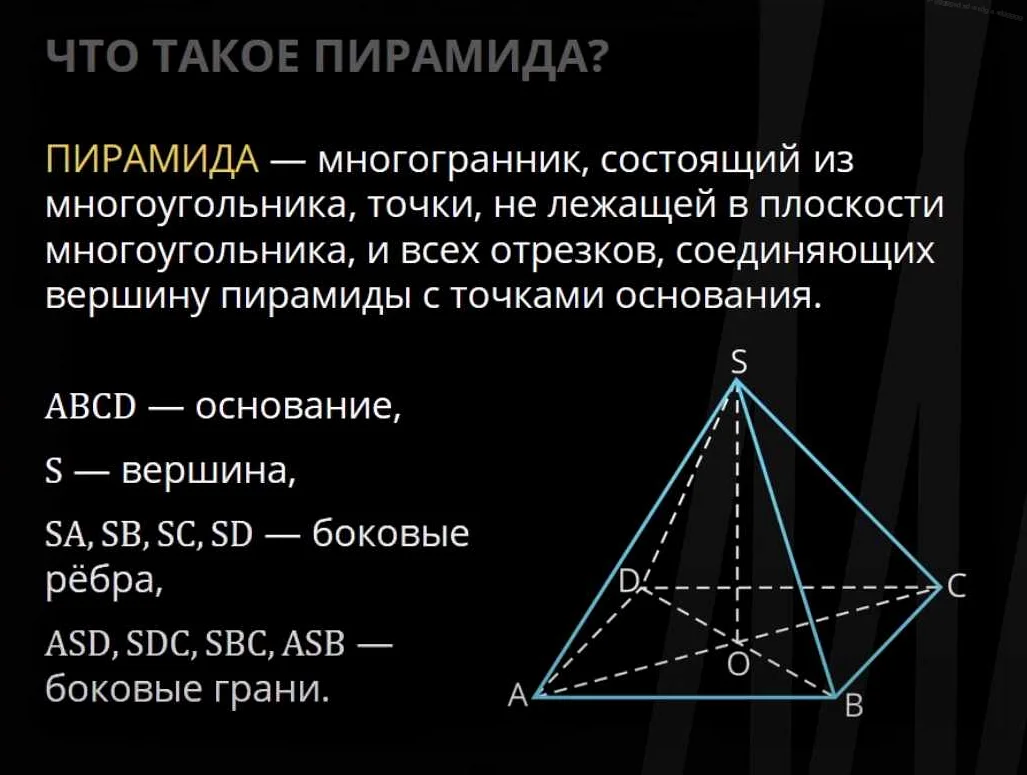
Что такое пирамида в математике

Пирамида в математике — это геометрическое тело, состоящее из многоугольного основания и треугольных граней, которые соединяются в вершине. Узнайте о свойствах и формулах для расчета объема и площади поверхности пирамиды.

Пирамида — это геометрическое тело, которое состоит из основания, которое может быть любой плоской фигурой, и трех или более треугольных граней, которые соединяются в одной точке, называемой вершиной пирамиды. Пирамиды являются важной частью изучения трехмерной геометрии и имеют много интересных свойств и характеристик.

Одно из основных свойств пирамиды — ее объем. Объем пирамиды можно найти, умножив площадь основания на высоту пирамиды и делением полученного значения на 3. Это математическое выражение для объема пирамиды обладает простотой и позволяет легко вычислить объем любой пирамиды при известных значениях.

Кроме объема, пирамиды также имеют другие свойства, такие как площадь поверхности, которая равна сумме площадей всех граней пирамиды, и высота пирамиды, которая проходит от вершины до основания перпендикулярно к основанию. Пирамиды могут быть различных форм и размеров, и их свойства могут варьироваться в зависимости от их конкретных характеристик.

Изучение пирамид в математике открывает большое количество интересных задач и применений. Пирамиды встречаются не только в геометрии, но и в других областях науки и техники. Они широко используются в архитектуре, физике, химии и даже в компьютерной графике. Понимание свойств и характеристик пирамид позволяет ученым и инженерам изучать различные системы и решать сложные задачи.

В заключение, пирамида — это геометрическое тело, которое имеет множество интересных свойств и характеристик. Изучение пирамиды в математике позволяет не только лучше понять трехмерную геометрию, но и применять этот знания для решения практических задач в различных областях науки и техники.

Определение пирамиды в математике

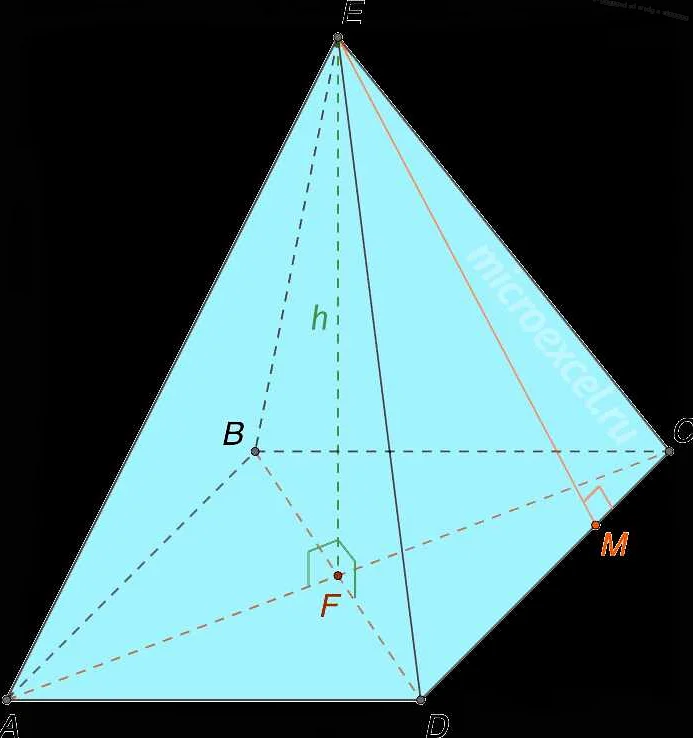
У пирамиды есть две особенности. Во-первых, она имеет одну и только одну вершину. Во-вторых, все боковые грани пирамиды являются треугольниками. Основание пирамиды может быть различной формы: треугольником, квадратом, прямоугольником и т. д. Важно отметить, что у пирамиды может быть различное число граней, включая основание и боковые грани.

Пирамиды в математике широко используются для решения различных задач и моделирования реальных объектов. Они играют важную роль в геометрии, а также находят применение в физике, химии, архитектуре и других науках.

Видео по теме:

Геометрические свойства пирамиды

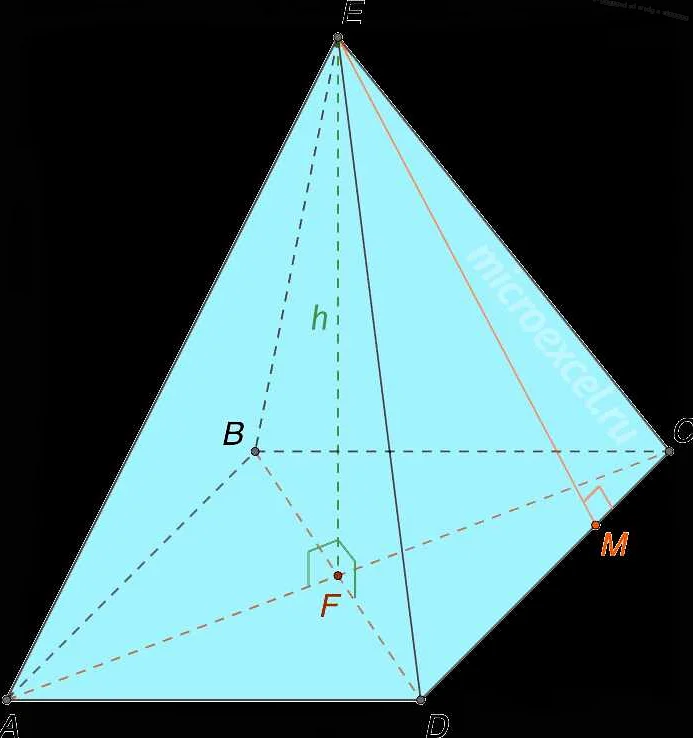
Одно из главных геометрических свойств пирамиды — ее высота. Высота пирамиды — это расстояние от вершины до плоскости, на которой лежит основание. Другими словами, это перпендикуляр, опущенный из вершины на плоскость основания.

Важное свойство пирамиды — ее объем. Объем пирамиды можно вычислить по формуле: V = (1/3) * S * h, где S — площадь основания пирамиды, а h — ее высота. Также пирамиду можно разделить на пирамиды меньших размеров, сохраняя при этом пропорции площадей оснований и высот.

Еще одно интересное свойство пирамиды — ее боковая площадь. Боковая площадь пирамиды — это сумма площадей ее боковых граней. Для пирамиды с регулярным основанием (т.е. основание является правильным многоугольником), боковая площадь можно вычислить по формуле: Sб = (Pб * l) / 2, где Pб — периметр основания пирамиды, а l — длина бокового ребра пирамиды.

Пирамиды также имеют свойство симметрии. Если плоскость разделяет пирамиду пополам так, что она проходит через вершину и середину ребра основания, то две полученные части пирамиды будут подобными и равными по объему.

Объем и площадь поверхности пирамиды

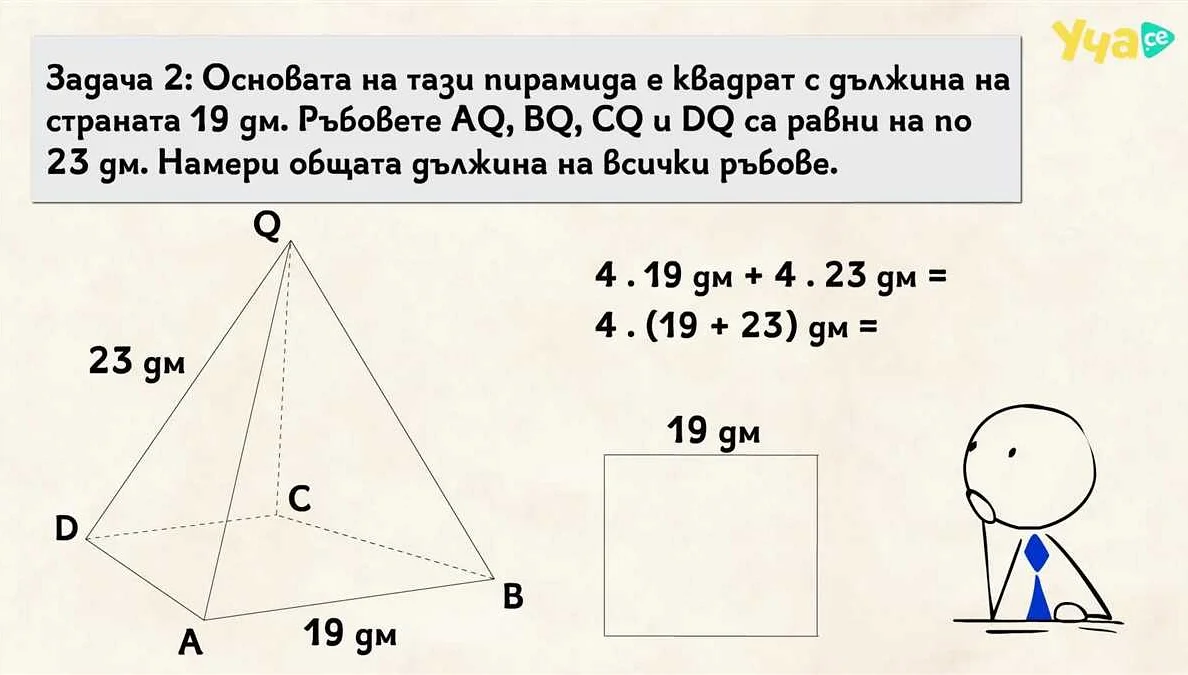
Для правильной пирамиды (когда основание является правильным многоугольником и все боковые грани равны) объем можно вычислить по формуле:

Формула для объема:

V = (S * h) / 3

где V — объем пирамиды, S — площадь основания, h — высота пирамиды.

Площадь поверхности пирамиды складывается из площади основания и площади боковых граней. Для правильной пирамиды площадь поверхности можно вычислить по формуле:

Формула для площади поверхности:

Sпов = Sосн + Sбок

где Sпов — площадь поверхности пирамиды, Sосн — площадь основания, Sбок — площадь боковых граней.

Для пирамиды с произвольным основанием и высотой сложнее вывести общую формулу, поэтому в таких случаях приходится использовать геометрические методы или разбивать пирамиду на более простые фигуры, для которых известны формулы вычисления объема и площади поверхности.

Вопрос-ответ:

Что такое пирамида в математике?

В математике пирамида — это трехмерная геометрическая фигура, у которой основание является многоугольником, а все остальные боковые грани являются треугольниками, сходящимися к одной вершине.

Какие свойства имеет пирамида в математике?

У пирамиды есть несколько свойств. Одно из них — высота пирамиды, которая является перпендикуляром, опущенным из вершины пирамиды на плоскость основания. Еще одно свойство — объем пирамиды, который можно вычислить по формуле: V = (1/3) * S * h, где S — площадь основания, а h — высота пирамиды.

Как можно классифицировать пирамиды в математике?

Пирамиды можно классифицировать по форме основания. Если основание пирамиды — правильный многоугольник и все боковые грани равнобедренные треугольники, то такая пирамида называется правильной. В противном случае пирамида называется неправильной.

Какие еще формулы связаны с пирамидой в математике?

Помимо формулы для вычисления объема пирамиды, есть и другие формулы связанные с пирамидой. Например, формула для вычисления площади боковой поверхности пирамиды: Sбок = (1/2) * p * l, где p — периметр основания, l — образующая пирамиды. Также есть формула для вычисления площади основания пирамиды: Sосн = (1/4) * n * a2 * cot(180/n), где n — количество сторон многоугольника основания, a — длина стороны многоугольника.

Какие еще интересные свойства пирамиды в математике?

Пирамида обладает несколькими интересными свойствами. Например, все боковые ребра пирамиды имеют одинаковую длину. Также, сумма длин всех ребер пирамиды равна удвоенной сумме длин ребер основания. Кроме того, пирамида может быть сечена плоскостью, проходящей через вершину и параллельной плоскости основания, таким образом получается плоское сечение пирамиды, которое может быть различной формы.

Различные типы пирамид в математике

В математике существует несколько различных типов пирамид, которые отличаются формой и структурой.

1. Треугольная пирамида: эта пирамида имеет треугольное основание и треугольные боковые грани.

2. Квадратная пирамида: основание этой пирамиды является квадратом, а боковые грани также являются квадратами.

3. Правильная пирамида: основание и боковые грани этой пирамиды являются правильными многоугольниками одинаковой формы.

4. Неправильная пирамида: в отличие от правильной пирамиды, у неправильной пирамиды основание и боковые грани имеют различные формы.

5. Усеченная пирамида: это пирамида, у которой верхняя часть отсечена плоскостью, параллельной основанию.

6. Ромбическая пирамида: основание этой пирамиды является ромбом, а боковые грани имеют форму треугольников.

Это лишь некоторые примеры типов пирамид, которые могут встречаться в математике. Каждый тип пирамиды имеет свои особенности и свойства, которые могут быть изучены и применены при решении различных задач и заданий.

Связь пирамиды с другими геометрическими фигурами

Например, пирамида похожа на конус. Обе фигуры имеют одну вершину и плоское основание, но у пирамиды основание может быть любой плоской фигурой, в то время как у конуса основание всегда является кругом.

Также пирамида может быть похожа на призму, но у призмы все ребра параллельны и равны между собой, в то время как у пирамиды ребра могут быть разной длины и не параллельны друг другу.

Пирамида также может быть связана с параллелепипедом. Если основание пирамиды является прямоугольником, то она становится похожей на параллелепипед. Однако, у пирамиды только одно основание, в то время как параллелепипед имеет два противоположных параллелограмма.

Таким образом, пирамида имеет свои особенности, но также имеет общие черты с другими геометрическими фигурами, что делает ее интересной и важной для изучения в математике.

Пирамиды в природе и архитектуре

Самыми известными пирамидами являются египетские пирамиды. Они построены из каменных блоков и служили гробницами фараонов. Самая известная из них – пирамида Хеопса, которая была построена около 4500 лет назад и является одним из Семи чудес света древности.

Кроме Египта, пирамиды можно найти и в других странах. Например, в Мексике расположена пирамида Хеопса, которая является одним из главных археологических объектов Юкатана. В Мексике также находится пирамида Кукулькана, которая известна своей геометрической точностью и своими астрономическими особенностями.

Пирамиды можно найти также в Центральной Америке, например, в Гватемале, Гондурасе и Сальвадоре. Там они были построены майями и ацтеками и служили религиозным и культурным центрам.

В природе также можно обнаружить пирамиды. Например, в Алжире находятся пирамиды Ахмеда, которые представляют собой выступающие пики в пустыне. Они образовались из-за эрозии и представляют собой уникальный природный феномен.

Таким образом, пирамиды – это не только математические структуры, но и удивительные архитектурные сооружения и природные объекты, которые имеют большую историческую и культурную ценность.

Пирамиды в математических расчетах

Пирамиды имеют несколько свойств, которые позволяют проводить различные математические операции с этими телами. Одно из основных свойств пирамиды — равенство площадей основания и боковых граней. Это означает, что площадь каждой боковой грани равна площади основания пирамиды.

Кроме того, пирамиды имеют высоту, которая является перпендикулярным расстоянием от вершины пирамиды до плоскости основания. Высота пирамиды может быть использована для вычисления объема пирамиды, который равен одной трети произведения площади основания на высоту.

Пирамиды также могут быть классифицированы по форме и количеству граней. Например, треугольная пирамида имеет треугольное основание и четыре треугольные грани, в то время как четырехугольная пирамида имеет четырехугольное основание и пять граней.

В заключение, пирамиды являются важным инструментом в математических расчетах и позволяют решать разнообразные задачи, связанные с пространственными структурами и объемами.

Применение пирамид в реальной жизни

Одним из наиболее ярких примеров применения пирамид является архитектура. Многие знаменитые сооружения, такие как пирамиды Гизы в Египте или Лувр в Париже, имеют форму пирамиды. Эта форма позволяет создать прочное и устойчивое строение, которое может выдерживать большие нагрузки.

Пирамиды также применяются в математике и физике. Например, пирамиды используются для решения различных задач, связанных с объемом и площадью фигур. Они также могут быть использованы для моделирования реальных объектов и явлений.

Еще одним примером применения пирамид является маркетинг и управление бизнесом. Концепция пирамидальной структуры используется в многоуровневом маркетинге, где каждый уровень представляет собой пирамиду с определенным количеством продавцов. Это позволяет организации эффективно управлять своими продажами и расширять свою сеть.

Таким образом, пирамиды имеют широкое применение в реальной жизни и являются важной частью различных областей, таких как архитектура, математика, физика и бизнес.