Произведение это что в математике определение

Произведение в математике — это операция, которая обозначает умножение двух или более чисел. В данной статье вы узнаете, как определяется произведение и какие основные свойства оно обладает.

Произведение — одна из основных операций в математике, которая позволяет узнать результат умножения двух или более чисел. В математической записи произведение обозначается знаком умножения «×» или точкой «.». Например, произведение чисел 5 и 3 обозначается как 5 × 3 или 5 · 3.

Произведение может быть найдено путем повторения сложения одного числа столько раз, сколько указано вторым числом. Например, произведение 5 × 3 можно найти, складывая число 5 три раза: 5 + 5 + 5 = 15. Таким образом, произведение 5 × 3 равно 15.

Произведение может также быть найдено путем группировки и суммирования чисел. Например, произведение 2 × 4 можно найти, сгруппировав числа следующим образом: (2 + 2) + (2 + 2) = 8. Таким образом, произведение 2 × 4 равно 8.

Произведение имеет несколько свойств, которые позволяют упростить его вычисление. Например, произведение любого числа на 1 равно этому числу: а × 1 = а. Также произведение числа на 0 всегда равно 0: а × 0 = 0. Эти свойства помогают сократить процесс вычисления произведения и упростить математические операции.

Понятие произведения

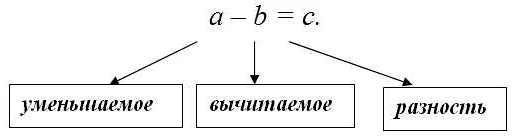
Произведение обозначается знаком умножения (×) или точкой (·) между множителями. Например, произведение двух чисел a и b может быть записано как a × b или a · b.

Произведение может быть вычислено для любых чисел, включая целые числа, дроби и действительные числа. Например, произведение чисел 2 и 3 равно 6, так как 2 × 3 = 6.

Произведение также имеет ряд свойств, таких как коммутативность (меняется порядок множителей не влияет на результат) и ассоциативность (меняется порядок выполнения операций не влияет на результат).

Примеры произведений:

Произведение чисел 4 и 5 равно 20, так как 4 × 5 = 20.

Произведение чисел 0 и 7 равно 0, так как 0 × 7 = 0.

Произведение чисел 1 и 10 равно 10, так как 1 × 10 = 10.

Произведение чисел -2 и -3 равно 6, так как -2 × -3 = 6.

Произведение числа 5 и 1/2 равно 2.5, так как 5 × 1/2 = 2.5.

Произведение двух переменных a и b в математике может быть записано как a × b или ab и может быть использовано для решения различных математических задач.

Видео по теме:

Определение произведения

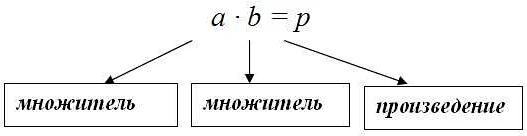
В математике произведением двух чисел называется результат их умножения. Произведение обозначается знаком умножения «×» или точкой «.».

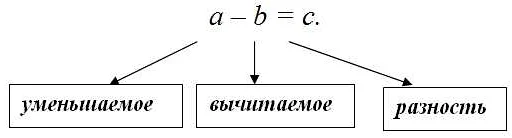
Пусть у нас есть два числа a и b. Тогда их произведение будет равно c:

a

×

b

=

c

Например, произведение чисел 3 и 4 будет:

3

×

4

=

12

Таким образом, произведение чисел 3 и 4 равно 12.

Важно отметить, что произведение чисел не зависит от их порядка. То есть, произведение чисел a и b всегда будет равно произведению чисел b и a:

a	×	b	=	c
b	×	a	=	c

Например, произведение чисел 3 и 4 равно произведению чисел 4 и 3:

3	×	4	=	12
4	×	3	=	12

Таким образом, произведение чисел 3 и 4 равно 12, а произведение чисел 4 и 3 также равно 12.

Примеры произведения

Вот несколько примеров произведения:

1. Произведение чисел 2 и 3 равно 6. Это можно записать как 2 × 3 = 6.
2. Произведение чисел 5 и 7 равно 35. Это можно записать как 5 × 7 = 35.
3. Произведение чисел 10 и -2 равно -20. Это можно записать как 10 × -2 = -20.

Как видно из примеров, произведение чисел может быть как положительным, так и отрицательным числом. Также важно помнить, что произведение любого числа на ноль равно нулю.

Как вычислить произведение чисел

Для вычисления произведения чисел, нужно умножить все числа между собой. Например, чтобы найти произведение чисел 3, 4 и 5, нужно умножить 3 на 4, а затем умножить результат на 5:

3 × 4 × 5 = 60

Таким образом, произведение чисел 3, 4 и 5 равно 60.

Вычисление произведения чисел может быть осуществлено с помощью калькулятора или математического программного обеспечения. В случае большого количества чисел, удобно использовать математические формулы или алгоритмы для автоматизации процесса вычисления.

Произведение чисел может быть положительным, отрицательным или равным нулю в зависимости от значений чисел, участвующих в умножении.

Например:

-3 × 4 = -12 (произведение двух чисел с разными знаками будет отрицательным)

0 × 6 = 0 (произведение любого числа на ноль будет равно нулю)

Таким образом, вычисление произведения чисел является простой, но важной операцией в математике, которая позволяет получить новое число путем умножения двух или более чисел.

Важные свойства произведения

В математике произведение обладает несколькими важными свойствами, которые помогают в решении различных задач и упрощают вычисления. Рассмотрим некоторые из них:

СвойствоОписание

Коммутативность	Произведение двух чисел не зависит от порядка, в котором они умножаются. То есть для любых чисел a и b выполняется равенство a * b = b * a.
Ассоциативность	Произведение трех и более чисел можно выполнять в любом порядке, результат будет одинаковым. То есть для любых чисел a, b и c выполняется равенство (a * b) * c = a * (b * c).
Дистрибутивность	Произведение числа a на сумму чисел b и c равно сумме произведений a на b и a на c. То есть для любых чисел a, b и c выполняется равенство a * (b + c) = a * b + a * c.
Единица	Произведение числа a на 1 равно самому числу a. То есть для любого числа a выполняется равенство a * 1 = a.
Ноль	Произведение числа a на 0 равно 0. То есть для любого числа a выполняется равенство a * 0 = 0.

Эти свойства произведения являются основой для многих математических доказательств и применяются в различных областях, таких как алгебра, геометрия, физика и экономика.

Произведение в различных областях математики

Анализ: В математическом анализе произведение — это операция, обратная делению. Если одно число является делителем другого числа, то их произведение равно делимому. Например, если 2 является делителем числа 6, то их произведение равно 6.

Теория вероятностей: В теории вероятностей произведение двух вероятностей — это вероятность того, что оба события произойдут. Например, если вероятность выпадения головы при подбрасывании монеты равна 0.5, а вероятность выпадения орла равна 0.3, то вероятность выпадения и головы, и орла равна 0.15.

Линейная алгебра: В линейной алгебре произведение матриц — это операция, которая соответствует композиции линейных преобразований. Например, если у нас есть матрица A и матрица B, то их произведение AB будет новой матрицей, полученной путем умножения строк матрицы A на столбцы матрицы B.

Дискретная математика: В дискретной математике произведение — это операция, которая определена на множествах. Например, произведение двух множеств A и B состоит из всех возможных пар (a, b), где a принадлежит множеству A, а b принадлежит множеству B.

Топология: В топологии произведение — это понятие, которое определяется на произвольных топологических пространствах. Например, произведение двух топологических пространств A и B — это новое топологическое пространство, состоящее из всех возможных упорядоченных пар (a, b), где a принадлежит пространству A, а b принадлежит пространству B.

Таким образом, понятие произведения используется в различных областях математики и имеет различные значения в каждой из них.

Произведение в алгебре и геометрии

В алгебре произведение определено для чисел и других алгебраических объектов, таких как векторы, матрицы и многочлены. В случае чисел, произведение двух чисел a и b обозначается как a * b или ab и является результатом умножения этих чисел. Например, произведение 3 и 4 равно 12 (3 * 4 = 12). В случае векторов и матриц, произведение определяется посредством соответствующих операций умножения векторов и матриц.

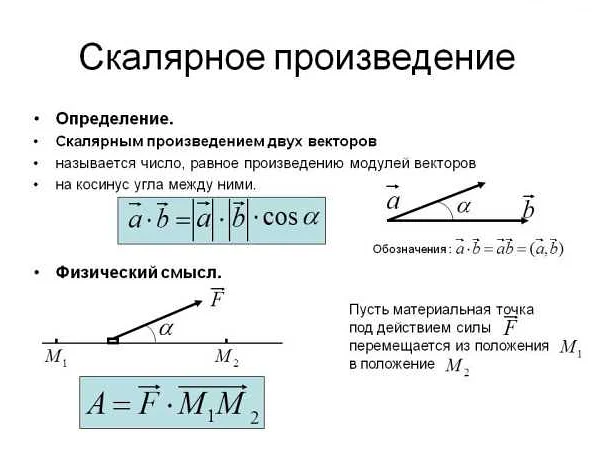
В геометрии произведение может иметь другую интерпретацию. Например, векторное произведение двух векторов задает новый вектор, перпендикулярный плоскости, образованной исходными векторами. Это понятие широко используется в физике и инженерии для моделирования трехмерных пространственных векторов и вращений.

Также в геометрии произведение может быть определено для других геометрических объектов, например, для площадей и объемов. Например, площадь прямоугольника вычисляется как произведение его длины и ширины, а объем параллелепипеда – как произведение его трех размеров: длины, ширины и высоты.

Таким образом, произведение в алгебре и геометрии является важной математической операцией, которая имеет различные значения и интерпретации в зависимости от контекста. Оно позволяет умножать числа, векторы, матрицы и другие алгебраические и геометрические объекты, что является фундаментальным для многих областей математики и ее приложений.

Вопрос-ответ:

Что такое произведение в математике?

Произведение в математике — это операция умножения двух или более чисел, которая позволяет найти результат умножения.

Как определить произведение чисел?

Для определения произведения чисел нужно умножить эти числа друг на друга. Например, произведение чисел 2 и 3 равно 6 (2 * 3 = 6).

Какое свойство имеет произведение чисел?

Произведение чисел обладает свойствами коммутативности и ассоциативности. Свойство коммутативности означает, что порядок множителей не влияет на результат умножения. Свойство ассоциативности позволяет менять порядок скобок при умножении нескольких чисел.

Какие примеры произведений чисел можно привести?

Примеры произведений чисел: 2 * 3 = 6, 5 * 4 = 20, 7 * 9 = 63. В этих примерах первое число является множителем, второе число — также множителем, а результат умножения — произведением.

Как можно записать произведение чисел в математике?

Произведение чисел в математике обычно записывается с помощью знака умножения (*). Например, 3 * 4 = 12. Также произведение можно записать с помощью точки (·) или отсутствующего знака. Кроме того, в математике используется обозначение «×» для произведения чисел.

Что такое произведение в математике?

Произведение в математике — это операция умножения двух или более чисел, которая позволяет найти результат их умножения. В математических выражениях произведение обозначается знаком умножения «*», а числа, участвующие в умножении, называются множителями. Результат умножения называется произведением.

Как найти произведение двух чисел?

Для того, чтобы найти произведение двух чисел, необходимо умножить эти числа между собой. Например, чтобы найти произведение чисел 4 и 7, нужно умножить 4 на 7, получив результат 28. Таким образом, произведение чисел 4 и 7 равно 28.