Что такое плюс в математике определение
Содержимое
- 1 Что такое плюс в математике определение
- 1.1 Определение плюса в математике
- 1.2 Примеры использования плюса в математике
- 1.3 Свойства плюса в математике
- 1.4 Значение плюса в арифметике
- 1.5 Плюс в алгебре: основные правила
- 1.6 Плюс в геометрии: применение
- 1.7 Плюс в статистике и вероятности
- 1.8 Плюс в компьютерной науке и программировании
- 1.9 Вопрос-ответ:
- 1.10 Видео по теме:
Плюс в математике — это знак, обозначающий операцию сложения. Он используется для объединения чисел или выражений и находится между ними. Плюс применяется для увеличения значения одного числа на другое или для объединения двух чисел в сумму. Определение плюса в математике является основой для изучения арифметических операций и образует базу для дальнейших математических концепций и применений.
Плюс — это одна из основных операций в математике, которую мы используем в повседневной жизни. Она обозначается знаком «+» и выполняется для сложения двух или более чисел. Сложение позволяет объединить эти числа и получить их сумму.
Знак плюс имеет несколько свойств. Во-первых, сложение коммутативно, то есть порядок слагаемых не имеет значения. Например, 2 + 3 равно 3 + 2. Во-вторых, сложение ассоциативно, что означает, что можно складывать числа по частям. Например, (2 + 3) + 4 равно 2 + (3 + 4).
Примеры сложения помогут лучше понять плюс в математике. Например, 2 + 3 равно 5, 8 + 6 равно 14, а 10 + 10 равно 20. Сложение можно применять не только к целым числам, но и к десятичным дробям (например, 1.5 + 2.3 равно 3.8) и отрицательным числам (например, -3 + -7 равно -10).
В математике плюс используется не только для сложения чисел, но и для других операций, таких как сложение векторов или сложение многочленов. Знание плюса и его свойств позволяет нам лучше понять и решать различные математические задачи.
Определение плюса в математике
- Порядок слагаемых не влияет на результат: a + b = b + a
- При сложении двух чисел получается третье число, которое называется суммой.
- Сложение можно продолжать и на большее количество чисел: a + b + c + …
- Плюс является операцией коммутативной: a + b = b + a
- Плюс является операцией ассоциативной: (a + b) + c = a + (b + c)
Например, при сложении чисел 2 и 3 получается сумма 5: 2 + 3 = 5. Также можно сложить несколько чисел, например, 2 + 3 + 4 = 9. Плюс широко используется в арифметике, алгебре и других областях математики.
Примеры использования плюса в математике

1. Сложение чисел:
Например, 2 + 3 = 5. В этом примере плюс используется для сложения числа 2 и числа 3, что дает результат 5.
2. Сложение переменных:
Плюс также может использоваться для сложения переменных. Например, если у нас есть переменная «а» со значением 4 и переменная «b» со значением 6, то «a + b» будет равно 10.
3. Сложение выражений:
Плюс можно использовать для сложения выражений. Например, если у нас есть выражение «2x + 3y», где «x» и «y» — переменные, то это означает, что мы складываем два различных слагаемых: «2x» и «3y».
4. Использование плюса в формулах:
Плюс может использоваться в математических формулах для обозначения сложения различных величин или переменных. Например, в формуле «F = ma», где «F» — сила, «m» — масса и «a» — ускорение, плюс используется для обозначения сложения массы и ускорения для расчета силы.
5. Использование плюса в алгебре:
Плюс является одной из основных операций в алгебре и используется для сложения различных алгебраических выражений. Например, в выражении «2x + 3y + 4z», плюс используется для сложения трех слагаемых «2x», «3y» и «4z».
Таким образом, плюс является важным математическим символом, который используется для сложения чисел, переменных, выражений и в формулах. Он позволяет объединять различные значения и получать их сумму.
Свойства плюса в математике
2. Ассоциативность: Плюс является ассоциативной операцией, то есть результат сложения трех чисел не зависит от того, какие из них будут складываться первыми. Например, для любых трех чисел a, b и c выполняется равенство (a + b) + c = a + (b + c).
3. Нейтральный элемент: Число 0 является нейтральным элементом относительно сложения. Это означает, что при сложении любого числа с нулем, результат будет равен этому числу. Например, для любого числа a выполняется равенство a + 0 = a.
4. Обратный элемент: Для каждого числа a существует обратное число (-a), такое что a + (-a) = 0. Обратное число отрицает значение данного числа. Например, для любого числа a выполняется равенство a + (-a) = 0.
5. Замкнутость: Множество всех целых чисел является замкнутым относительно сложения. Это означает, что если сложить два целых числа, то результат также будет целым числом.
6. Свойство треугольника: Для любых трех чисел a, b и c справедливо неравенство a + b > c. Это свойство позволяет определить, можно ли построить треугольник с заданными сторонами.
7. Свойство транзитивности: Если a > b и b > c, то a > c. То есть, если одно число больше второго, а второе число больше третьего, то первое число также больше третьего.
8. Свойство сравнения: Если a > b и c > d, то a + c > b + d. То есть, если одна сумма больше другой, то их сумма также больше.
Значение плюса в арифметике
Пример:
ВыражениеРезультат
| 2 + 3 | 5 |
| 10 + (-5) | 5 |
| -2 + (-3) | -5 |
Свойства плюса:
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существует нейтральный элемент относительно сложения — ноль: a + 0 = a
- Существует обратный элемент относительно сложения — противоположное число: a + (-a) = 0
Использование плюса в арифметике позволяет совершать сложение чисел и выполнять различные математические операции.
Плюс в алгебре: основные правила

Основные правила сложения с помощью плюса в алгебре:
- Коммутативность: порядок слагаемых не влияет на результат. Например, a + b = b + a.
- Ассоциативность: скобки можно расставлять по своему усмотрению. Например, (a + b) + c = a + (b + c).
- Существование нуля: любое число плюс ноль равно этому числу. Например, a + 0 = a.
- Обратное число: для любого числа a существует такое число -a, что a + (-a) = 0.
Помимо этих основных правил, плюс в алгебре обладает еще несколькими свойствами:
- Перестановка слагаемых: можно менять местами слагаемые без изменения результата. Например, (a + b) + c = (c + b) + a.
- Сокращение слагаемых: если два слагаемых равны по значению, их можно заменить на одно слагаемое с удвоенным коэффициентом. Например, a + a = 2a.
Знание основных правил плюса в алгебре позволяет упростить сложные выражения и решать уравнения.
Плюс в геометрии: применение
Плюс, как математический символ, имеет широкое применение не только в арифметике, но и в геометрии. В геометрии плюс может обозначать несколько различных вещей в зависимости от контекста.
Одним из основных применений плюса в геометрии является обозначение пересечения прямых или отрезков. Если две прямые пересекаются в одной точке, то в этой точке можно нарисовать плюс. Аналогично, если отрезки пересекаются, то в точке пересечения можно нарисовать плюс.
Еще одним применением плюса в геометрии является обозначение угловой меры. Если угол имеет меру, равную нулю или положительному числу, то его можно обозначить плюсом. Например, угол в 45 градусов можно обозначить как 45°+.
Также плюс используется для обозначения суммы двух векторов. Если имеются два вектора, то их сумма может быть обозначена как V1 + V2, где V1 и V2 — векторы.
Плюс в геометрии также может использоваться для обозначения суммы площадей. Например, если имеются две фигуры с площадями S1 и S2, то их суммарная площадь может быть обозначена как S1 + S2.
Таким образом, плюс в геометрии имеет несколько различных применений, связанных с пересечением прямых и отрезков, угловой мерой, суммой векторов и суммой площадей.
Плюс в статистике и вероятности

В статистике и вероятности знак «плюс» может иметь несколько значений и использоваться в различных контекстах.
Одно из распространенных применений плюса в статистике — это обозначение положительного значения. Например, если мы говорим о прибыли компании, то плюс перед числом указывает на то, что прибыль положительна.
Вероятность также может быть обозначена с помощью плюса. Если вероятность события равна 0.8, то ее можно записать как 0.8+ или 0.8*100%.
Еще одно важное применение плюса в статистике — это обозначение увеличения или прироста. Например, если мы говорим о приросте населения, то плюс перед числом указывает на увеличение числа людей.
Также в статистике и вероятности плюс может использоваться для обозначения добавочной информации или дополнительных условий. Например, если мы говорим о среднем значении, то плюс может указывать на добавочную информацию, например, «среднее значение + стандартное отклонение».
Плюс в статистике и вероятности может иметь различные значения и использоваться в разных контекстах. Он является важным инструментом для обозначения положительных значений, вероятностей, прироста и дополнительной информации.
Плюс в компьютерной науке и программировании
Операция сложения является одной из основных арифметических операций и используется для суммирования двух или более чисел. Например, выражение «2 + 3» вернет результат 5.
Помимо сложения чисел, символ «плюс» также может использоваться для объединения строк или конкатенации. Например, строка «Hello» + «World» вернет результат «HelloWorld».
В некоторых языках программирования, таких как JavaScript, оператор «+» также может использоваться для конкатенации строк с числами. Например, выражение «2 + 3 + ‘ apples'» вернет результат «5 apples».
Кроме того, символ «плюс» может использоваться для выполнения других операций, таких как инкремент и декремент. Например, выражение «x++» увеличит значение переменной x на 1, а выражение «x—» уменьшит значение переменной x на 1.
Также символ «плюс» может использоваться для выполнения операции сложения в контексте массивов или списков. Например, выражение [1, 2, 3] + [4, 5, 6] вернет результат [1, 2, 3, 4, 5, 6].
В программировании символ «плюс» имеет свои особенности и правила использования в различных языках программирования. Поэтому при разработке программ всегда необходимо учитывать специфику конкретного языка и правильно использовать оператор «+» в соответствии с его правилами.
Вопрос-ответ:
Зачем нужен плюс в математике?
Плюс в математике используется для обозначения операции сложения, то есть объединения двух чисел в одно число.
Можно ли использовать плюс в других операциях, кроме сложения?
В математике плюс используется только для обозначения операции сложения. Для других операций, таких как вычитание, умножение и деление, используются соответствующие знаки и символы.
Как записывается операция сложения с помощью плюса?
Операция сложения записывается с помощью плюса следующим образом: a + b = c, где a и b — слагаемые, а c — сумма.
Можно ли сложить число с самим собой?
Да, можно сложить число с самим собой. Например, 2 + 2 = 4.

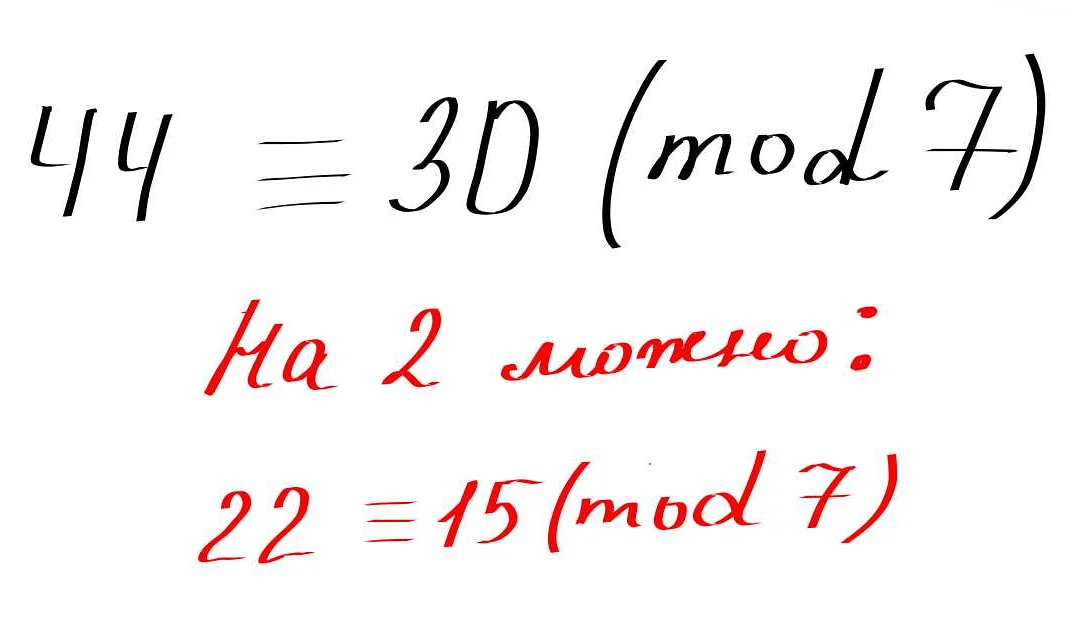

Статья очень понятно и доступно объясняет, что такое плюс в математике. Мне нравится, как автор подходит к описанию данного понятия. Он объясняет, что знак плюс используется для сложения чисел, а также демонстрирует его в примерах. Мне понравилось, что автор также рассказывает о свойствах плюса, например, коммутативности и ассоциативности. Это помогает лучше понять, как работает этот знак. Теперь я знаю, что плюс – это не просто знак, а математическая операция, которая позволяет складывать числа. Статья очень полезна и понятна, она помогла мне освежить свои знания в математике. Спасибо автору за такое информативное объяснение!