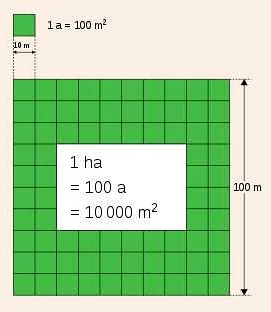
Что такое площадь 2 класс математика

Что такое площадь во втором классе математики? Узнайте, как дети учатся измерять площадь объектов, используя простые методы и понятия во время уроков математики в начальной школе.

Площадь — это мера пространства, занимаемого поверхностью или фигурой на плоскости. Размер площади измеряется в квадратных единицах, таких как квадратные сантиметры (см²) или квадратные метры (м²).

Понятие площади является одним из основных в математике и широко используется в жизни и научных исследованиях. Площадь позволяет определить, сколько пространства занимает конкретная фигура или поверхность, что позволяет нам производить расчеты и сравнения.

Например, с помощью площади можно определить, какой ковер нужно выбрать для покрытия пола в комнате, или сколько земли нужно для выращивания определенного количества растений.

Для вычисления площади различных фигур используются разные формулы. Каждая фигура имеет свою особенность, и для нее может быть найдена соответствующая формула вычисления площади.

Определение понятия «площадь»

Для нахождения площади различных фигур используются разные формулы. Например, для прямоугольника площадь равна произведению длины одной стороны на длину другой стороны. Для квадрата площадь равна квадрату длины его стороны.

Также площадь может быть определена с помощью геометрической модели. Например, площадь прямоугольника можно найти, разбив его на равные квадраты и посчитав количество этих квадратов. А площадь треугольника можно найти, разбив его на половинки и посчитав площади этих половинок.

Понятие площади имеет важное значение в математике и других науках, таких как геометрия, физика и строительство. Оно позволяет решать задачи связанные с измерением и оценкой площади поверхностей, проводить сравнения и анализ различных фигур по их площади.

Видео по теме:

Как измеряется площадь

Для измерения площади различных фигур используются разные формулы. Например, для прямоугольника площадь равна произведению длины одной стороны на длину другой стороны. Для квадрата площадь равна квадрату длины одной из его сторон.

Чтобы измерить площадь фигуры, можно воспользоваться геометрической сеткой или раскрасить фигуру квадратами единичной площади и посчитать их количество.

Зная площадь фигуры, можно сравнивать ее с другими фигурами или находить отношение площадей разных фигур. Например, можно сравнить площадь двух прямоугольников или найти отношение площади круга к площади квадрата, в который он вписан.

Основные понятия площади

Для нахождения площади прямоугольника необходимо умножить длину одной стороны на длину другой стороны. Формула для нахождения площади прямоугольника: S = a * b, где S – площадь, a и b – длины сторон.

Для нахождения площади квадрата необходимо возвести в квадрат длину одной из его сторон. Формула для нахождения площади квадрата: S = a^2, где S – площадь, a – длина стороны.

Для нахождения площади треугольника необходимо умножить половину основания на высоту. Формула для нахождения площади треугольника: S = (a * h) / 2, где S – площадь, a – длина основания, h – высота.

Вопрос-ответ:

Как определить площадь фигуры?

Площадь фигуры определяется путем измерения поверхности этой фигуры. Для прямоугольника, квадрата и параллелограмма площадь вычисляется как произведение длины и ширины. Для треугольника площадь вычисляется как половина произведения длины основания и высоты. Для круга площадь вычисляется как произведение числа Пи и квадрата радиуса.

Как вычислить площадь прямоугольника?

Для вычисления площади прямоугольника нужно умножить длину одной стороны на длину другой стороны.

Как вычислить площадь треугольника?

Площадь треугольника можно вычислить, умножив его базу (основание) на высоту, а затем разделив полученное значение на 2.

Как найти площадь квадрата?

Площадь квадрата можно найти, умножив длину его стороны на саму себя.

Что такое площадь круга?

Площадь круга — это количество пространства, занимаемого этим кругом. Она вычисляется по формуле: площадь = Пи * радиус^2, где Пи — математическая константа, примерно равная 3,14, а радиус — расстояние от центра круга до любой его точки.

Как определить площадь?

Площадь — это величина, которая показывает, сколько квадратных единиц может поместиться внутри фигуры. Для определения площади различных фигур используются разные формулы. Например, площадь прямоугольника можно найти, умножив длину на ширину.

Примеры расчета площади геометрических фигур

Для расчета площади различных геометрических фигур существуют формулы, которые можно применять для получения точного значения. Ниже приведены примеры расчета площади некоторых фигур:

• Прямоугольник:

Площадь прямоугольника вычисляется по формуле: S = a * b, где a — длина, b — ширина. Например, если длина прямоугольника равна 5 см, а ширина 3 см, то площадь будет равна 15 см2.

• Квадрат:

Площадь квадрата вычисляется по формуле: S = a2, где a — длина стороны. Например, если длина стороны квадрата равна 4 см, то площадь будет равна 16 см2.

• Треугольник:

Площадь треугольника вычисляется по формуле: S = 0.5 * a * h, где a — длина основания, h — высота, опущенная на основание. Например, если длина основания треугольника равна 6 см, а высота равна 8 см, то площадь будет равна 24 см2.

• Круг:

Площадь круга вычисляется по формуле: S = π * r2, где π (пи) — математическая константа, примерное значение 3.14, r — радиус. Например, если радиус круга равен 3 см, то площадь будет примерно равна 28.26 см2.

Это лишь несколько примеров расчета площади геометрических фигур. Для других фигур также существуют специальные формулы и методы расчета.

Квадрат и его площадь

Площадь квадрата можно вычислить, зная длину одной из его сторон. Формула для расчета площади квадрата очень проста: сторона квадрата возводится в квадрат. То есть, чтобы найти площадь квадрата, нужно умножить длину его стороны на саму себя.

Например, если сторона квадрата равна 5 см, то площадь квадрата будет равна 5 см × 5 см = 25 см².

Длина стороны квадрата (см)Площадь квадрата (см²)

2	4
3	9
4	16
5	25

Таким образом, площадь квадрата растет в квадрате от длины его стороны.

Прямоугольник и его площадь

Площадь прямоугольника вычисляется по формуле S = a * b, где S – площадь, a и b – длины сторон прямоугольника. Длина стороны прямоугольника называется основанием, а ширина – высотой. Площадь измеряется в квадратных единицах.

Например, если основание прямоугольника равно 5 см, а высота равна 7 см, то площадь можно вычислить по формуле S = 5 * 7 = 35 квадратных сантиметров.

Зная площадь прямоугольника и одну из его сторон, можно вычислить вторую сторону. Для этого нужно разделить площадь на известную сторону: b = S / a.

Площадь прямоугольника показывает, сколько квадратных единиц (например, квадратных сантиметров) занимает его поверхность. Знание площади прямоугольника важно при решении задач по различным областям жизни, например, при покупке ковра или расчете площади комнаты.

Треугольник и его площадь

Площадь треугольника — это величина, которая показывает, сколько плоской площади занимает треугольник. Площадь измеряется в квадратных единицах (например, квадратных сантиметрах или квадратных метрах).

Формула для вычисления площади треугольника зависит от известных данных о треугольнике:

• Если известны длины двух сторон треугольника и величина угла между ними, площадь можно найти по формуле: S = 0.5 * a * b * sin(угол), где a и b — длины сторон, а угол — величина угла.
• Если известны длины трех сторон треугольника, площадь можно вычислить по формуле Герона: S = sqrt(p * (p — a) * (p — b) * (p — c)), где p — полупериметр треугольника, а a, b и c — длины сторон.
• Если известны координаты вершин треугольника на плоскости, площадь можно найти с помощью формулы Гаусса: S = 0.5 * |(x1 — x3) * (y2 — y3) — (x2 — x3) * (y1 — y3)|, где x1, x2, x3, y1, y2, y3 — координаты вершин.

Зная площадь треугольника, можно решать различные задачи, связанные с этой геометрической фигурой, например, находить площадь других фигур, составленных из треугольников, или вычислять различные характеристики треугольника.

Круг и его площадь

Площадь круга — это количество плоскости, заключенной внутри круга. Обозначается символом S. Площадь круга можно вычислить по формуле:

S = πr²

где S — площадь круга, π (пи) — математическая константа, приближенное значение которой равно 3,14, а r — радиус круга, расстояние от его центра до любой точки на его окружности.

Например, если радиус круга равен 5 см, то площадь круга будет:

S = 3,14 × 5² = 3,14 × 25 = 78,5 см²

Таким образом, площадь круга с радиусом 5 см будет равна 78,5 см².