Что такое площадь и периметр в математике

Площадь и периметр — основные понятия в математике, которые используются для измерения и определения геометрических фигур. Площадь — это мера площади поверхности фигуры, а периметр — это сумма всех сторон фигуры. Узнайте, как рассчитывать площадь и периметр различных фигур и почему эти понятия важны для решения задач и практических проблем.

Площадь и периметр — два основных понятия в математике, которые помогают нам измерять и описывать геометрические фигуры. Они являются важными инструментами для практического применения математики в реальной жизни, а также становятся основой для более сложных математических концепций.

Периметр фигуры — это сумма длин всех её сторон. Он позволяет нам определить, насколько длинной будет окружность, если мы заменим фигуру на круг с тем же периметром. Периметр помогает измерить длину забора вокруг сада, или объём материала, необходимого для обрамления картинки в рамку.

Площадь фигуры — это мера её поверхности, обозначающая, сколько плоскости будет занимать эта фигура. Площадь позволяет нам определить, сколько травы нужно для покрытия поля, или какой объём краски необходим, чтобы покрасить стены комнаты. Она также может быть связана с количеством информации, которую можно разместить на поверхности фигуры.

Например, площадь квадрата можно вычислить, умножив длину его стороны на саму себя. Если сторона квадрата равна 5 единицам, то его площадь будет равна 25 квадратным единицам.

Таким образом, площадь и периметр являются фундаментальными понятиями в математике, которые позволяют нам измерять и описывать геометрические фигуры и применять их в практике. Понимание этих концепций помогает нам решать различные задачи и анализировать окружающий мир.

Понятие площади

Для простых фигур, таких как прямоугольник или квадрат, площадь можно легко найти, умножив длину на ширину. Например, площадь прямоугольника со сторонами 4 м и 6 м равна 24 м².

Однако, для более сложных фигур, таких как треугольник или круг, вычисление площади может быть более сложным. В таких случаях используются специальные формулы или методы, которые позволяют найти площадь этих фигур.

Понимание площади является важным в математике и других науках. Оно помогает нам измерять и сравнивать различные фигуры, а также решать практические задачи, связанные с площадью, например, расчет площади комнаты или поля.

Понятие периметра

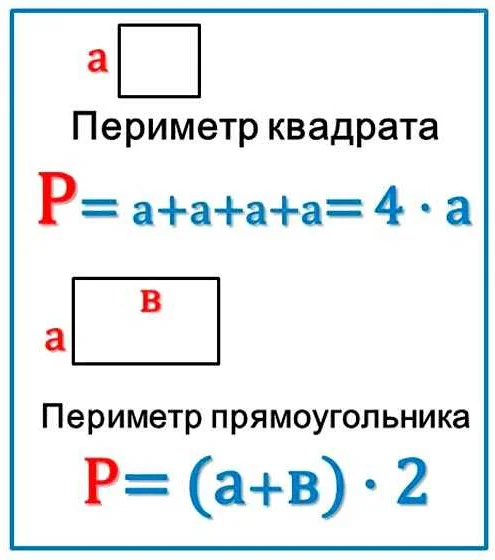
Для разных фигур формула для вычисления периметра может отличаться. Например, для прямоугольника периметр вычисляется по формуле:

Периметр = 2 * (длина + ширина)

Для круга периметр вычисляется по формуле:

Периметр = 2 * π * радиус

Знание периметра позволяет рассчитать длину ограды или периметр поля. Также периметр используется для оценки длины контура фигуры или для нахождения длины проволоки, необходимой для изготовления изделий.

Формулы для вычисления площади и периметра

Для вычисления площади и периметра различных геометрических фигур существуют соответствующие формулы. Рассмотрим некоторые из них:

1. Для вычисления площади прямоугольника можно использовать формулу:

ФигураФормула для площадиФормула для периметра

Прямоугольник

S = a * b

P = 2 * (a + b)

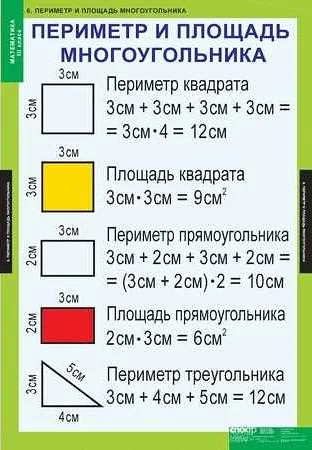
2. Для вычисления площади квадрата можно использовать формулу:

Квадрат

S = a * a

P = 4 * a

3. Для вычисления площади треугольника можно использовать формулу:

Треугольник

S = 0.5 * a * h

P = a + b + c

Где a, b, c — стороны фигуры, h — высота фигуры.

Это лишь некоторые примеры формул, используемых для вычисления площади и периметра различных геометрических фигур. В зависимости от формы фигуры могут быть использованы и другие формулы.

Примеры вычисления площади и периметра

Давайте рассмотрим несколько примеров, чтобы лучше понять, как вычислять площадь и периметр различных фигур.

Пример 1:

Рассмотрим прямоугольник со сторонами 4 и 6 единиц. Чтобы найти площадь этого прямоугольника, нужно умножить его длину на ширину: площадь = длина × ширина. В данном случае площадь будет равна 4 × 6 = 24 единицы квадратной. Чтобы найти периметр прямоугольника, нужно сложить все его стороны: периметр = 2 × (длина + ширина). В данном случае периметр будет равен 2 × (4 + 6) = 20 единиц.

Пример 2:

Рассмотрим квадрат со стороной 5 единиц. Площадь квадрата вычисляется также, как и площадь прямоугольника: площадь = сторона × сторона. В данном случае площадь будет равна 5 × 5 = 25 единиц квадратной. Периметр квадрата вычисляется по формуле: периметр = 4 × сторона. В данном случае периметр будет равен 4 × 5 = 20 единиц.

Пример 3:

Рассмотрим треугольник со сторонами 3, 4 и 5 единиц. Чтобы найти площадь треугольника, можно использовать формулу Герона: площадь = √(p × (p — a) × (p — b) × (p — c)), где p — полупериметр треугольника, а a, b и c — длины его сторон. В данном случае полупериметр будет равен (3 + 4 + 5) / 2 = 6 единиц. Подставляя значения в формулу, получим площадь = √(6 × (6 — 3) × (6 — 4) × (6 — 5)) = √(6 × 3 × 2 × 1) = √36 = 6 единиц квадратных. Периметр треугольника можно найти, сложив длины всех его сторон: периметр = a + b + c = 3 + 4 + 5 = 12 единиц.

Это лишь несколько примеров того, как вычислять площадь и периметр различных фигур. Зная соответствующие формулы, можно легко вычислить площадь и периметр любой фигуры.

Площадь и периметр в геометрических фигурах

Периметр — это сумма длин всех сторон фигуры. Он позволяет определить длину контура или окружности фигуры. Например, для прямоугольника периметр равен удвоенной сумме длин его сторон.

Пример:

У прямоугольника со сторонами 4 см и 6 см периметр будет равен: 2 * (4 + 6) = 2 * 10 = 20 см.

Площадь — это мера площади поверхности, заключенной внутри контура фигуры. Она позволяет определить, сколько пространства занимает геометрическая фигура. Например, для прямоугольника площадь равна произведению длины и ширины.

Пример:

У прямоугольника со сторонами 4 см и 6 см площадь будет равна: 4 * 6 = 24 см².

Площадь и периметр имеют различные формулы для разных геометрических фигур. Например, для треугольника с известными сторонами можно использовать формулу Герона, а для круга — формулы площади и периметра окружности.

Зависимость площади и периметра от размеров фигуры

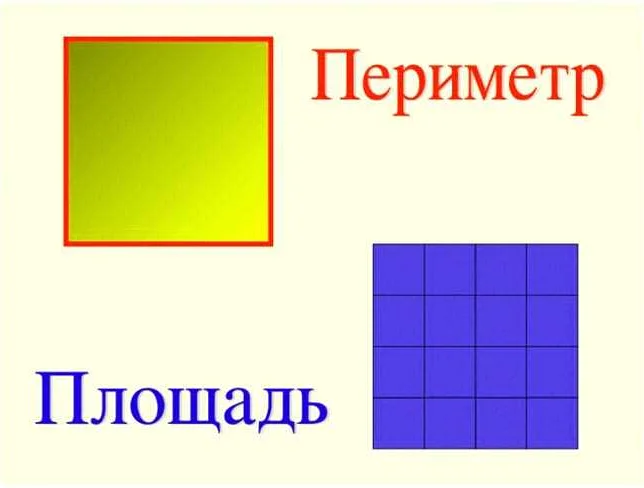
Для некоторых фигур, таких как прямоугольник или квадрат, существует простая формула для вычисления площади и периметра. Например, площадь прямоугольника равна произведению длины и ширины, а периметр – удвоенной сумме длины и ширины:

• Площадь прямоугольника: S = a * b
• Периметр прямоугольника: P = 2 * (a + b)

Для других фигур, таких как круг или треугольник, формулы для вычисления площади и периметра сложнее. Например, площадь круга вычисляется по формуле π * r^2, где π – это число Пи (приблизительно равное 3,14), а r – радиус круга. Периметр треугольника может быть вычислен как сумма длин его сторон.

Таким образом, размеры фигуры непосредственно влияют на ее площадь и периметр. Изменение длины, ширины, радиуса или сторон фигуры приведет к изменению ее площади и периметра. Это позволяет легко сравнивать фигуры и использовать понятия площади и периметра в различных математических задачах.

Практическое применение площади и периметра

Понимание площади и периметра имеет важное практическое применение в различных сферах жизни. Вот несколько примеров:

1. Строительство: при проектировании зданий и сооружений необходимо учитывать площадь и периметр для определения размеров и площади пола, стен и крыши.
2. Архитектура: архитекторы используют площадь и периметр для расчета объемов материалов, необходимых для строительства зданий, а также для создания эстетически приятных пропорций и форм.
3. Ландшафтный дизайн: при оформлении садов, парков и других ландшафтов площадь и периметр помогают определить размеры газонов, клумб, дорожек и других элементов.
4. Торговля: в розничной торговле площадь используется для расчета арендной платы за аренду помещений, а периметр — для определения длины витрин и прилавков.
5. Инженерия: инженеры используют площадь и периметр для расчета объемов материалов и нужного пространства при проектировании различных инженерных систем, таких как водопровод и электроснабжение.

Это лишь несколько примеров из множества областей, где понимание площади и периметра имеет практическое значение. Знание этих концепций помогает решать реальные задачи, связанные с размерами и площадью объектов.

Вопрос-ответ:

Что такое площадь?

Площадь — это мера, которая определяет, сколько плоскостей занимает фигура. Она измеряется в квадратных единицах, таких как квадратные метры или квадратные сантиметры. Площадь может быть вычислена для различных фигур, включая квадраты, прямоугольники, треугольники и круги.

Как вычислить площадь квадрата?

Для вычисления площади квадрата нужно умножить длину одной стороны на длину другой стороны. Например, если сторона квадрата равна 5 сантиметров, то площадь будет равна 5 сантиметров умножить на 5 сантиметров, то есть 25 квадратных сантиметров.

Что такое периметр?

Периметр — это длина внешней границы фигуры. Он измеряется в единицах длины, таких как сантиметры или метры. Периметр может быть вычислен для различных фигур, включая квадраты, прямоугольники, треугольники и круги.

Как вычислить периметр прямоугольника?

Для вычисления периметра прямоугольника нужно сложить длины всех его сторон. Например, если длина прямоугольника равна 5 сантиметров, а ширина равна 3 сантиметра, то периметр будет равен 5 сантиметров плюс 3 сантиметра плюс 5 сантиметров плюс 3 сантиметра, то есть 16 сантиметров.

Как вычислить площадь треугольника?

Для вычисления площади треугольника можно использовать формулу: площадь равна половине произведения длины основания треугольника на высоту, опущенную на это основание. Например, если основание треугольника равно 6 сантиметров, а высота равна 4 сантиметрам, то площадь будет равна половине произведения 6 сантиметров на 4 сантиметра, то есть 12 квадратных сантиметров.

Что такое площадь?

Площадь — это мера площади поверхности. В математике площадь определяется как количество квадратных единиц, которые могут поместиться на данной поверхности. Например, площадь квадрата равна длине его стороны, возведенной в квадрат.

Видео по теме: