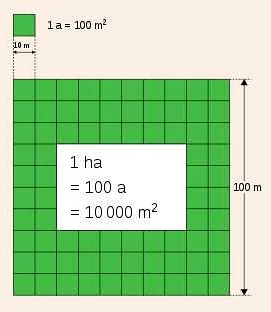
Что такое площадь в математике

Площадь в математике — это мера поверхности фигуры. Она определяется как количество единичных квадратных единиц, которые полностью покрывают данную фигуру. Узнайте основные понятия и формулы для вычисления площади различных геометрических фигур.

Площадь — это важное понятие в математике, которое используется для измерения площади поверхности фигуры или объекта. Площадь является одним из основных параметров, которые помогают определить размеры и характеристики объектов в пространстве. В математике площадь измеряется в квадратных единицах, таких как квадратные метры, квадратные сантиметры или квадратные дюймы.

Расчет площади зависит от формы и размеров объекта. Для простых геометрических фигур, таких как прямоугольник или круг, существуют стандартные формулы, которые позволяют быстро и точно определить их площадь. Однако, для более сложных фигур, таких как треугольник или многоугольник, требуется применение специальных формул и методов расчета.

Например, для прямоугольника площадь можно найти, умножив длину на ширину. Для круга площадь вычисляется по формуле S = πr^2, где π — математическая константа, а r — радиус круга.

Площадь играет важную роль в различных областях, начиная от геометрии и архитектуры до естественных наук и инженерии. Она позволяет определить площади поверхностей земли, строений, фигур и других объектов. Расчет площади также полезен при решении задач по обмену и упаковке материалов, определении площади поля для сельского хозяйства и многих других практических ситуациях.

Определение площади в математике

В математике площадь обычно измеряется в квадратных единицах, таких как квадратные метры (м²) или квадратные сантиметры (см²). Однако, в зависимости от конкретной задачи, площадь может быть измерена и в других единицах.

Площадь может быть вычислена для различных геометрических фигур, таких как треугольники, прямоугольники, круги и многоугольники. Для каждой фигуры существуют специальные формулы и методы, позволяющие рассчитать ее площадь.

Понимание и умение вычислять площадь являются важными навыками в различных областях, включая архитектуру, строительство, географию, физику и экономику.

Как измеряется площадь

Для измерения площади используются различные единицы измерения, в зависимости от конкретной фигуры и ее размеров. Например, для прямоугольника площадь измеряется в квадратных единицах длины (например, квадратных метрах или квадратных сантиметрах). Для треугольника площадь измеряется в квадратных единицах длины, но формула для ее расчета отличается от формулы для прямоугольника.

Существует несколько способов измерения площади. Один из наиболее распространенных – это геометрический подход, когда площадь фигуры вычисляется на основе ее геометрических характеристик, таких как длины сторон, углы и радиусы.

Еще один способ измерения – это метод покрытия, когда площадь фигуры определяется путем покрытия ее поверхности определенным количеством единичных квадратных единиц.

Независимо от способа измерения, площадь является важным понятием в математике и имеет множество приложений в реальной жизни. Она используется при решении задач строительства, расчета площадей полей и участков земли, а также в географии, физике и других науках.

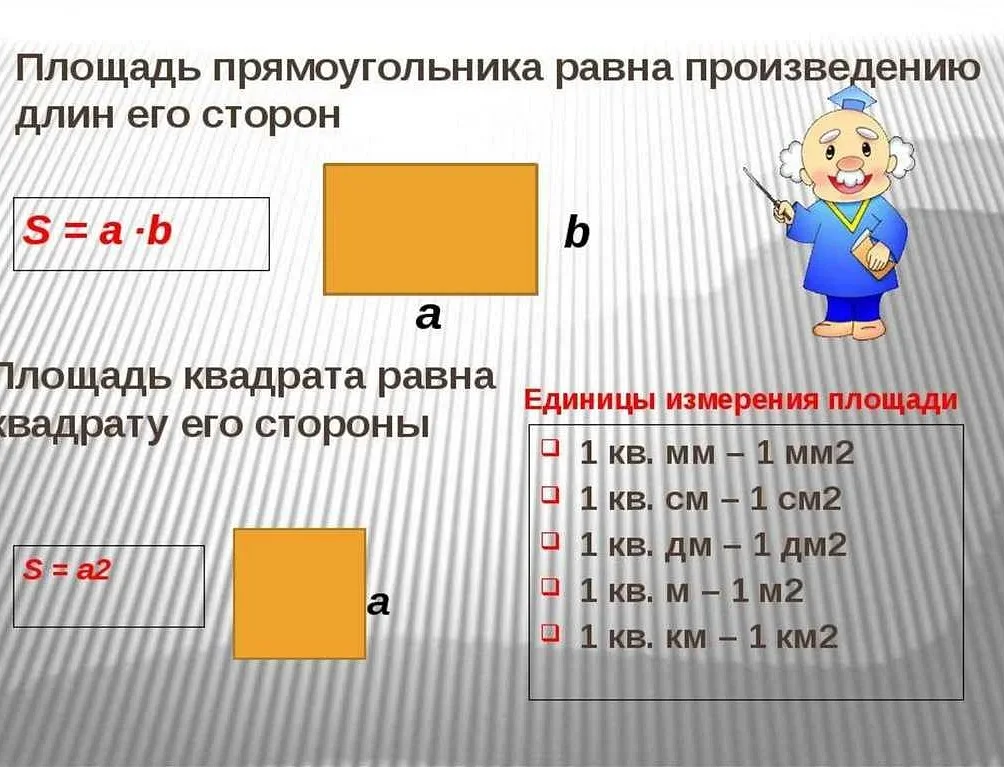
Примеры расчета площади прямоугольника

Пример 1:

• Дан прямоугольник со сторонами 5 см и 10 см.
• Чтобы найти площадь прямоугольника, умножим длину одной стороны на длину другой стороны: 5 см * 10 см = 50 см².
• Площадь прямоугольника равна 50 квадратным сантиметрам.

Пример 2:

• Дан прямоугольник со сторонами 8 м и 6 м.
• Чтобы найти площадь прямоугольника, умножим длину одной стороны на длину другой стороны: 8 м * 6 м = 48 м².
• Площадь прямоугольника равна 48 квадратным метрам.

Пример 3:

• Дан прямоугольник со сторонами 3 дм и 4 дм.
• Чтобы найти площадь прямоугольника, умножим длину одной стороны на длину другой стороны: 3 дм * 4 дм = 12 дм².
• Площадь прямоугольника равна 12 квадратным дециметрам.

Таким образом, площадь прямоугольника вычисляется как произведение длины одной стороны на длину другой стороны и измеряется в квадратных единицах соответствующей размерности.

Примеры расчета площади треугольника

Площадь треугольника можно рассчитать с помощью различных формул, в зависимости от известных данных. Вот несколько примеров:

ПримерИзвестные данныеФормулаРезультат

Пример 1	Основание: 8 см Высота: 5 см	(Основание * Высота) / 2	20 кв. см
Пример 2	Сторона A: 6 см Сторона B: 4 см Угол между сторонами A и B: 60 градусов	(A * B * sin(Угол)) / 2	8.31 кв. см
Пример 3	Сторона A: 15 см Сторона B: 13 см Сторона C: 10 см	√(p * (p — A) * (p — B) * (p — C)) p = (A + B + C) / 2	58.78 кв. см

Это лишь несколько примеров расчета площади треугольника. В математике существует множество других формул, которые позволяют найти площадь треугольника при различных условиях. Важно выбрать подходящую формулу в зависимости от имеющихся данных и применить ее для получения точного результата.

Примеры расчета площади круга

Площадь круга можно вычислить по формуле:

S = π * r2,

где S — площадь круга, π — число Пи (приближенно равно 3,14), r — радиус круга.

Например, пусть радиус круга равен 5 см. Тогда площадь круга можно вычислить следующим образом:

S = 3,14 * 52 = 3,14 * 25 = 78,5 (квадратные сантиметры).

Таким образом, площадь круга с радиусом 5 см равна 78,5 квадратных сантиметров.

Другой пример. Пусть радиус круга равен 8 м. Тогда площадь круга можно вычислить следующим образом:

S = 3,14 * 82 = 3,14 * 64 = 200,96 (квадратных метров).

Таким образом, площадь круга с радиусом 8 м равна 200,96 квадратных метров.

Примеры расчета площади параллелограмма

Пример 1:

Дано: сторона параллелограмма a = 5 см, высота h = 8 см.

Чтобы найти площадь параллелограмма, нужно умножить длину одной стороны на высоту, т.е. S = a * h.

Подставляя значения, получаем S = 5 см * 8 см = 40 см².

Ответ: площадь параллелограмма равна 40 см².

Пример 2:

Дано: длина одной стороны параллелограмма a = 9 м, длина другой стороны b = 6 м, угол между сторонами α = 60°.

Чтобы найти площадь параллелограмма, нужно умножить длину одной стороны на длину другой стороны и на синус угла между ними, т.е. S = a * b * sin(α).

Подставляя значения, получаем S = 9 м * 6 м * sin(60°) ≈ 27 м².

Ответ: площадь параллелограмма примерно равна 27 м².

Примеры расчета площади трапеции

Для расчета площади трапеции необходимо знать ее основания и высоту. Рассмотрим несколько примеров:

1. Пример 1:

   Трапеция с основаниями длиной 5 см и 9 см, высота равна 4 см.

   Формула для расчета площади трапеции: S = (a + b) * h / 2, где a и b — длины оснований, h — высота.

   Подставляя значения в формулу, получаем: S = (5 + 9) * 4 / 2 = 14.

   Площадь трапеции равна 14 квадратным сантиметрам.

2. Пример 2:

   Трапеция с основаниями длиной 6 м и 8 м, высота равна 3 м.

   Используем ту же формулу: S = (a + b) * h / 2.

   Подставляя значения в формулу, получаем: S = (6 + 8) * 3 / 2 = 21.

   Площадь трапеции равна 21 квадратному метру.

3. Пример 3:

   Трапеция с основаниями длиной 10 см и 15 см, высота равна 6 см.

   Снова подставляем значения в формулу: S = (a + b) * h / 2.

   Получаем: S = (10 + 15) * 6 / 2 = 75.

   Площадь трапеции равна 75 квадратным сантиметрам.

Таким образом, площадь трапеции можно найти, зная длины ее оснований и высоту, используя соответствующую формулу.

Вопрос-ответ:

Что такое площадь в математике?

Площадь в математике — это мера двумерной фигуры, которая показывает, сколько плоского пространства занимает эта фигура. Она измеряется в квадратных единицах.

Как можно рассчитать площадь прямоугольника?

Для расчета площади прямоугольника необходимо умножить длину одной из сторон на длину другой стороны. Формула для расчета площади прямоугольника: S = a * b, где S — площадь, а и b — длины сторон прямоугольника.

Как рассчитать площадь круга?

Для расчета площади круга необходимо умножить квадрат радиуса на число пи (π). Формула для расчета площади круга: S = π * r^2, где S — площадь, π — число пи (приближенное значение 3,14), r — радиус круга.

Как найти площадь треугольника?

Для расчета площади треугольника необходимо умножить половину основания на высоту треугольника. Формула для расчета площади треугольника: S = (a * h) / 2, где S — площадь, a — основание треугольника, h — высота треугольника, проведенная к основанию.

Как рассчитать площадь фигуры, состоящей из нескольких прямоугольников?

Если фигура состоит из нескольких прямоугольников, то для расчета площади необходимо сложить площади всех прямоугольников в этой фигуре. Например, если фигура состоит из двух прямоугольников, то площадь будет равна сумме площадей этих двух прямоугольников.

Как определить площадь прямоугольника?

Площадь прямоугольника можно определить, умножив длину одной из его сторон на длину другой стороны. Например, если длина прямоугольника равна 5 см, а ширина равна 3 см, то площадь равна 5 см * 3 см = 15 см².

Как определить площадь круга?

Площадь круга можно определить по формуле S = π * r², где S — площадь, π — математическая константа, примерно равная 3,14, а r — радиус круга. Например, если радиус круга равен 2 см, то площадь равна 3,14 * 2² = 12,56 см².

Видео по теме: