Что такое подобные слагаемые в математике

Подобные слагаемые в математике — это слагаемые, которые имеют одинаковые переменные и степени. Примеры и объяснения подобных слагаемых в математике.

В математике понятие «подобные слагаемые» является одним из основных при изучении алгебры и арифметики. Подобные слагаемые — это слагаемые, которые имеют одинаковые переменные и степени этих переменных. Они могут отличаться только коэффициентами перед этими переменными.

Для наглядного представления понятия «подобные слагаемые» рассмотрим пример. Пусть у нас есть выражение 3x + 2y + 5x + 4y. В этом выражении слагаемые 3x и 5x являются подобными, так как они имеют одну и ту же переменную x и одинаковые степени этой переменной. Аналогично, слагаемые 2y и 4y также являются подобными, так как они имеют переменную y и одинаковую степень этой переменной.

Подобные слагаемые могут быть складываны и вычитаться друг из друга, при этом переменные и их степени сохраняются, а коэффициенты складываются или вычитаются. Например, если у нас есть выражение 3x + 5x, то результатом сложения подобных слагаемых будет 8x. А если у нас есть выражение 4y — 2y, то результатом вычитания подобных слагаемых будет 2y.

Понимание понятия «подобные слагаемые» является важным для работы с алгебраическими выражениями и упрощения математических задач. Знание правил сложения и вычитания подобных слагаемых позволяет упростить выражения и находить их значения.

Понятие подобных слагаемых

Например, в выражении 3x^2 + 2xy + 5x^2 + 4xy — 2x^2, слагаемые 3x^2, 5x^2 и -2x^2 являются подобными, так как у них одинаковые переменные (x) и одинаковые степени (2).

Подобные слагаемые могут быть сокращены, то есть объединены в одно слагаемое, путем сложения или вычитания их коэффициентов. В примере выше, подобные слагаемые 3x^2, 5x^2 и -2x^2 могут быть сокращены до 6x^2.

Понимание понятия подобных слагаемых является важным в алгебре и математике в целом, так как оно позволяет упрощать и решать сложные уравнения и выражения.

Видео по теме:

Условия для слагаемых, чтобы они были подобными

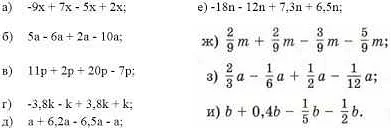
Две или более слагаемых называются подобными, если они имеют одинаковые переменные и степени этих переменных.

Для того чтобы слагаемые были подобными, они должны удовлетворять следующим условиям:

1. Одинаковые переменные: подобные слагаемые должны содержать одни и те же переменные. Например, если у одного слагаемого есть переменная x, то и у других слагаемых должна быть переменная x.
2. Одинаковые степени переменных: подобные слагаемые должны иметь одинаковые степени переменных. Например, если у одного слагаемого переменная x имеет степень 2, то и у других слагаемых переменная x должна иметь степень 2.

Например, в выражении 2x^2 + 3x^2 + 4x + 5, слагаемые 2x^2 и 3x^2 являются подобными, так как они содержат одну и ту же переменную x и имеют одинаковую степень переменной x. Слагаемое 4x не является подобным слагаемым, так как оно содержит переменную x, но имеет степень переменной, отличную от степени переменной в подобных слагаемых. Слагаемое 5 не является подобным слагаемым, так как оно не содержит переменную x.

Операции с подобными слагаемыми

Подобные слагаемые можно суммировать и вычитать, выполняя следующие операции:

1. Сложение подобных слагаемых:

Для сложения подобных слагаемых нужно сложить их числовые коэффициенты, оставляя неизменным общий множитель (если он есть).

Например, если у нас есть выражение 3x + 2x, то мы можем сложить коэффициенты x и получим 5x.

2. Вычитание подобных слагаемых:

Для вычитания подобных слагаемых нужно вычесть их числовые коэффициенты, оставляя неизменным общий множитель (если он есть).

Например, если у нас есть выражение 4y — 2y, то мы можем вычесть коэффициенты y и получим 2y.

3. Умножение подобных слагаемых:

Умножение подобных слагаемых выполняется путем умножения их числовых коэффициентов и умножения общих множителей (если они есть).

Например, если у нас есть выражение 2a * 3a, то мы можем умножить коэффициенты 2 и 3, а также умножить множители a и получим 6a^2 (a в квадрате).

4. Деление подобных слагаемых:

Деление подобных слагаемых выполняется путем деления их числовых коэффициентов и деления общих множителей (если они есть).

Например, если у нас есть выражение 10b^2 / 5b, то мы можем поделить коэффициенты 10 и 5, а также поделить множители b и получим 2b (b в первой степени).

Важно помнить, что при выполнении операций с подобными слагаемыми нужно учитывать их общий множитель и числовые коэффициенты, чтобы получить правильный результат.

Вопрос-ответ:

Что такое подобные слагаемые в математике?

Подобные слагаемые — это слагаемые, которые содержат одинаковые буквенные выражения, включая степень и коэффициент.

Как определить, что слагаемые являются подобными?

Чтобы определить, что слагаемые являются подобными, нужно сравнить их буквенные выражения. Если выражения совпадают, то слагаемые являются подобными.

Какие примеры подобных слагаемых можно привести?

Примеры подобных слагаемых: 3x^2 и 5x^2, 2y и -8y, 7z^3 и -3z^3. Во всех этих примерах буквенные выражения совпадают, поэтому слагаемые являются подобными.

Зачем нужно выделять подобные слагаемые?

Выделение подобных слагаемых позволяет упростить выражение и выполнить операции над ними. Например, сложение или вычитание подобных слагаемых проще, чем работа с неупрощенными выражениями.

Какие правила существуют для работы с подобными слагаемыми?

Для работы с подобными слагаемыми можно использовать правила сложения и вычитания. При сложении (или вычитании) подобных слагаемых, коэффициенты складываются (или вычитаются), а буквенные выражения остаются неизменными.

Что такое подобные слагаемые?

Подобные слагаемые — это слагаемые, которые имеют одинаковые буквенные выражения и одинаковые степени переменных. Например, 3x и -2x являются подобными слагаемыми, так как оба содержат переменную x с одинаковой степенью.

Примеры подобных слагаемых

Рассмотрим несколько примеров подобных слагаемых:

Пример 1:

4x + 2x

В данном примере подобные слагаемые – это 4x и 2x, так как они оба содержат переменную x. Можно объединить эти слагаемые, складывая их коэффициенты, и получить:

4x + 2x = 6x

Пример 2:

3y^2 — 2y^2

В этом примере подобные слагаемые – это 3y^2 и -2y^2, так как они оба содержат переменную y в степени 2. Можно объединить эти слагаемые, складывая их коэффициенты, и получить:

3y^2 — 2y^2 = y^2

Пример 3:

7a^3b — 5a^3b

В данном примере подобные слагаемые – это 7a^3b и -5a^3b, так как они оба содержат переменные a в степени 3 и b. Можно объединить эти слагаемые, складывая их коэффициенты, и получить:

7a^3b — 5a^3b = 2a^3b

Таким образом, подобные слагаемые позволяют упрощать выражения, объединяя их в одно слагаемое и упрощая математические вычисления.

Задачи на нахождение подобных слагаемых

Задачи на нахождение подобных слагаемых в математике позволяют упражняться в определении и суммировании слагаемых, имеющих одинаковые переменные и степени. Решение таких задач требует внимательности и навыков работы с алгебраическими выражениями.

Приведем несколько примеров задач на нахождение подобных слагаемых:

1. Упростите выражение: 3x + 5x — 2x.
2. Найдите сумму: 2a^2b + 3ab — a^2b + 4ab^2.
3. Выразите выражение в общем виде: nx^2 — mx^2 + px^2.

Для решения подобных задач необходимо:

• Определить переменные и их степени в каждом слагаемом.
• Сгруппировать слагаемые с одинаковыми переменными и степенями.
• Сложить или вычесть полученные группы слагаемых.

В первом примере задачи необходимо сложить слагаемые с одинаковыми переменными и степенями: 3x + 5x — 2x = (3 + 5 — 2)x = 6x.

Во втором примере необходимо сгруппировать слагаемые с одинаковыми переменными и степенями: 2a^2b + 3ab — a^2b + 4ab^2 = (2a^2b — a^2b) + (3ab + 4ab^2) = a^2b + 7ab^2.

В третьем примере задачи необходимо выразить выражение в общем виде, сгруппировав слагаемые с одинаковыми переменными и степенями: nx^2 — mx^2 + px^2 = (n — m + p)x^2.

Решение задач на нахождение подобных слагаемых помогает развить навыки работы с алгебраическими выражениями и позволяет лучше понять принципы суммирования и упрощения выражений.

Практическое применение подобных слагаемых

Подобные слагаемые в математике широко применяются в различных областях науки и техники. Они помогают упростить выражения и решать задачи более эффективно. Вот несколько примеров практического применения подобных слагаемых:

1. Физика

Подобные слагаемые используются при решении задач на механику, электродинамику и другие разделы физики. Например, при анализе движения тела с постоянным ускорением можно выделить подобные слагаемые в уравнении движения, что позволяет более просто определить закон движения и решить задачу.

2. Финансы

В финансовой математике подобные слагаемые используются при расчете сложных процентов, а также при анализе инвестиций и кредитов. Например, при расчете сложных процентов на банковский вклад можно выделить подобные слагаемые в формуле для расчета итоговой суммы.

3. Компьютерная графика

В компьютерной графике подобные слагаемые используются для моделирования и отображения трехмерных объектов. Например, при задании координат вершин трехмерной модели можно выделить подобные слагаемые для упрощения вычислений и ускорения отрисовки.

Таким образом, понимание и использование подобных слагаемых позволяет упростить и эффективно решать различные математические задачи в различных областях науки и техники.

Значение подобных слагаемых в алгебре

Подобные слагаемые особенно важны при выполнении операций сложения и вычитания многочленов. При сложении многочленов, слагаемые с одинаковыми переменными и их степенями объединяются и записываются в итоговом многочлене один раз суммой их коэффициентов. Такой процесс называется упрощением многочлена.

Например, рассмотрим многочлены:

3x + 2y + 5x + 4y

2x^2 — 3y^2 + x^2 + 2y^2

В первом многочлене, у нас есть два подобных слагаемых: 3x и 5x, а также 2y и 4y. Они могут быть объединены в одно слагаемое: 8x и 6y. Таким образом, первый многочлен может быть упрощен до:

8x + 6y

Во втором многочлене, у нас также есть два подобных слагаемых: 2x^2 и x^2, а также -3y^2 и 2y^2. Они могут быть объединены в одно слагаемое: 3x^2 и -y^2. Таким образом, второй многочлен может быть упрощен до:

3x^2 — y^2

Такое упрощение позволяет нам более удобно работать с многочленами и выполнять алгебраические операции, такие как сложение, вычитание и умножение.

Выводы о подобных слагаемых

Основные выводы о подобных слагаемых:

1. Сложение и вычитание подобных слагаемых. При сложении или вычитании подобных слагаемых, мы складываем или вычитаем их числовые коэффициенты, при этом переменные и показатели степеней остаются неизменными.

2. Упрощение выражений. Если в выражении присутствуют несколько подобных слагаемых, их можно упростить, собрав их вместе. Для этого, мы складываем или вычитаем их числовые коэффициенты и оставляем переменные и показатели степеней без изменений.

3. Умножение подобных слагаемых. При умножении двух подобных слагаемых, мы умножаем их числовые коэффициенты и перемножаем переменные соответствующих показателей степеней, получая новое подобное слагаемое.

4. Деление подобных слагаемых. При делении одного подобного слагаемого на другое, мы делим их числовые коэффициенты и делим переменные соответствующих показателей степеней, получая новое подобное слагаемое.

5. Примеры подобных слагаемых. Например, в выражении 2x^2 + 3y^2 — 5x^2 + 4y^2, слагаемые 2x^2 и -5x^2 являются подобными, так как обе они имеют переменную x с показателем степени 2. Аналогично, слагаемые 3y^2 и 4y^2 являются подобными, так как обе они имеют переменную y с показателем степени 2.