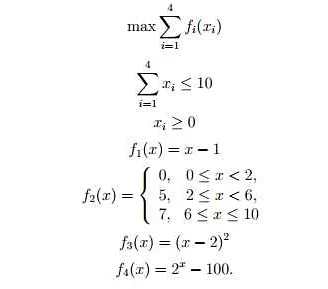Фиктивные переменные в дискретной математике: что это и зачем нужны?

Фиктивные переменные в дискретной математике — это способ введения дополнительных переменных для удобства решения задач. Узнайте, как они применяются в различных областях математики и как их можно использовать в своих исследованиях.

Дискретная математика – это раздел математики, который изучает объекты, состоящие из отдельных и отделимых элементов. Она находит свое применение в разных сферах науки и техники: от компьютерной науки и теории алгоритмов до теории игр и криптографии. Одним из важных понятий дискретной математики являются фиктивные переменные — особые объекты, которые позволяют решать сложные задачи в теории отношений.

Фиктивные переменные – это искусственные переменные, которые отражаются в теории на термины предикатов. Они используются в теории отношений для упрощения вычислений и замены сложных формул более простыми. Многие задачи в теории отношений становятся более простыми и понятными, когда мы использовали фиктивные переменные.

Зачастую понимание фиктивных переменных требует некоторых знаний по теории отношений и предикатов, поэтому многие сталкиваются с трудностями в их изучении. В этой статье мы попытаемся осветить все основные аспекты фиктивных переменных, предоставить их объяснения и привести примеры.

Что такое фиктивные переменные

Фиктивные переменные являются ключевым элементом в дискретной математике и используются для различных целей. Они представляют собой особый тип переменных, который не несет реальной информации, а используется для удобства решения задач.

Одним из основных применений фиктивных переменных является удобство записи логических формул и уравнений. Используя фиктивные переменные, можно сделать запись формул и уравнений более лаконичной и понятной, а также упростить их решение.

Фиктивные переменные также широко применяются в теории автоматов и теории кодирования. В этих областях они используются, например, для упрощения алгоритмов и описания кодов.

В стандартной литературе по дискретной математике фиктивные переменные часто называются также «вспомогательными переменными» или «промежуточными переменными». Данные термины также используются для обозначения этого концепта.

Видео по теме:

Зачем они нужны

Фиктивные переменные — это важный инструмент в дискретной математике, который используется для решения различных задач, связанных с логическими выражениями. Они позволяют создавать таблицы истинности и описывать логические операции с более чем двумя переменными.

Фиктивные переменные могут быть использованы для создания более эффективных алгоритмов и упрощения логических выражений. Они могут также служить механизмом для сокращения количества условных операторов в программировании.

Например, использование фиктивных переменных может помочь при построении алгоритма для нахождения максимального элемента из набора данных. Вместо того, чтобы использовать несколько условных операторов, можно использовать фиктивные переменные для уменьшения количества операторов и совершения вычислений быстрее.

Фиктивные переменные также могут использоваться для анализа сложных логических выражений с большим количеством переменных. Они помогают организовать вычисления и упростить выражения, облегчая понимание функционирования системы и нахождение ее ошибок.

Какие примеры применения есть в реальной жизни

Фиктивные переменные находят применение во многих областях реальной жизни. Одним из примеров является работа с базами данных. Если одно из полей имеет множество значений, эти значения можно заменить на фиктивные переменные, что ускорит обработку данных и сократит объем хранимой информации.

Другим примером является использование фиктивных переменных в машинном обучении. При создании моделей машинного обучения, фиктивные переменные могут использоваться для представления различных категорий данных, как, например, типа продукта или цвета кожи. Это упрощает создание моделей и увеличивает точность результатов.

Еще одним примером применения фиктивных переменных является учет влияния различных факторов на результаты исследований. Например, при исследовании влияния образования на заработную плату, фиктивные переменные можно использовать для учета различных факторов, таких как опыт работы и специализация.

В целом, фиктивные переменные являются важным инструментом для работы с категориальными данными, которые встречаются во многих областях, от экономики и политики до машинного обучения и науки о данных.

Вопрос-ответ:

Что такое фиктивная переменная в дискретной математике?

Фиктивная переменная — это переменная, имеющая только два возможных значения (0 или 1) и несущая дополнительную информацию в логических выражениях. Она не является истинной переменной и используется только для удобства построения логических выражений.

Как использование фиктивных переменных может улучшить логическое выражение?

Использование фиктивных переменных может помочь упростить логическое выражение и сделать его более понятным для анализа. Они могут быть использованы для соединения двух логических переменных или условий в более сложное выражение.

Как можно определить количество фиктивных переменных, которые необходимы для определенного логического выражения?

Количество фиктивных переменных, необходимых для определенного логического выражения, зависит от сложности выражения и структуры задачи. Обычно можно определить оптимальное количество фиктивных переменных, используя метод Карно и алгоритмы минимизации.

Какие преимущества могут получиться при использовании фиктивных переменных в некоторых задачах?

Использование фиктивных переменных может сделать проблему более понятной и структурированной, помочь анализировать выражение и оптимизировать его. Это может привести к лучшим решениям и эффективности в работе с большими и сложными системами.

Как можно определить, когда использование фиктивных переменных является наиболее эффективным?

Использование фиктивных переменных имеет смысл только если оно позволяет упростить выражение или решить задачу более эффективно. Для определения наиболее эффективного использования фиктивных переменных необходимо провести анализ структуры проблемы и определить, какие переменные и условия оказываются наиболее сложными для анализа и оптимизации.

Какая роль фиктивных переменных в логическом анализе?

Фиктивные переменные могут использоваться для улучшения эффективности и точности логического анализа. Они могут помочь упростить логические выражения и значительно сократить время, необходимое для анализа данного выражения.

Есть ли ограничения в использовании фиктивных переменных в дискретной математике?

В использовании фиктивных переменных есть некоторые ограничения, которые следует учитывать. Например, чрезмерное использование фиктивных переменных может привести к более сложным выражениям и медленному выполнению программы. Кроме того, необходимо убедиться в том, что использование фиктивных переменных не приводит к ошибкам в логическом анализе или решении задачи.

Какие типы фиктивных переменных бывают

Фиктивные переменные — это переменные, которые используются для преобразования категориальных данных в числовые значения или для создания дополнительных факторов для анализа. Они могут быть разных типов в зависимости от задачи, которую необходимо решить.

Бинарные фиктивные переменные

Бинарная фиктивная переменная может принимать только два значения: 0 или 1. Они часто используются в логистической регрессии, чтобы преобразовать категориальные переменные в числовые. Например, если у нас есть переменная «пол», мы можем создать бинарную фиктивную переменную, которая будет равна 1, если это женский пол, и равна 0, если это мужской пол.

Номинальные фиктивные переменные

Номинальные фиктивные переменные используются, когда данные не имеют порядка. Такие переменные могут быть преобразованы в k-1 фиктивных переменных, где k — число категорий. Например, если у нас есть переменная «город», которая может иметь три значения: Москва, Санкт-Петербург, Казань, то мы можем создать две номинальных фиктивных переменных city1 и city2. city1 будет равен 1, если город – Москва, и 0 в противном случае; city2 будет равен 1, если город – Санкт-Петербург, и 0 в противном случае.

Упорядоченные фиктивные переменные

Упорядоченные фиктивные переменные используются, когда данные имеют порядок. Например, если мы анализируем образование, которое имеет уровни от начального до высшего, мы можем создать упорядоченные фиктивные переменные, чтобы учитывать порядок образования. Фиктивные переменные будут иметь значения либо 0, либо 1, причем каждая более высокая переменная будет равна 1, если всех предыдущих переменных (более низких уровней) равны 1.

Интерактивные фиктивные переменные

Интерактивные фиктивные переменные используются, чтобы выявить взаимодействие между переменными. Если мы хотим проверить, влияет ли образование и пол на зарплату, мы можем создать две интерактивные фиктивные переменные: мужской пол и образование, женский пол и образование. Каждый из них будет принимать значения 0 или 1, в зависимости от значения образования и пола.

Различные типы фиктивных переменных могут быть использованы в разных задачах и иметь разное применение. Таким образом фиктивные переменные являются важными инструментами для преобразования категориальных данных в числовые значения, что позволяет проводить статистический анализ и моделирование.

Как правильно задавать фиктивные переменные

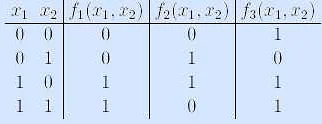
Фиктивные переменные — это переменные, которые добавляются к системе уравнений искусственно, чтобы определить ее совместность или несовместность. Для того, чтобы правильно задать фиктивную переменную необходимо:

• Выбрать правильное количество переменных: количество фиктивных переменных необходимо выбирать в зависимости от количества уравнений системы. Если количество уравнений системы больше, чем количество переменных, то необходимо добавить фиктивные переменные, чтобы система стала совместной.
• Выбрать правильный знак при фиктивной переменной: знак при фиктивной переменной выбирается в зависимости от знака свободного члена. Если свободный член положительный — знак при фиктивной переменной должен быть отрицательным. Если свободный член отрицательный — знак при фиктивной переменной должен быть положительным.
• Выбрать правильную начальную точку: начальное значение фиктивной переменной зависит от других переменных в системе. Оно должно быть выбрано так, чтобы система оставалась совместной. Для этого необходимо решить систему без фиктивных переменных и выбрать значения переменных, которые обеспечат совместность системы при добавлении фиктивных переменных.

Важно помнить, что неправильно заданные фиктивные переменные могут привести к неверному решению системы уравнений. Поэтому следует внимательно следить за всеми условиями, указанными выше, и правильно выбирать фиктивные переменные для получения корректного решения системы.

Какие ошибки можно допустить при использовании

Использование фиктивных переменных может привести к ошибкам в работе алгоритмов, особенно при неправильном определении предиката. Например, если в предикате происходит сравнение фиктивной переменной с каким-либо значением, это может приводить к неправильной интерпретации результата.

Еще одной распространенной ошибкой является неправильное определение домена фиктивной переменной. Если домен неправильно определен, это может привести к ошибочным результатам или даже повреждению данных. Например, если фиктивная переменная определена в некорректном диапазоне значений, это может привести к некорректному сравнению и дальнейшей обработке данных.

Также следует учитывать, что фиктивная переменная может только заменять недостающие значения, но не добавлять новые. Если фиктивная переменная используется для получения новых данных, это может привести к искажениям результатов и неправильной интерпретации данных.

Наконец, следует помнить, что использование фиктивных переменных может значительно усложнить алгоритмы и делать их труднопонятными и трудночитаемыми. Поэтому необходимо аккуратно оценивать необходимость использования фиктивных переменных и аргументировать свой выбор.

Какие альтернативы существуют для фиктивных переменных

Фиктивные переменные — это удобный и широко используемый инструмент в дискретной математике, но существуют и альтернативные способы решения задач, где фиктивные переменные могут оказаться неэффективными или непригодными.

Один из таких способов – это использование дополнительного ограничения, которое позволяет исключить ненужные варианты решений. Например, в задачах на логические выражения можно использовать законы де Моргана и упрощать выражения без использования фиктивных переменных.

Еще одним альтернативным методом для решения задач без фиктивных переменных является метод муравьиной колонии. Он применяется для решения задач на поиск кратчайшего пути в графе или на оптимизацию планирования производства.

Также можно воспользоваться методом решения линейных уравнений, который позволяет решать системы уравнений методом Гаусса. В результате в уравнения вместо фиктивных переменных будут подставлены найденные значения.

Итак, существует множество альтернативных методов для решения задач, но в некоторых случаях фиктивные переменные все же могут быть наилучшим решением. Однако, при выборе способа решения задачи всегда необходимо учитывать ее условия и особенности.

Какие ограничения бывают при использовании фиктивных переменных

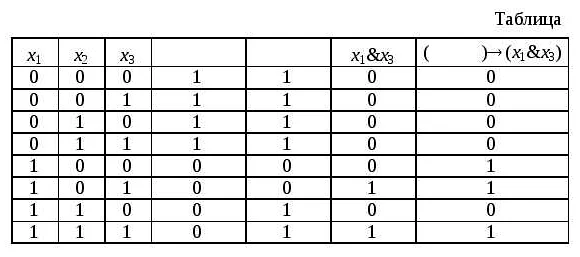
Фиктивные переменные — это простой и популярный способ работы с категориальными переменными в дискретной математике. Однако, при использовании фиктивных переменных, есть несколько ограничений, которые необходимо учитывать.

1. Количество фиктивных переменных: при создании фиктивных переменных для категориальной переменной с k уникальными значениями, необходимо создать k-1 фиктивную переменную. Если создать k фиктивных переменных, то это приведет к проблеме мультиколлинеарности.
2. Значения фиктивных переменных: значение фиктивных переменных должно быть логически последовательными по отношению к заданной категориальной переменной. Если значения фиктивных переменных выбраны неправильно, то это может привести к некорректным результатам.
3. Интерпретация результата: при использовании фиктивных переменных, необходимо правильно интерпретировать результат. В частности, для каждой категориальной переменной можно выбрать только одну фиктивную переменную в качестве базовой. Результаты для других фиктивных переменных должны интерпретироваться относительно базовой фиктивной переменной.

В целом, фиктивные переменные являются важным инструментом в дискретной математике и могут использоваться для работы с категориальными переменными. Однако, для получения корректных результатов необходимо учитывать вышеописанные ограничения.

Какие особенности и выгоды есть при работе с фиктивными переменными

Фиктивные переменные являются важным инструментом в дискретной математике, который позволяет решать множество задач в более компактной и эффективной форме. Ниже приведены основные преимущества и особенности работы с фиктивными переменными.

1. Упрощение логических выражений.

Фиктивные переменные позволяют упростить логические выражения и уменьшить количество логических операций, что в свою очередь увеличивает скорость вычислений и уменьшает вероятность ошибок.

2. Создание более эффективных алгоритмов.

Фиктивные переменные могут использоваться для оптимизации алгоритмов и повышения их эффективности. Например, в алгоритмах поиска пути в графах фиктивные переменные могут использоваться для хранения информации о том, был ли уже пройден конкретный узел.

3. Упрощение задачи логического вывода.

Фиктивные переменные могут использоваться для упрощения задачи логического вывода. Например, в задачах оказания медицинской помощи фиктивные переменные могут использоваться для определения, какие лекарства были приняты, а какие нет, и какие лекарства противопоказаны при определенных заболеваниях.

4. Улучшение читаемости кода.

Использование фиктивных переменных может повысить читаемость кода, благодаря более простой структуре логических выражений и более понятному коду. Это может быть особенно важно в больших проектах, где понимание кода другими разработчиками является критически важным элементом.

5. Создание более гибких и масштабируемых приложений.

Использование фиктивных переменных может сделать приложения более гибкими и масштабируемыми. Например, фиктивные переменные могут использоваться для хранения информации о типе пользовательской учетной записи, позволяя приложению легко изменять права доступа в зависимости от типа учетной записи.

Использование фиктивных переменных может быть очень полезным инструментом для решения сложных задач в дискретной математике. Знание особенностей и преимуществ использования фиктивных переменных позволит вам создавать более эффективные и качественные программы и алгоритмы.

Как дополнительно улучшить использование фиктивных переменных

Фиктивные переменные или «dummy variables» широко используются в дискретной математике для решения проблем, связанных с категориальными данными. Они позволяют «закодировать» категории в бинарные значения, что позволяет проводить статистические анализы на равных условиях с числовыми данными.

Для того, чтобы еще лучше использовать фиктивные переменные, рекомендуется:

• Выбирать правильное количество фиктивных переменных: необходимо добавлять дополнительные фиктивные переменные только тогда, когда это необходимо для того, чтобы избежать ловушек, таких как мультиколлинеарность. При этом не стоит создавать слишком много фиктивных переменных, так как это может привести к переобучению модели и усложнению интерпретации результатов.
• Выбирать правильную фиктивную переменную для группы: если одна категория из нескольких должна быть базовой, то необходимо выбрать для неё соответствующую фиктивную переменную. Это позволит избежать излишнего замусоривания данных и упростит интерпретацию результатов.
• Проводить несколько сравнений: при использовании фиктивных переменных для анализа данных с категориальными переменными может быть полезно провести несколько сравнений, чтобы убедиться, что результаты верны. Это также позволит проверить, какие категории или факторы оказывают существенное влияние на результаты.