Что такое положительные числа в математике

Положительные числа — это числа, которые больше нуля. В математике они используются для представления количества, размера или величины, которые имеют положительное значение. Узнайте больше о положительных числах и их свойствах в математике.

Положительные числа — это числа, которые больше нуля. Они являются одной из основных категорий чисел в математике и имеют ряд важных свойств и характеристик.

Одно из главных свойств положительных чисел заключается в том, что они могут быть складываться, вычитаться, умножаться и делиться между собой. Это формирует основу для выполнения арифметических операций и решения математических задач.

Положительные числа также обладают свойством упорядоченности. Это означает, что их можно расположить на числовой прямой в порядке возрастания. Например, число 1 будет меньше числа 2, а число 5 будет больше числа 3.

Кроме того, положительные числа играют важную роль в различных областях науки и ежедневной жизни. Они используются для измерения количества, определения положительного направления, а также в финансовых и экономических расчетах.

Положительные числа в математике: определение и свойства

Основные свойства положительных чисел:

1. Сложение: Если к положительному числу прибавить другое положительное число, то результат будет положительным числом. Например, 5 + 3 = 8.
2. Вычитание: Если из положительного числа вычесть другое положительное число, то результат также будет положительным числом. Например, 10 — 2 = 8.
3. Умножение: Положительное число, умноженное на положительное число, дает положительный результат. Например, 4 * 2 = 8.
4. Деление: Если положительное число разделить на положительное число, то результат будет положительным числом. Например, 16 / 2 = 8.
5. Возведение в степень: Положительное число, возведенное в положительную степень, дает положительный результат. Например, 23 = 8.

Также положительные числа обладают свойством порядка: если положительные числа сравниваются, то большим будет число, которое находится дальше от нуля на числовой оси. Например, 8 > 5.

Положительные числа играют важную роль в математике и находят применение в различных областях, таких как физика, экономика, геометрия и т. д. Они позволяют осуществлять измерения, моделировать процессы и решать задачи, связанные с количеством, временем, пространством и многими другими величинами.

Что такое положительные числа?

Положительные числа имеют несколько основных свойств:

• Они могут быть целыми числами (1, 2, 3 и так далее), десятичными числами (1.5, 2.75 и т.д.) или дробями (1/2, 3/4 и т.д.).
• Положительные числа можно складывать, вычитать, умножать и делить.
• Если положительное число умножается на положительное число, то результат будет положительным числом.
• Если положительное число делится на положительное число, то результат также будет положительным числом.

Например, если мы сложим два положительных числа, например 3 и 5, получим результат 8. Если умножим 3 на 5, получим 15. Таким образом, положительные числа играют важную роль в математике и используются во многих областях, таких как физика, экономика и т.д.

Определение положительных чисел

Положительные числа имеют ряд свойств:

• Они больше нуля: положительные числа находятся справа от нуля на числовой прямой.
• Они обратны к отрицательным числам: положительные числа и отрицательные числа образуют противоположные пары. Сумма положительного числа и его отрицательного обратного равна нулю.
• Они могут быть целыми или дробными: положительные числа могут быть как целыми, так и дробными.
• Они могут быть представлены в различных системах счисления: положительные числа могут быть представлены в двоичной, восьмеричной, десятичной и других системах счисления.

Положительные числа играют важную роль в математике и имеют широкое применение в различных областях, таких как физика, экономика, статистика и др.

Свойства положительных чисел

СвойствоОписание

Сложение	Положительные числа можно складывать между собой. Результатом сложения двух положительных чисел всегда будет положительное число.
Умножение	Положительные числа можно перемножать. Результатом умножения двух положительных чисел всегда будет положительное число.
Деление	Положительное число можно поделить на положительное число. Результатом деления положительного числа на положительное число будет положительное число.
Степень	Положительное число можно возвести в положительную степень. Результатом возведения положительного числа в положительную степень будет положительное число.
Сравнение	Положительные числа можно сравнивать между собой. Если положительное число A больше положительного числа B, то A > B.

Свойства положительных чисел позволяют проводить различные операции с этими числами и устанавливать отношения между ними.

Как определить положительное число?

• Проверка знака числа: Положительные числа имеют положительный знак «+» перед числом. Если число имеет «+» знак, это означает, что оно является положительным числом.
• Сравнение с нулем: Если число больше нуля, то оно является положительным числом. Например, число 5 больше нуля, поэтому оно положительное.

Также стоит отметить, что в математике существуют отрицательные числа, которые находятся слева от нуля на числовой оси. Они имеют отрицательный знак «-» перед числом.

Знание, как определить положительное число, играет важную роль в различных областях математики, физики, экономики и других наук, где требуется анализ и работа с числами.

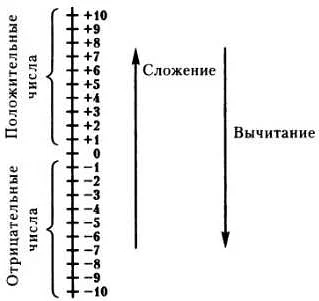
Положительные числа в математических операциях

Положительные числа в математике играют важную роль в различных математических операциях. Они могут быть сложены, вычтены, умножены или разделены друг на друга.

Сложение положительных чисел приводит к увеличению их значения. Например, если мы сложим числа 5 и 3, получим результат 8. Также можно сложить больше двух чисел, при этом сумма будет равна сумме всех слагаемых.

Вычитание положительных чисел приводит к уменьшению значения. Например, если мы вычтем из числа 7 число 4, получим результат 3. Также можно вычесть из числа одно или несколько чисел и получить разность.

Умножение положительных чисел приводит к увеличению значения. Например, если мы умножим число 2 на число 5, получим результат 10. Также можно умножить больше двух чисел, при этом произведение будет равно произведению всех множителей.

Деление положительных чисел приводит к уменьшению значения. Например, если мы разделим число 10 на число 2, получим результат 5. Также можно разделить число на одно или несколько чисел и получить частное.

Помимо основных математических операций, положительные числа могут быть использованы в более сложных операциях, таких как возведение в степень, извлечение корня и другие.

ОперацияПримерРезультат

Сложение	5 + 3	8
Вычитание	7 — 4	3
Умножение	2 * 5	10
Деление	10 / 2	5

Положительные числа на числовой оси

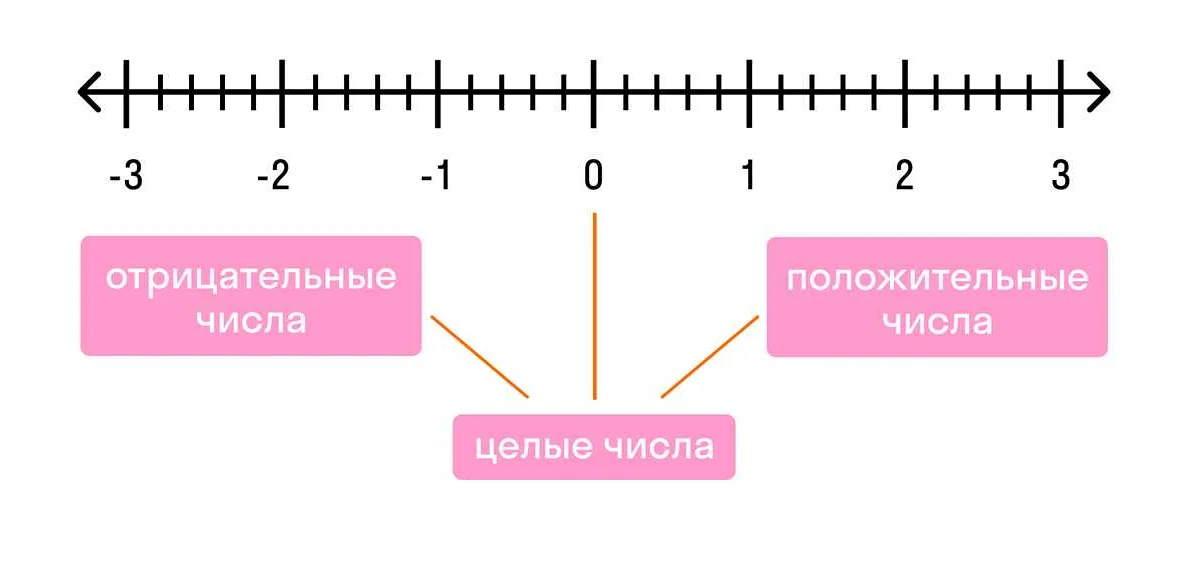
Ноль, обозначаемый символом 0, является точкой отсчета на числовой оси. Влево от нуля располагаются все отрицательные числа, а вправо от нуля – положительные числа.

Положительные числа на числовой оси характеризуются следующими свойствами:

• Они больше нуля.
• Между двумя любыми положительными числами находится бесконечное количество других положительных чисел.
• Чем дальше от нуля, тем больше значение положительного числа.

На числовой оси положительные числа обозначаются точками, которые располагаются справа от нуля. Чем больше значение числа, тем дальше его точка от нулевой точки на числовой оси.

Видео по теме:

Вопрос-ответ:

Что такое положительные числа в математике?

Положительные числа в математике — это числа, которые больше нуля. Они обозначаются положительным знаком (+) перед числом.

Какие свойства имеют положительные числа?

Положительные числа обладают несколькими свойствами. Они могут быть сложены, вычтены, умножены и поделены друг на друга. Также положительные числа могут быть возвышены в степень и извлечены корень. Они также участвуют в различных математических операциях, таких как сравнение и упорядочение чисел.

Какие числа могут считаться положительными?

Положительными могут быть как натуральные числа (1, 2, 3 и так далее), так и целые числа (включая ноль). Все числа, которые больше нуля, считаются положительными.

Как положительные числа используются в реальной жизни?

Положительные числа используются в реальной жизни для представления количества, размеров, значений и многих других величин. Они помогают нам измерять и описывать мир вокруг нас. Например, положительные числа используются для измерения времени, дистанции, скорости, температуры и т.д. Они также используются в финансовых расчетах, науке, инженерии и многих других областях жизни.

Значение положительных чисел в реальном мире

Положительные числа имеют широкое применение в реальном мире и играют важную роль во многих аспектах нашей жизни. Они помогают нам измерять и описывать различные физические величины, количества и характеристики.

Например, положительные числа используются для измерения времени, длины, массы, температуры и скорости. Они позволяют нам определить пройденное расстояние, продолжительность событий и другие параметры, которые являются неотъемлемой частью нашей повседневной жизни.

Положительные числа также находят применение в финансовой сфере. Они помогают нам вести учет доходов и расходов, оценивать прибыль и убытки, а также определять стоимость товаров и услуг.

Кроме того, положительные числа используются для оценки роста и развития. Например, они помогают нам измерять рост растений и животных, а также определять изменения в населении и экономике.

В области науки и техники положительные числа играют важную роль при моделировании процессов, проведении экспериментов и анализе данных. Они помогают нам определить закономерности, прогнозировать результаты и принимать решения на основе полученных данных.

Таким образом, положительные числа имеют большое значение в реальном мире и являются неотъемлемой частью нашей жизни. Они позволяют нам измерять, описывать и анализировать различные явления и процессы, а также принимать решения на основе полученных данных.

Примеры положительных чисел

Например:

• 1 — это наименьшее положительное число. Оно больше нуля, но меньше любого другого положительного числа.
• 2, 3, 4, 5 и так далее — это положительные целые числа.
• 1.5, 2.7, 3.14 и другие десятичные числа больше нуля также являются положительными числами.
• Числа вида a/b, где a и b — положительные числа, а b не равно нулю, также являются положительными числами. Например, 3/4 или 7/8.

Все эти числа являются примерами положительных чисел в математике. Они имеют ряд свойств и используются для решения различных задач и проблем в науке, технике и других областях.