Что называется процентом 6 класс математика
Содержимое
- 1 Что называется процентом 6 класс математика
- 1.1 Что такое процент?
- 1.2 Определение процента
- 1.3 Процент как доля
- 1.4 Процент как отношение
- 1.5 Процент как коэффициент
- 1.6 Примеры задач по математике для 6 класса
- 1.7 Решение задач с процентами
- 1.8 Задачи на нахождение процентов
- 1.9 Задачи на нахождение доли
- 1.10 Вопрос-ответ:
- 1.10.0.1 Что такое процент?
- 1.10.0.2 Как вычислить процент от числа?
- 1.10.0.3 Как решить задачу на нахождение процента?
- 1.10.0.4 Как решить задачу на нахождение числа, если известен процент?
- 1.10.0.5 Можно ли найти число, если известна его часть в процентах?
- 1.10.0.6 Что такое процент?
- 1.10.0.7 Как решать задачи по процентам в 6 классе?
- 1.11 Видео по теме:
Процент в математике для 6 класса – это способ представления доли числа в процентном выражении. В данной статье рассмотрены основные понятия и правила работы с процентами в 6 классе математики.
Процент — это такая математическая величина, которая показывает часть от целого. Он обозначается символом % и используется во множестве сфер нашей жизни. Знание процентов и умение выполнять с ними различные операции является важной компетенцией в современном мире.
Проценты широко используются в финансовой сфере, при расчете налогов, в процессе торговли, при изучении статистики и в других областях. Умение считать проценты помогает нам понимать, как изменяются значения при увеличении или уменьшении на определенный процент.
Например, если товар стоит 100 рублей, а его цена увеличивается на 10%, то новая цена будет равна 110 рублям. В этом примере, 10% — это процент, который показывает на сколько увеличилась цена товара.
Умение решать задачи с процентами — это один из важных навыков, которые изучаются в школе. В этой статье мы рассмотрим несколько примеров задач по математике с процентами, которые подходят для учеников 6 класса. Задачи помогут развить навыки анализа, логического мышления и умение применять математические операции на практике.
Что такое процент?

Проценты используются для удобства в расчетах и позволяют сравнивать разные величины на основе их отношения друг к другу. Например, проценты используются для расчета налогов, скидок, процентных ставок по кредитам и вкладам.
Проценты могут быть представлены в виде десятичной дроби или десятичной дроби с процентным символом. Например, 50% можно представить как 0,5 или как 50/100.
Когда говорят о процентах, часто упоминают базу и процентную ставку. База – это величина, к которой относятся проценты. Процентная ставка – это процент, который берется от базы.
Для вычисления процента от базы используется формула:
Процент = (База × Процентная ставка) / 100
Например, если база равна 100 и процентная ставка равна 10%, то процент будет равен (100 × 10) / 100 = 10.
И наоборот, для вычисления базы по известному проценту и процентной ставке используется формула:
База = (Процент × 100) / Процентная ставка
Например, если процент равен 10 и процентная ставка равна 10%, то база будет равна (10 × 100) / 10 = 100.
Знание процентов и умение работать с ними очень полезно в повседневной жизни. Они помогают проводить различные расчеты, сравнивать цены и скидки, а также понимать финансовые операции.
Определение процента
Процентное значение показывает, сколько частей из 100 составляет данное число или количество. Например, если 70% — это 70 из 100, то это значит, что данное число составляет 70% от всего.
Процент также может быть положительным или отрицательным. Положительный процент указывает на прирост или увеличение, а отрицательный процент указывает на убыль или уменьшение.
Проценты широко используются в различных областях, таких как финансы, экономика, статистика и торговля. Знание процентов позволяет легче сравнивать и анализировать данные, делать финансовые прогнозы и планировать бюджет.
Процент как доля
Проценты широко используются в различных сферах жизни. Например, при расчете скидок и наценок, распределении голосов на выборах, вычислении процентной ставки по кредитам или депозитам и т. д. Понимание процента и умение работать с ним является важным навыком в математике и повседневной жизни.
Процент как отношение

Процент выражается в виде числа, которое указывает, сколько процентов составляет одна величина от другой. Например, если мы говорим, что 50% от 200 равно 100, это означает, что половина от 200 равна 100.
Процент обозначается символом «%», который ставится после числа. Например, 50% читается как «50 процентов».
Проценты могут быть использованы для решения различных задач. Например, мы можем использовать проценты для вычисления скидки на товар, нахождения процента от числа или для вычисления изменения величины в процентах.
Чтобы решить задачу на проценты, нужно уметь правильно выражать отношение в процентах и правильно использовать формулы для решения задач.
Процент как коэффициент
Для вычисления процента от числа используется следующая формула:
Процент = (Число * Коэффициент) / 100
Например, если нужно найти 20% от числа 100, то:
ЧислоКоэффициентПроцент
| 100 | 0.2 | (100 * 0.2) / 100 = 20 |
Таким образом, 20% от числа 100 равно 20.
Проценты широко используются в различных сферах, например, в финансах, в расчетах налогов, в торговле. Понимание процентов поможет вам лучше ориентироваться во многих ситуациях и сделать правильный выбор.
Примеры задач по математике для 6 класса

1. В магазине было 150 книг. 30% книг продались. Сколько книг осталось в магазине?
2. Цена велосипеда составляет 5000 рублей. Каждый год цена велосипеда увеличивается на 8%. Какая будет цена велосипеда через 3 года?
3. Длина отрезка составляет 15 см. Найдите 20% от этой длины.
4. В школе 500 учеников. 45% учеников занимаются спортом. Сколько учеников занимаются спортом в школе?
5. В аптеке было 120 пачек лекарства. 60% пачек лекарства продано. Сколько пачек лекарства осталось в аптеке?
6. Стоимость компьютера составляет 20000 рублей. Каждый год стоимость компьютера уменьшается на 10%. Какая будет стоимость компьютера через 5 лет?
7. В библиотеке было 2500 книг. 15% книг выставили на выставку. Сколько книг осталось в библиотеке?
8. В классе 30 учеников. 20% учеников занимаются футболом. Сколько учеников занимаются футболом в классе?
9. Цена билета в кино составляет 300 рублей. Каждый год цена билета увеличивается на 5%. Какая будет цена билета через 4 года?
10. Длина отрезка составляет 12 см. Найдите 30% от этой длины.
Решение задач с процентами
Для решения задач с процентами нужно уметь использовать формулу процента:
Часть = Процент * Целое / 100
Рассмотрим примеры задач:
Пример 1:
Какой процент составляет 25 из 100?
Для решения данной задачи нужно использовать формулу процента. В данном случае, Целое равно 100, а Часть – 25.
Процент = 25 * 100 / 100 = 25%
Ответ: 25%.
Пример 2:
Стоимость товара увеличилась с 200 рублей до 250 рублей. Найдите процент увеличения стоимости.
Для решения данной задачи нужно найти разницу между новой и старой стоимостью, а затем использовать формулу процента.
Разница = Новая стоимость – Старая стоимость = 250 – 200 = 50 рублей
Процент = 50 * 100 / 200 = 25%
Ответ: 25%.
Пример 3:
Петя правильно решил 12 из 15 задач. Найдите процент правильно решенных задач.
Для решения данной задачи нужно использовать формулу процента. В данном случае, Целое равно 15, а Часть – 12.
Процент = 12 * 100 / 15 = 80%
Ответ: 80%.
Решая задачи с процентами, необходимо внимательно анализировать условие и правильно применять формулу процента. Постепенно, с решением задач, навыки работы с процентами будут улучшаться и станут более легкими.
Задачи на нахождение процентов

Проценты широко используются в повседневной жизни, поэтому умение решать задачи на их нахождение является важным навыком. В таких задачах часто требуется найти процент от числа, найти число, если известен процент от него, или найти процентный прирост или убыль относительно изначального значения.
Вот несколько примеров задач на нахождение процентов:
Пример 1:
В магазине проводится скидка 20% на все товары. Сколько стоит товар, если его изначальная цена была 1000 рублей?
Решение: Чтобы найти стоимость товара со скидкой, нужно умножить его изначальную цену на (100% — процент скидки). В данном случае процент скидки составляет 20%, то есть 0,2 в десятичной форме. Поэтому стоимость товара со скидкой будет равна 1000 * (1 — 0,2) = 800 рублей.
Пример 2:
Зарплата работника увеличилась на 15%. Сколько работник зарабатывает теперь, если его изначальная зарплата составляла 50000 рублей?
Решение: Чтобы найти новую зарплату работника, нужно прибавить к его изначальной зарплате процентный прирост. В данном случае процентный прирост составляет 15%, то есть 0,15 в десятичной форме. Поэтому новая зарплата работника будет равна 50000 + (50000 * 0,15) = 57500 рублей.
Таким образом, задачи на нахождение процентов помогают ученикам развить навыки работы с процентами и научиться применять полученные знания на практике. Решение таких задач требует умения преобразовывать проценты в десятичную форму и применять соответствующие математические операции.
Задачи на нахождение доли
Решение задач на нахождение доли требует знания процентов и умения применять их в практических ситуациях. Долей называется часть от целого, которую необходимо найти в процентах.
Ниже представлены примеры задач, в которых необходимо найти долю:
- В магазине на распродаже скидка составляет 20%. Сколько стоит товар, если его исходная цена была 5000 рублей?
- В классе 30 учеников, из которых 60% это девочки. Сколько девочек в классе?
- В городе проживает 5000 человек, из которых мужчин 40%. Сколько мужчин проживает в городе?
Для решения задач на нахождение доли необходимо использовать формулу:
Доля = (Процент / 100) * Целое
где:
- Доля — искомая величина;
- Процент — известное значение процента;
- Целое — значение от которого находим долю.
Применяя данную формулу к приведённым выше задачам, можно получить следующие ответы:
- Скидка на товар составляет 1000 рублей;
- В классе 18 девочек;
- В городе проживает 2000 мужчин.
Таким образом, решение задач на нахождение доли позволяет определить искомую часть от целого в процентном выражении.
Вопрос-ответ:
Что такое процент?
Процент – это доля от целого, выраженная в сотых долях.
Как вычислить процент от числа?
Процент от числа можно найти, умножив число на процент и разделив полученное значение на 100.
Как решить задачу на нахождение процента?
Чтобы решить задачу на нахождение процента, нужно умножить число на процент и разделить полученное значение на 100.
Как решить задачу на нахождение числа, если известен процент?
Чтобы решить задачу на нахождение числа, если известен процент, нужно умножить процент на 100 и поделить на значение процента.
Можно ли найти число, если известна его часть в процентах?
Да, можно найти число, если известна его часть в процентах. Для этого нужно умножить процент на 100 и разделить на значение процента.
Что такое процент?
Процент — это доля чего-либо от 100. Он позволяет выразить одну величину относительно другой и удобен в использовании для сравнения и анализа данных.
Как решать задачи по процентам в 6 классе?
В 6 классе задачи по процентам обычно сводятся к нахождению процента от числа, нахождению числа, если известен процент от него, или нахождению процентной ставки. Для решения таких задач необходимо уметь работать с пропорциями и основными формулами для вычисления процента.


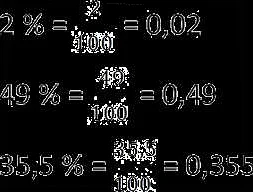


Статья очень понятно и доступно объясняет, что такое проценты. Мне было интересно узнать, как применять это понятие на практике. Примеры задач помогли мне лучше понять, как решать математические задачи, связанные с процентами. Теперь я знаю, что проценты используются в различных ситуациях, например, при расчете скидок или процентного увеличения. Статья очень полезна для шестиклассников, так как помогает закрепить знания и научиться применять их на практике. Я рекомендую эту статью всем, кто хочет лучше понять и освоить математику.