Произведение чисел это что в математике 3

Произведение чисел – это важное понятие в математике, которое означает умножение двух или более чисел. Узнайте, как вычислять произведение чисел и как оно используется в различных математических операциях.

Произведение чисел — одна из основных операций в математике, которая позволяет найти результат умножения двух или более чисел. Эта операция широко используется в различных областях науки, техники и повседневной жизни.

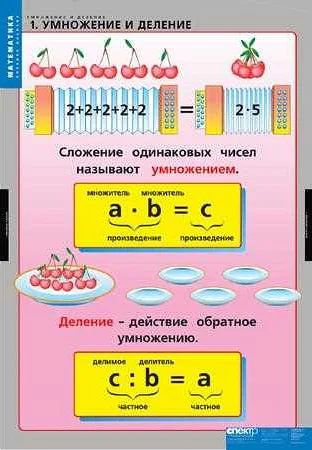
Произведение чисел обозначается символом «×» или «*», и записывается в виде выражения, где числа, подлежащие умножению, разделяются этим символом. Например, произведение чисел 4 и 5 будет выглядеть следующим образом: 4 × 5 = 20.

Вычисление произведения чисел сводится к последовательному сложению одного числа определенное количество раз. Например, чтобы найти произведение чисел 4 и 5, нужно сложить число 4 пять раз: 4 + 4 + 4 + 4 + 4 = 20. Данный способ вычисления произведения называется «повторное сложение».

Операция умножения обладает несколькими свойствами, которые позволяют упростить вычисления. Например, произведение числа на 1 равно самому числу, а произведение числа на 0 равно нулю. Кроме того, порядок перемножения чисел не влияет на результат, что позволяет менять их местами без изменения результата.

Определение произведения чисел

Произведение чисел обозначается символом умножения (×). Например, произведение чисел 3 и 4 будет записываться как 3 × 4.

При умножении двух чисел, первое число называется множимым, а второе число — множителем. Ответ, полученный в результате умножения, называется произведением этих чисел.

Произведение чисел можно вычислить с помощью таблицы умножения, где каждая ячейка содержит результат умножения двух чисел. Например, для вычисления произведения чисел 3 и 4, можно найти в таблице значение, соответствующее пересечению строки номер 3 и столбца номер 4.

Произведение чисел также можно вычислить с помощью умножения в столбик или с использованием калькулятора.

Какое значение имеет произведение чисел в математике

Математическое обозначение для произведения чисел выглядит следующим образом: a * b = c, где a и b — множители, а c — произведение. Множитель a может быть любым числом, включая дроби и отрицательные числа.

Произведение чисел позволяет решать задачи, связанные с умножением, распределением, нахождением площади и объема, а также моделированием процессов. Например, в физике произведение силы и расстояния используется для вычисления момента силы.

Кроме того, произведение чисел имеет свойства, которые позволяют упростить вычисления. Например, ассоциативное свойство позволяет изменять порядок множителей без изменения результата: (a * b) * c = a * (b * c). Коммутативное свойство позволяет менять местами множители: a * b = b * a.

Таким образом, произведение чисел играет важную роль в математике и науке, обеспечивая возможность проведения различных вычислений и моделирования реальных ситуаций.

Произведение чисел: основные свойства и определения

Определение произведения чисел:

Для любых двух чисел a и b их произведением называется число c, такое что a · b = c. Произведение чисел является результатом сложения a, сколько раз, равное b.

Например, если a = 3 и b = 4, то их произведение будет равно 3 · 4 = 12.

Основные свойства произведения чисел:

1. Коммутативность: Порядок сомножителей не влияет на результат произведения. То есть a · b = b · a.

2. Ассоциативность: Результат произведения не зависит от того, какая пара чисел будет сначала перемножена. То есть (a · b) · c = a · (b · c).

3. Дистрибутивность: Произведение числа на сумму равно сумме произведений этого числа на каждое слагаемое. То есть a · (b + c) = (a · b) + (a · c).

Знание основных свойств и определений произведения чисел позволяет эффективно решать задачи и использовать его в различных областях математики и её приложений.

Как вычислить произведение двух чисел

Для примера, рассмотрим два числа: 4 и 7. Чтобы вычислить их произведение, нужно умножить 4 на 7:

4 * 7 = 28

Таким образом, произведение чисел 4 и 7 равно 28.

При вычислении произведения двух чисел необходимо помнить об основных свойствах операции умножения:

1. Коммутативность: порядок умножения не влияет на результат. Например, 4 * 7 = 7 * 4.
2. Ассоциативность: результат умножения не зависит от расстановки скобок. Например, (4 * 7) * 3 = 4 * (7 * 3).
3. Свойство нейтрального элемента: умножение числа на 1 дает тоже число. Например, 4 * 1 = 4.
4. Свойство нулевого элемента: умножение числа на 0 дает 0. Например, 4 * 0 = 0.
5. Распределительное свойство: умножение числа на сумму дает равную сумму умножений. Например, 4 * (7 + 3) = (4 * 7) + (4 * 3).

Используя эти свойства, можно упростить вычисление произведения чисел и сделать его более эффективным.

Теперь вы знаете, как вычислить произведение двух чисел и какие свойства операции умножения помогают упростить это вычисление.

Методы вычисления произведения нескольких чисел

В математике произведение нескольких чисел представляет собой результат умножения этих чисел между собой. Существует несколько методов вычисления произведения чисел, которые могут быть использованы в различных ситуациях.

Один из наиболее простых способов вычисления произведения нескольких чисел — это последовательное умножение. Для этого необходимо взять первое число и последовательно умножить его на каждое из остальных чисел. Этот метод прост и понятен, однако может быть неэффективен при большом количестве чисел, так как требует много операций умножения.

Еще одним методом вычисления произведения чисел является использование свойств ассоциативности и коммутативности умножения. Суть этого метода заключается в группировке чисел и последовательном вычислении произведений групп. Например, можно сгруппировать числа попарно и вычислить произведения пар, а затем перемножить полученные произведения. Этот метод может быть более эффективным при большом количестве чисел, так как требует меньше операций умножения.

Также существуют специальные алгоритмы для вычисления произведения больших чисел, которые не могут быть представлены стандартными типами данных. Эти алгоритмы основаны на использовании различных приемов, таких как деление числа на блоки и последовательное умножение блоков чисел. Такие алгоритмы могут быть сложными в реализации, но позволяют вычислять произведение чисел произвольной длины.

В зависимости от конкретной задачи и доступных ресурсов, можно выбирать наиболее подходящий метод вычисления произведения чисел. Важно учитывать как точность результата, так и время, затрачиваемое на вычисления.

Произведение чисел в различных системах счисления

Произведение чисел в математике представляет собой операцию, при которой два или более числа комбинируются для получения их общего умножения.

Одно из интересных аспектов произведения чисел заключается в том, что оно может быть выполнено не только в десятичной системе счисления, но и в других системах счисления, таких как двоичная, восьмеричная и шестнадцатеричная.

В двоичной системе счисления произведение двух чисел аналогично умножению в десятичной системе, но используются только две цифры — 0 и 1. Например, произведение чисел 101 и 110 в двоичной системе равно 11110.

В восьмеричной системе счисления произведение чисел также выполняется по тем же правилам, что и в десятичной системе, но используются восемь цифр — от 0 до 7. Например, произведение чисел 53 и 26 в восьмеричной системе равно 1362.

В шестнадцатеричной системе счисления произведение чисел также выполняется по тем же правилам, что и в десятичной системе, но используются шестнадцать цифр — от 0 до 9 и от A до F. Например, произведение чисел 4A и 2F в шестнадцатеричной системе равно 157A.

Произведение чисел в различных системах счисления является важной математической операцией, которая находит применение как в теории, так и в практических задачах. Понимание процесса произведения чисел в различных системах счисления помогает углубить знания в области математики и применять их в реальных ситуациях.

Практическое применение произведения чисел

Одним из примеров применения произведения чисел является вычисление площади прямоугольника. Площадь прямоугольника можно найти умножив длину его стороны на ширину. Например, если длина прямоугольника равна 5 см, а ширина – 3 см, то его площадь будет равна 15 квадратных сантиметров (5 * 3 = 15).

Другим примером практического применения произведения чисел является вычисление стоимости товаров. Если стоимость одной единицы товара равна 10 долларам, а необходимо купить 5 единиц, то общая стоимость будет равна 50 долларам (10 * 5 = 50).

Также произведение чисел используется в физике для вычисления работы и энергии. Например, работа, совершенная телом, равна произведению силы, приложенной к телу, на расстояние, на которое это тело перемещается. Если сила равна 10 Н (Ньютон), а расстояние – 5 м (метров), то работа будет равна 50 Дж (Джоулей) (10 * 5 = 50).

Таким образом, произведение чисел имеет широкое практическое применение в различных сферах, от геометрии и экономики до физики. Оно позволяет нам находить результаты умножения чисел и применять их в реальных ситуациях.

Примеры решения задач на произведение чисел

Пример 1: Вася купил 3 яблока по 25 рублей каждое. Сколько рублей он потратил на яблоки?

Решение:

Для вычисления общей стоимости яблок, нужно умножить количество яблок на цену одного яблока.

Общая стоимость яблок = 3 * 25 = 75 рублей.

Пример 2: У Маши было 10 карандашей, она отдала половину своих карандашей своему другу. Сколько карандашей осталось у Маши?

Решение:

Для вычисления количества оставшихся карандашей, нужно от общего количества карандашей вычесть количество отданных карандашей.

Количество оставшихся карандашей = 10 — (10 / 2) = 10 — 5 = 5 карандашей.

Пример 3: Сколько весит 5 ящиков, если каждый ящик весит 20 кг?

Решение:

Для вычисления общего веса ящиков, нужно умножить вес одного ящика на количество ящиков.

Общий вес ящиков = 5 * 20 = 100 кг.

Результаты и обсуждение

Умножение в столбик является основным методом вычисления произведения двух чисел. Оно основано на принципе поэлементного умножения цифр чисел, а затем суммирования полученных произведений. Данный метод хорошо подходит для вычисления произведения чисел любой длины.

Таблица умножения также может быть использована для вычисления произведения чисел. В таблице умножения представлены все возможные комбинации перемножения чисел от 1 до 10. Для вычисления произведения двух чисел нужно найти соответствующую ячейку в таблице и прочитать значение, которое находится в этой ячейке.

Калькулятор является самым простым способом вычисления произведения чисел. Для этого достаточно ввести числа и нажать кнопку «Умножить». Калькулятор автоматически выполнит операцию умножения и выдаст результат.

Выбор метода вычисления произведения чисел зависит от конкретной задачи и предпочтений человека. Каждый метод имеет свои преимущества и недостатки. Например, умножение в столбик является более трудоемким, но позволяет вычислить произведение чисел любой длины, в то время как использование калькулятора быстро и просто, но может быть ограничено количеством разрядов чисел.

В итоге, произведение чисел является важной операцией в математике, которая широко применяется в различных областях. Понимание основных методов вычисления произведения позволяет более эффективно выполнять математические операции и решать задачи.

Вопрос-ответ:

Какое определение произведения чисел в математике?

Произведение чисел — это операция, которая позволяет узнать результат умножения двух или более чисел.

Как вычислить произведение двух чисел?

Для вычисления произведения двух чисел необходимо умножить первое число на второе число.

А что делать, если нужно вычислить произведение более чем двух чисел?

Если необходимо вычислить произведение более чем двух чисел, то нужно последовательно умножать каждое число на следующее.

Какое значение имеет произведение числа на ноль?

Произведение числа на ноль всегда равно нулю. Независимо от значения числа, если умножить его на ноль, результат будет равен нулю.

Можно ли производить операции с произведением чисел, если они содержат десятичную часть?

Да, можно. Десятичные числа также могут участвовать в операции произведения. Для этого необходимо умножить их, как и обычные числа, но учесть их десятичную часть в конечном результате.

Видео по теме: