Что такое компонент умножения в математике

Компонент умножения в математике — это один из множителей, используемых для выполнения операции умножения. Узнайте, как определить компонент умножения и как использовать его в математических выражениях.

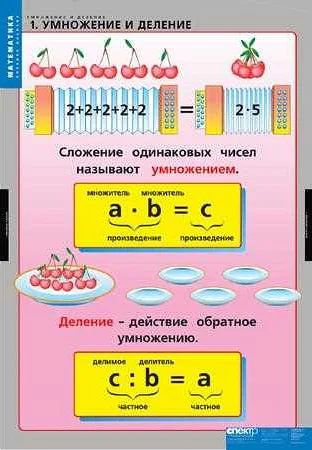
Компонент умножения — это математическое понятие, которое относится к операции умножения чисел. Умножение является одной из основных арифметических операций, которая позволяет получить произведение двух или более чисел. В контексте компонента умножения, числа, участвующие в операции, называются множителями. Результат умножения называется произведением. Компонент умножения играет важную роль в различных областях науки и техники, а также в повседневной жизни.

Операция умножения имеет свои особенности, которые помогают лучше понять компонент умножения. Например, умножение является коммутативной операцией, что означает, что порядок множителей не влияет на результат. Также умножение обладает свойством дистрибутивности, которое позволяет раскрывать скобки при умножении чисел.

Примеры компонента умножения могут быть найдены во многих сферах нашей жизни. Например, при покупке продуктов в магазине, мы можем вычислить общую стоимость, умножив цену одного товара на его количество. В инженерии, умножение используется для расчета мощности электрической схемы. В физике, умножение используется для вычисления силы, площади и других физических величин. Компонент умножения является неотъемлемой частью нашей повседневной жизни и научных исследований.

Что такое компонент умножения?

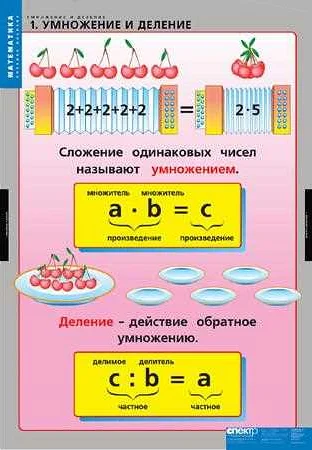
Когда мы умножаем два числа, одно из них называется первым сомножителем, а другое — вторым сомножителем. В результате умножения мы получаем произведение этих двух чисел. Таким образом, каждое из чисел в умножении называется компонентом этого умножения.

Например, в умножении 4 * 5 = 20, число 4 является первым сомножителем, а число 5 — вторым сомножителем. Таким образом, компонентами этого умножения являются числа 4 и 5.

Компоненты умножения могут быть любыми числами, включая целые числа, десятичные дроби и отрицательные числа. Умножение является одной из основных арифметических операций и используется в различных ситуациях, от решения математических задач до выполнения повседневных расчетов.

Видео по теме:

Определение компонента умножения

В умножении есть два компонента: множимое и множитель. Множимое — это число, которое увеличивается, а множитель — это число, на которое увеличивается множимое. Результатом умножения является произведение, которое получается путем сложения множимого само с собой столько раз, сколько указано в множителе.

Например, если множимое равно 4, а множитель равен 5, то результатом умножения будет 20. Это означает, что число 4 увеличивается 5 раз и получается число 20.

Компоненты умножения могут быть любыми числами, как положительными, так и отрицательными. При умножении двух отрицательных чисел результатом будет положительное число.

Таблица ниже показывает примеры компонентов умножения:

МножимоеМножитель

2	3
5	4
-3	6
-4	-2

Как определить компонент умножения?

Компонент умножения может быть представлен в виде отдельного числа или переменной. В умножении, компоненты умножения располагаются слева направо и разделяются знаком умножения (*).

Например, в умножении 2 * 3 = 6, число 2 и число 3 являются компонентами умножения. В этом примере число 2 — первый компонент умножения, а число 3 — второй компонент умножения.

Компоненты умножения могут быть как целыми числами, так и десятичными числами. Они могут быть положительными или отрицательными. Также компоненты умножения могут быть представлены в виде переменных, которые могут принимать различные значения.

Умножение применяется не только в математике, но и в других областях, таких как физика, экономика, программирование и т.д. Знание и понимание компонентов умножения является важным для решения различных задач и проблем.

Вопрос-ответ:

Что такое компонент умножения?

Компонент умножения — это один из элементов, присутствующих в уравнении умножения. Он является одним из множителей, которые участвуют в умножении и определяют произведение.

Какие примеры можно привести для компонента умножения?

Примерами компонентов умножения могут быть числа, переменные, выражения или даже функции. Например, в уравнении 2 * 3 = 6, числа 2 и 3 являются компонентами умножения.

Как определить компонент умножения в сложном математическом выражении?

Для определения компонента умножения в сложном математическом выражении, необходимо найти все множители, которые присутствуют в умножении. Это могут быть числа, переменные или выражения, разделенные знаком умножения.

Может ли компонент умножения быть отрицательным числом?

Да, компонент умножения может быть как положительным, так и отрицательным числом. Знак умножения задает только операцию умножения, но не влияет на знак компонента.

Могут ли компоненты умножения быть дробями или десятичными числами?

Да, компоненты умножения могут быть как дробями, так и десятичными числами. В умножении можно использовать любые числа, которые можно умножать между собой.

Что такое компонент умножения?

Компонент умножения — это элементарная операция, которая производит умножение двух чисел. Он представляет собой одну из основных операций арифметики и используется для решения различных задач и вычислений.

Примеры компонента умножения

Ниже приведены несколько примеров компонента умножения:

1. Умножение двух чисел: 5 * 3 = 15
2. Умножение трех чисел: 2 * 4 * 6 = 48
3. Умножение числа на ноль: 8 * 0 = 0
4. Умножение отрицательных чисел: -3 * -4 = 12
5. Умножение числа на единицу: 7 * 1 = 7

Компонент умножения широко используется в математике, физике, экономике и других науках. Он позволяет умножать числа, чтобы получить результат, который может быть использован для решения различных задач и проблем.

Примеры использования компонента умножения

ПримерРезультат

4 * 5	20
8 * 2	16
12 * 3	36
7 * 9	63

Это лишь небольшой набор примеров использования компонента умножения. В реальной жизни его можно применять для решения различных задач, таких как определение стоимости товаров, вычисление площади или объема объектов, анализ данных и многое другое.

Компонент умножения является одной из основных операций в математике и является фундаментальным для понимания более сложных математических концепций. Поэтому важно уметь правильно использовать этот компонент в различных контекстах и задачах.

Практическое применение компонента умножения

• Финансовая аналитика: в бухгалтерии и финансовой сфере используется умножение для расчета различных финансовых показателей, таких как прибыль, стоимость активов и рентабельность.
• Программирование: умножение используется в программировании для выполнения различных математических операций, например, для вычисления значений функций или масштабирования данных.
• Научные исследования: в научных исследованиях умножение применяется для анализа и обработки данных, создания моделей и прогнозирования результатов.
• Инженерия: в инженерных расчетах умножение используется для определения различных параметров, таких как сила, давление, скорость и энергия.
• Статистика: в статистическом анализе умножение применяется для вычисления различных статистических показателей, таких как среднее значение, дисперсия и корреляция.

Это лишь некоторые примеры практического применения компонента умножения. Он широко используется в различных областях науки, техники, экономики и других сферах деятельности, где требуется выполнение математических операций для анализа данных и принятия решений.

Как применить компонент умножения в реальной жизни?

Ниже приведены несколько примеров, показывающих, как компонент умножения может быть использован в повседневной жизни:

1. Покупки в магазине: Когда мы покупаем товары в магазине, мы часто сталкиваемся с необходимостью умножать цену товара на его количество, чтобы получить общую стоимость покупки.
2. Кулинария: При приготовлении еды, особенно при изменении пропорций рецепта, необходимо умножать ингредиенты на определенный коэффициент, чтобы подготовить нужное количество блюда.
3. Расчеты времени и скорости: В жизни мы часто сталкиваемся с необходимостью умножать скорость на время, чтобы определить расстояние, пройденное за определенный период времени или время, затраченное на преодоление определенного расстояния.
4. Финансы: Умножение используется в финансовых расчетах, таких как расчет процентов по кредиту или инвестициям, расчет доходности инвестиций и других финансовых операций.

Это лишь несколько примеров использования компонента умножения в реальной жизни. Однако, в мире существует бесконечное количество ситуаций, где умножение играет важную роль в решении задач и принятии решений.

Выводы о компоненте умножения

Умножение имеет свои особенности и правила, которые следует учитывать при проведении операции. Например, результат умножения чисел не зависит от порядка их расположения, то есть умножение коммутативно.

Компонент умножения широко применяется в различных областях науки и техники. Он является основой для решения множества задач и применяется в алгебре, геометрии, физике, экономике и других научных дисциплинах.

Примерами использования компонента умножения могут быть вычисление площади прямоугольника, нахождение общего количества предметов при заданной стоимости и единичной цене, определение производительности системы и т. д.

В заключение, компонент умножения является важной математической операцией, которая находит широкое применение в научных и практических областях. Правильное использование и понимание этой операции позволяет проводить разнообразные вычисления и решать задачи различной сложности.