Что такое произведение в математике и частное

Произведение — это одна из основных операций в математике, которая выполняется путем умножения двух или более чисел. Частное — это результат операции деления, где одно число делится на другое. Узнайте больше о произведении и частном в математике и их свойствах.

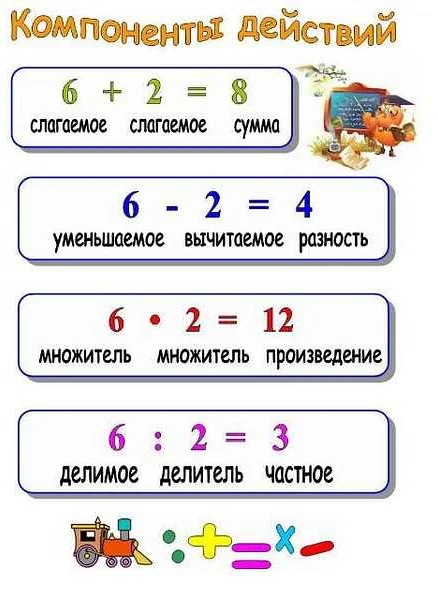
Произведение и частное являются двумя основными операциями в математике.

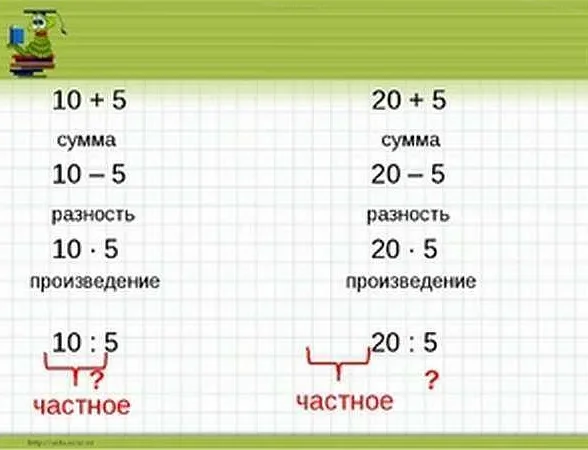
Произведение — это результат умножения двух или более чисел. Оно обозначается знаком умножения «×» или точкой «.». Например, произведение двух чисел 2 и 3 равно 6 (2 × 3 = 6). Можно также умножать более чем два числа, результат будет получен перемножением всех этих чисел. Например, произведение чисел 2, 3 и 4 равно 24 (2 × 3 × 4 = 24).

Частное — это результат деления одного числа на другое. Оно обозначается символом деления «÷» или косой чертой «/». Например, частное чисел 6 и 2 равно 3 (6 ÷ 2 = 3). Частное может быть как целым числом, так и десятичной дробью. Например, частное чисел 7 и 2 равно 3.5 (7 ÷ 2 = 3.5).

Произведение и частное имеют множество применений в математике и в повседневной жизни. Произведение может использоваться для вычисления площади прямоугольника или объема параллелепипеда, а частное — для определения среднего значения или расчета скорости.

Понятие произведения в математике

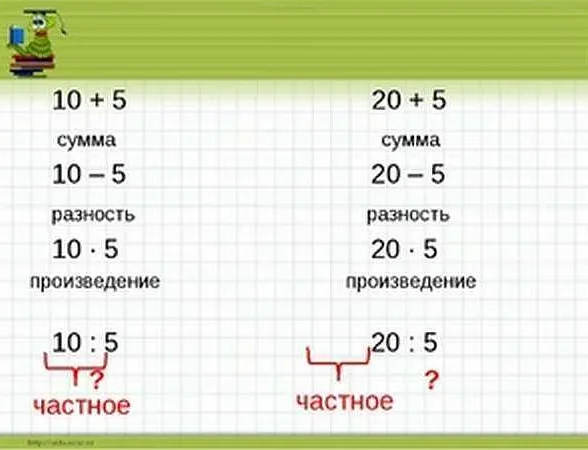
Произведение обозначается знаком умножения «×» или точкой «.». Например, произведение двух чисел 3 и 4 записывается как 3 × 4 или 3 · 4, и равно 12.

Для удобства вычислений произведение не зависит от порядка множителей. Это свойство называется коммутативностью произведения. Например, произведение 2 × 5 равно 10, и это же произведение можно записать как 5 × 2, получив тот же результат.

Произведение также обладает свойством ассоциативности, то есть можно изменять порядок скобок. Например, произведение 2 × (3 × 4) равно 2 × 12, и это же произведение можно записать как (2 × 3) × 4, получив тот же результат.

Произведение играет важную роль в различных областях математики, таких как алгебра, геометрия, анализ и теория вероятностей. Оно используется для решения уравнений, вычисления площадей и объемов, моделирования случайных событий и многих других задач.

Определение и основные свойства

Частное — это операция, которая выполняется над двумя числами и позволяет найти результат деления одного числа на другое. Частное чисел a и b обозначается как a / b или a : b.

Операции произведения и частного имеют некоторые основные свойства:

1. Ассоциативность: Порядок выполнения операций произведения и частного не влияет на результат. Например: (a * b) * c = a * (b * c) и (a / b) / c = a / (b / c).
2. Коммутативность: Порядок чисел не влияет на результат операции произведения. Например: a * b = b * a. Однако коммутативность не выполняется для операции частного: a / b ≠ b / a.
3. Распределительное свойство: Произведение двух чисел, а затем результат умножения умножается на третье число, равно произведению каждого числа, умноженного на третье число. Например: a * (b + c) = (a * b) + (a * c).
4. Единица и ноль: Умножение числа на единицу не меняет значение этого числа. Например: a * 1 = a. Деление числа на единицу также не меняет значения числа: a / 1 = a. Умножение числа на ноль всегда дает ноль: a * 0 = 0. Однако деление нуля на любое число невозможно.
5. Обратный элемент: Для каждого числа a существует обратный элемент, такой что a * (1/a) = 1. Однако обратного элемента для операции частного может не существовать.

Знание определения и основных свойств произведения и частного в математике позволяет эффективно выполнять операции с числами и использовать их в различных математических задачах и формулах.

Примеры вычисления произведения

Пример 1:

Вычислим произведение чисел 5 и 7.

Произведение равно 5 * 7 = 35.

Пример 2:

Рассмотрим произведение трех чисел: 2, 3 и 4.

Произведение равно 2 * 3 * 4 = 24.

Пример 3:

Для примера возьмем произведение чисел 10 и 0.

Произведение равно 10 * 0 = 0.

Пример 4:

Посчитаем произведение чисел 1, 2, 3, 4 и 5.

Произведение равно 1 * 2 * 3 * 4 * 5 = 120.

Таким образом, произведение – это результат умножения чисел и может быть вычислено для любого количества чисел.

Понятие частного в математике

Частное обозначается символом «÷» или «/». Чтобы найти частное двух чисел, нужно первое число разделить на второе.

Например, если у нас есть числа 10 и 2, то частное будет равно 5, так как 10 ÷ 2 = 5.

В математике также существует понятие «деление с остатком», когда результатом деления является не только частное, но и остаток.

Например, если мы разделим число 10 на 3, то получим частное 3 и остаток 1, так как 10 ÷ 3 = 3, остаток 1.

Частное может быть положительным, отрицательным или нулем, в зависимости от знаков исходных чисел.

Знание понятия частного в математике позволяет решать различные задачи, такие как расчеты, деление предметов на группы и другие.

Определение и применение

Произведение может быть применено для вычисления площади прямоугольника или для определения количества объектов в группе. Например, если у нас есть 4 группы по 5 человек в каждой, мы можем найти общее количество людей, умножив 4 на 5, что даст нам 20.

Частное также имеет множество применений в реальной жизни. Например, если у нас есть 10 яблок и мы хотим разделить их поровну между 2 детьми, мы можем использовать операцию деления для определения, сколько яблок получит каждый ребенок. В этом случае, частное будет равно 5 яблок для каждого ребенка.

Операции произведения и частного также широко используются в алгебре, где они применяются для решения уравнений и нахождения неизвестных переменных. Например, мы можем использовать произведение для раскрытия скобок в алгебраических выражениях или частное для нахождения значения неизвестной переменной в уравнении.

ОперацияПримерРезультат

Произведение	3 * 4	12
Частное	10 / 2	5

Основные свойства частного

• Свойство ассоциативности: порядок скобок при делении не влияет на результат. Например, если a, b и c – любые числа, то (a ÷ b) ÷ c = a ÷ (b ÷ c).
• Свойство коммутативности: порядок чисел при делении не влияет на результат. Например, если a и b – любые числа, то a ÷ b = b ÷ a.
• Свойство нуля: частное нуля и любого числа равно нулю. Например, 0 ÷ a = 0.
• Свойство единицы: частное любого числа и единицы равно самому числу. Например, a ÷ 1 = a.
• Свойство сокращения: если числитель и знаменатель частного можно разделить на одно и то же число, то частное не изменится. Например, если a и b – любые числа, то (2a ÷ 2b) = (a ÷ b).

Основные свойства частного помогают упростить выражения и решить задачи, используя простые математические операции деления.

Произведение и частное в арифметике

Произведение обозначается символом «×» или «*», и записывается как:

Число AЧисло BПроизведение

2

3

6

Например, произведение чисел 2 и 3 равно 6.

Частное обозначается символом «÷» или «/», и записывается как:

Число AЧисло BЧастное

6

2

3

Например, частное чисел 6 и 2 равно 3.

Произведение и частное являются важными операциями в математике и используются в различных областях, таких как физика, экономика, инженерия и т. д.

Произведение и частное целых чисел

Произведение и частное целых чисел представляют собой основные арифметические операции, которые выполняются над числами.

Произведение двух целых чисел определяется как результат умножения этих чисел. Например, произведение чисел 3 и 4 равно 12, так как 3 * 4 = 12.

Частное двух целых чисел определяется как результат деления одного числа на другое. Например, частное чисел 12 и 3 равно 4, так как 12 / 3 = 4.

Оба этих понятия имеют важное значение в математике и широко применяются в решении различных задач.

Видео по теме:

Вопрос-ответ:

Что такое произведение в математике?

Произведение — это результат умножения двух или более чисел. В математике произведение обозначается символом «×» или «.»

Как вычислить произведение двух чисел?

Для вычисления произведения двух чисел нужно умножить эти числа. Например, произведение чисел 2 и 3 равно 6 (2 × 3 = 6).

Можно ли умножать больше двух чисел?

Да, конечно. В математике можно умножать любое количество чисел. Например, произведение чисел 2, 3 и 4 равно 24 (2 × 3 × 4 = 24).

Что такое частное в математике?

Частное — это результат деления одного числа на другое. В математике обозначается символом «÷» или «/».

Как вычислить частное двух чисел?

Для вычисления частного двух чисел нужно разделить одно число на другое. Например, частное чисел 6 и 2 равно 3 (6 ÷ 2 = 3).

Что такое произведение в математике?

Произведение в математике — это операция умножения двух или более чисел. Результатом произведения является число, полученное путем умножения всех чисел вместе.

Произведение и частное десятичных дробей

Например:

0.5 * 0.2 = 0.1

1.25 * 0.8 = 1.0

Частное десятичных дробей – это операция, при которой десятичная дробь делится на другую десятичную дробь. Частное двух десятичных дробей находится путем деления числителя первой дроби на числитель второй дроби и знаменателя первой дроби на знаменатель второй дроби.

Например:

0.6 / 0.3 = 2.0

1.5 / 0.5 = 3.0

При умножении или делении десятичных дробей, результатом всегда будет десятичная дробь. Ответ можно округлить до определенного количества знаков после запятой, чтобы получить более удобный и точный результат.

Произведение и частное смешанных чисел

Произведение смешанных чисел находится путем умножения целой части каждого числа и сложения с произведением дробных частей. Например, чтобы найти произведение $2 \frac{1}{2}$ и $3 \frac{3}{4}$, нужно выполнить следующие действия:

1. Умножить целую часть каждого числа: $2 \cdot 3 = 6$
2. Найти произведение дробных частей: $\frac{1}{2} \cdot \frac{3}{4} = \frac{3}{8}$
3. Сложить результаты: $6 + \frac{3}{8} = 6 \frac{3}{8}$

Таким образом, произведение $2 \frac{1}{2}$ и $3 \frac{3}{4}$ равно $6 \frac{3}{8}$.

Частное смешанных чисел находится путем деления числителя на знаменатель. Например, чтобы найти частное $5 \frac{2}{3}$ и $1 \frac{1}{4}$, нужно выполнить следующие действия:

1. Перевести смешанные числа в неправильные дроби: $5 \frac{2}{3} = \frac{17}{3}$ и $1 \frac{1}{4} = \frac{5}{4}$
2. Выполнить деление числителя на знаменатель: $\frac{17}{3} \div \frac{5}{4} = \frac{68}{15}$

Таким образом, частное $5 \frac{2}{3}$ и $1 \frac{1}{4}$ равно $\frac{68}{15}$.