Что такое признаки делимости в математике

Признаки делимости в математике — это определенные правила и свойства, которые позволяют определить, делится ли одно число на другое без остатка. В этой статье рассматриваются основные признаки делимости, такие как признаки делимости на 2, 3, 4, 5, 6, 9 и 10, а также методы проверки чисел на делимость. Узнайте, как использовать эти признаки для упрощения решения математических задач и определения свойств чисел.

Математика – это наука, которая изучает числа и их взаимоотношения. Одним из важных понятий в математике является делимость. Делимость – это свойство чисел, при котором одно число делится на другое без остатка. В данной статье мы рассмотрим основные правила и признаки делимости, которые помогут упростить работу с числами и выполнение различных задач.

Основными правилами делимости являются правила делимости на 2, 3, 4, 5, 6, 8, 9 и 10. Правило делимости на 2 гласит, что если число заканчивается на четную цифру (0, 2, 4, 6, 8), то оно делится на 2 без остатка. Например, число 24 делится на 2, так как оно заканчивается на цифру 4. Правило делимости на 3 утверждает, что число делится на 3 без остатка, если сумма его цифр также делится на 3. Например, число 123 делится на 3, так как сумма его цифр равна 6, которая также делится на 3.

Правило делимости на 4 гласит, что число делится на 4 без остатка, если две последние цифры числа образуют число, которое делится на 4. Например, число 148 делится на 4, так как число 48 делится на 4.

Правило делимости на 5 утверждает, что число делится на 5 без остатка, если его последняя цифра является 0 или 5. Например, число 125 делится на 5, так как его последняя цифра – 5. Правило делимости на 6 утверждает, что число делится на 6 без остатка, если оно делится как на 2, так и на 3. Например, число 72 делится на 6, так как оно делится на 2 (последняя цифра – 2) и на 3 (сумма цифр равна 9, которая делится на 3).

Правило делимости на 8 гласит, что число делится на 8 без остатка, если тре последние цифры числа образуют число, которое делится на 8. Например, число 4568 делится на 8, так как число 568 делится на 8. Правило делимости на 9 утверждает, что число делится на 9 без остатка, если сумма его цифр также делится на 9. Например, число 153 делится на 9, так как сумма его цифр равна 9, которая также делится на 9.

Правило делимости на 10 гласит, что число делится на 10 без остатка, если его последняя цифра является 0. Например, число 320 делится на 10, так как его последняя цифра – 0.

Основные понятия

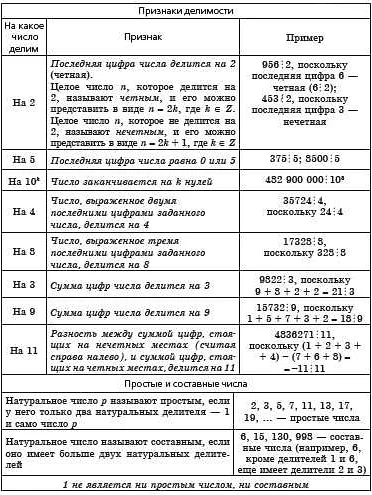
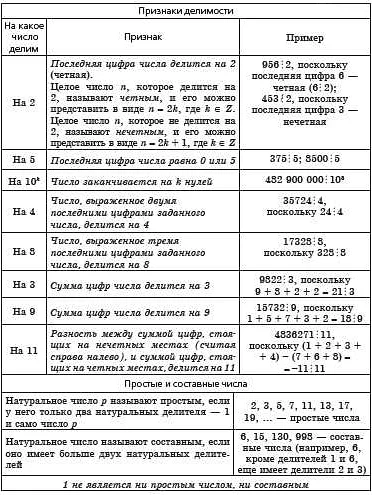
Основные правила делимости включают:

• Правило делимости на 2: число делится на 2, если его последняя цифра четная (0, 2, 4, 6, 8).
• Правило делимости на 3: число делится на 3, если сумма его цифр также делится на 3.
• Правило делимости на 5: число делится на 5, если его последняя цифра 0 или 5.
• Правило делимости на 9: число делится на 9, если сумма его цифр также делится на 9.

Делимость имеет много применений в различных областях математики, включая алгебру, комбинаторику и теорию чисел. Понимание основных понятий и правил делимости позволяет решать сложные задачи и строить более глубокие математические модели.

Видео по теме:

Правило делимости на 2

Например, рассмотрим число 2468. Последняя цифра этого числа — 8, и она является четной. Следовательно, число 2468 делится на 2.

Если же последняя цифра числа не является четной, то число не делится на 2. Например, число 1357. Последняя цифра этого числа — 7, и она не является четной. Следовательно, число 1357 не делится на 2.

Правило делимости на 2 очень простое и удобное в использовании. Оно позволяет быстро определить, делится ли число на 2 или нет.

ЧислоПоследняя цифраДелится на 2?

2468	8	Да
1357	7	Нет

Правило делимости на 3

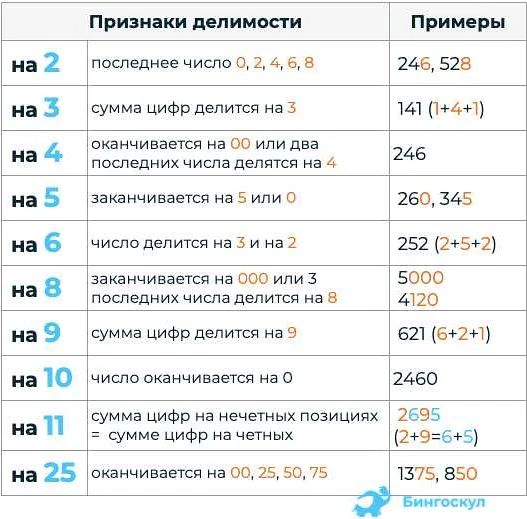
Рассмотрим примеры:

ЧислоСумма цифрДелимость на 3

6	6	Да
12	1 + 2 = 3	Да
27	2 + 7 = 9	Да
45	4 + 5 = 9	Да
50	5 + 0 = 5	Нет

Таким образом, если сумма цифр числа кратна 3, то само число также будет делиться на 3 без остатка.

Вопрос-ответ:

Что такое признак делимости числа на 2?

Признак делимости на 2 гласит, что число делится на 2, если его последняя цифра четная. Например, число 36 делится на 2, потому что его последняя цифра 6 — четная.

Какой признак делимости числа на 3?

Признак делимости на 3 гласит, что число делится на 3, если сумма его цифр также делится на 3. Например, число 123 делится на 3, потому что 1 + 2 + 3 = 6, и 6 делится на 3.

Как определить, делится ли число на 5?

Число делится на 5, если его последняя цифра является 0 или 5. Например, числа 30 и 45 делятся на 5, так как их последние цифры 0 и 5 соответственно.

Какой признак делимости числа на 9?

Признак делимости на 9 гласит, что число делится на 9, если сумма его цифр также делится на 9. Например, число 135 делится на 9, потому что 1 + 3 + 5 = 9, и 9 делится на 9.

Что такое признак делимости числа на 10?

Признак делимости на 10 гласит, что число делится на 10, если его последняя цифра равна 0. Например, число 50 делится на 10, потому что его последняя цифра 0.

Что такое признаки делимости в математике?

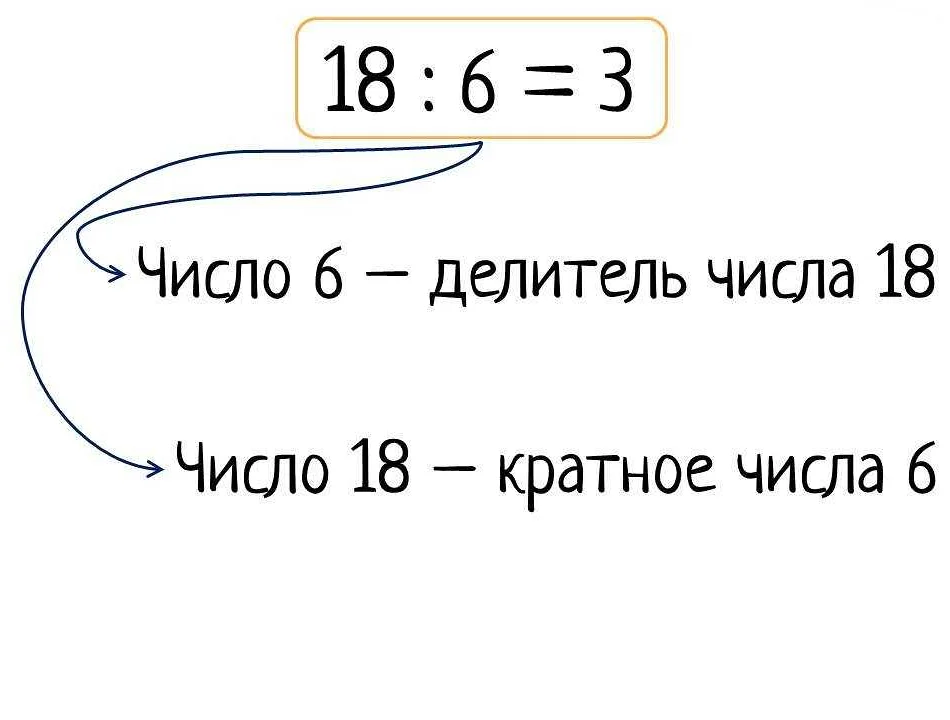
Признаки делимости в математике — это правила и свойства, которые позволяют определить, делится ли одно число на другое без остатка. Они помогают нам узнать, является ли число кратным или делителем другого числа.

Какие основные правила признаков делимости существуют?

В математике существуют несколько основных правил признаков делимости. Некоторые из них:

Правило делимости на 4

Примеры:

• Число 132: последние две цифры 32, которые делятся на 4 без остатка. Следовательно, число 132 делится на 4.
• Число 247: последние две цифры 47, которые не делятся на 4 без остатка. Следовательно, число 247 не делится на 4.

Используя правило делимости на 4, можно легко определить, является ли число кратным 4 или нет.

Правило делимости на 5

Например, число 25 делится на 5, потому что его последняя цифра — 5. А число 30 также делится на 5, так как его последняя цифра — 0.

Используя правило делимости на 5, можно с легкостью определить, делится ли некоторое число на 5, просто посмотрев на его последнюю цифру.

Если число заканчивается на 0 или 5, то оно делится на 5 без остатка. В противном случае, оно не делится на 5.

Например, число 123 не делится на 5, так как его последняя цифра не является ни 0, ни 5.

Правило делимости на 5 может быть использовано в решении различных задач, связанных с делимостью чисел и нахождением кратных чисел.

ЧислоДелится на 5?

15	Да
28	Нет
45	Да
50	Да

Примеры делимости

1. Делимость на 2: если число делится на 2 без остатка, то оно является четным числом. Например, число 4 является четным, так как оно делится на 2 без остатка.

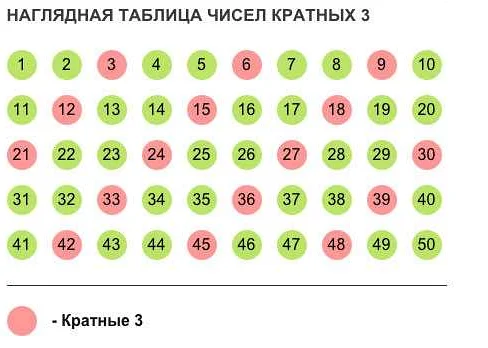
2. Делимость на 3: если сумма цифр числа делится на 3 без остатка, то число также делится на 3. Например, число 123 делится на 3, так как 1 + 2 + 3 = 6, а 6 делится на 3 без остатка.

3. Делимость на 5: если число заканчивается на 0 или 5, то оно делится на 5 без остатка. Например, число 35 делится на 5, так как оно заканчивается на 5.

4. Делимость на 9: если сумма цифр числа делится на 9 без остатка, то число также делится на 9. Например, число 108 делится на 9, так как 1 + 0 + 8 = 9, а 9 делится на 9 без остатка.

Это лишь несколько примеров делимости, и существует множество других правил и условий, которые могут быть использованы для определения делимости чисел. Понимание этих примеров и правил поможет вам в решении математических задач и применении математики в повседневной жизни.