Что такое произведение в математике 2 класс правило

Произведение в математике для учащихся 2 класса — это результат умножения двух чисел. Ученикам объясняют правило умножения и демонстрируют его на конкретных примерах. Изучение произведения помогает развить навыки умножения и понять его принципы.

Произведение — одна из основных операций в математике, которая используется для умножения чисел. Во втором классе ученики начинают изучать это понятие и осваивать правила умножения. Произведение позволяет находить результат умножения двух или более чисел.

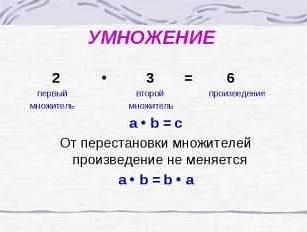
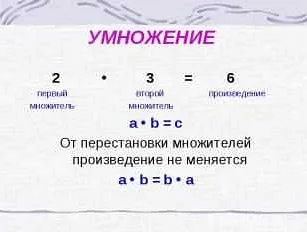
Основные понятия, связанные с произведением, включают множители и произведение. Множители — это числа, которые участвуют в операции умножения. Произведение — это результат умножения множителей. Например, в уравнении 2 * 3 = 6, числа 2 и 3 являются множителями, а число 6 — произведением.

Важно понимать, что порядок множителей в произведении не влияет на результат. Например, в уравнении 3 * 2 = 6, результат будет таким же, как и в предыдущем примере, потому что умножение — коммутативная операция.

Для упрощения вычислений с произведением второклассники используют правила умножения. Одним из таких правил является правило умножения на 1. Суть этого правила заключается в том, что если число умножить на 1, то результатом будет само это число. Например, 5 * 1 = 5.

Другим важным правилом умножения второго класса является правило умножения на 0. По этому правилу, если число умножить на 0, то результатом всегда будет 0. Например, 7 * 0 = 0.

Определение произведения

Для умножения чисел используется знак умножения (×). Например, для умножения числа 3 на число 4 записывается как 3 × 4.

Произведение двух чисел можно представить как сумму одного числа, взятого нужное количество раз. Например, произведение 3 × 4 равно сумме чисел 3 + 3 + 3 + 3, что равно 12.

Правило умножения гласит, что произведение чисел не зависит от порядка их умножения. Например, произведение 3 × 4 равно произведению 4 × 3, и в обоих случаях результат будет равен 12.

Произведение можно найти не только для целых чисел, но и для дробей, десятичных чисел и других математических объектов.

Видео по теме:

Основные понятия

Произведение двух чисел можно найти, перемножив эти числа. Например, произведение чисел 3 и 4 равно 12, так как 3 умножить на 4 равно 12.

Когда мы умножаем число на 1, произведение будет равно самому числу. Например, произведение числа 7 и 1 равно 7.

Умножение также обладает свойством коммутативности, что означает, что порядок чисел не влияет на результат умножения. Например, произведение чисел 5 и 2 равно произведению чисел 2 и 5, то есть 10.

В математике используются специальные обозначения для произведения. Знак умножения обозначается символом «×» или «*», например, 3 × 4 или 3 * 4.

Также существуют правила умножения, которые помогают упростить процесс вычисления произведения. Например, произведение числа на 0 всегда будет равно 0, а произведение числа на 10 можно получить, добавив ноль к правому концу числа.

Правила умножения чисел

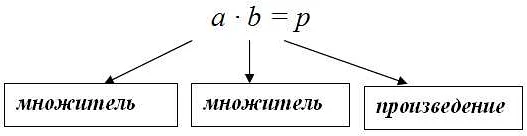
Основные правила умножения:

ПравилоПримерРезультат

Умножение на 0	5 * 0	0
Умножение на 1	7 * 1	7
Умножение на 2	4 * 2	8
Умножение на 10	6 * 10	60

Для умножения числа на 0 результатом всегда будет 0. Если умножить число на 1, результатом будет само число, так как оно не меняется. Умножение на 2 эквивалентно сложению числа с самим собой. Умножение на 10 эквивалентно добавлению нуля в конце числа.

Умножение на ноль

Например:

3 * 0	=	0
-7 * 0	=	0
0,5 * 0	=	0

Умножение на ноль можно представить как умножение числа на ноль единиц. Ноль единиц дает ноль.

Это правило можно применять в различных задачах и вычислениях. Например, если умножить количество яблок на ноль, то получим ноль яблок.

Запомните, что умножение на ноль всегда дает результат ноль.

Умножение на единицу

Умножение на единицу — это особый случай умножения, когда один из множителей равен единице. Если любое число умножить на единицу, то результатом будет то же число.

Например, 5 умножить на 1 равно 5:

5 х 1 = 5

Также, любое число, умноженное на единицу, равно этому числу:

2 х 1 = 2

7 х 1 = 7

10 х 1 = 10

Таким образом, умножение на единицу не меняет значение числа.

Умножение на десятки, сотни и тысячи

Например, если у нас есть число 5, а мы умножим его на 10, получим 50. Умножив число 5 на 100, получим 500. И если умножить число 5 на 1000, получим 5000.

При умножении на десятки, сотни и тысячи, важно помнить, что порядок цифр в числе не меняется. То есть, если у нас есть число 123, а мы умножим его на 10, получим число 1230. Умножение на 100 даст число 12300, а умножение на 1000 – число 123000.

Также важно помнить, что при умножении на десятки, сотни и тысячи, количество нулей в конце числа увеличивается. Например, если у нас есть число 7, а мы умножим его на 10, получим число 70. При умножении на 100 – число 700, а на 1000 – число 7000.

Умножение на десятки, сотни и тысячи – это важное правило в математике, которое помогает упростить вычисления и увеличить числа в разы.

Примеры умножения

Пример 1: 2 × 3 = 6

Для того чтобы найти произведение 2 и 3, нужно умножить первое число (2) на второе число (3). Результатом будет число 6.

Пример 2: 4 × 5 = 20

Умножим число 4 на число 5 и получим произведение, равное 20.

Пример 3: 7 × 2 = 14

При умножении числа 7 на число 2 получаем результат — 14.

Пример 4: 9 × 0 = 0

Умножение числа на ноль всегда дает ноль. Поэтому произведение числа 9 и нуля равно нулю.

Пример 5: 6 × 1 = 6

Умножение числа на единицу не меняет число. Поэтому произведение числа 6 и единицы равно 6.

Это только некоторые примеры умножения. Чтобы получить точный результат, нужно правильно умножать числа в соответствии с правилами умножения.

Вопрос-ответ:

Что такое произведение в математике?

Произведение в математике — это результат умножения двух или более чисел. Например, произведение 2 и 3 равно 6.

Какие правила умножения нужно знать во 2 классе?

Во 2 классе нужно знать основные правила умножения: коммутативное свойство (порядок множителей не влияет на результат), ассоциативное свойство (группировка множителей не влияет на результат), правило умножения на 1 (любое число умноженное на 1 равно этому числу) и правило умножения на 0 (любое число умноженное на 0 равно 0).

Как вычислить произведение двух чисел?

Для вычисления произведения двух чисел нужно перемножить эти числа. Например, чтобы найти произведение 4 и 5, нужно умножить эти числа: 4 * 5 = 20.

Как умножать числа, больше десяти?

Умножение чисел, больших десяти, осуществляется по тем же правилам, что и умножение чисел до десяти. Например, чтобы найти произведение 12 и 6, нужно умножить эти числа: 12 * 6 = 72.

Что будет, если умножить число на ноль?

Если умножить любое число на ноль, получится ноль. Например, 5 * 0 = 0. Это связано с правилом умножения на 0.

Какое правило умножения используется в математике для вычисления произведения?

В математике для вычисления произведения используется правило умножения, которое гласит, что произведение двух чисел можно найти, перемножив эти числа.