Что такое произведение множителей в математике

Произведение множителей в математике — это результат умножения двух или более чисел. Оно позволяет нам находить общее значение для группы чисел и используется в различных математических операциях и задачах. Узнайте, как найти произведение множителей и его свойства.

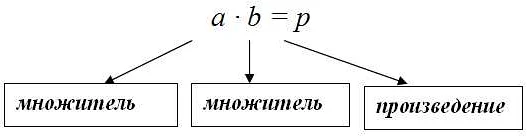
Произведение множителей – одно из основных понятий в математике, которое олицетворяет умножение. Умножение – это операция, в результате которой два или более числа объединяются в одно число, называемое произведением. В математической записи произведение обозначается знаком умножения (×) или точкой (·).

Произведение множителей может быть представлено как умножение чисел, так и умножение алгебраических выражений. В обоих случаях произведение является результатом совместного действия множителей и имеет свои особенности и свойства.

Например, произведение чисел 4 и 5 равно 20, так как 4 × 5 = 20. Это означает, что при совместном перемножении двух чисел, первое число (4) увеличивается в 5 раз, то есть умножается на второе число (5).

Что такое произведение множителей?

Множители – это числа, которые участвуют в операции умножения. В умножении, первое число называется первым множителем, а второе – вторым множителем. Если в умножении участвуют больше двух чисел, они также называются множителями.

Произведение множителей обозначается знаком умножения «×» или точкой «·». Например, произведение множителей 4 и 5 можно записать как 4 × 5 или 4 · 5.

Произведение множителей можно вычислить путем сложения нескольких одинаковых чисел. Например, произведение множителей 3 и 4 равно сумме чисел 3 + 3 + 3 + 3, что равно 12.

Произведение множителей имеет несколько свойств, таких как коммутативность (порядок множителей не влияет на результат), ассоциативность (порядок выполнения умножений не влияет на результат), и дистрибутивность (умножение распределено относительно сложения). Эти свойства помогают в вычислении произведений множителей с большим количеством чисел.

Произведение множителей является важным понятием в математике и находит применение в различных областях, таких как физика, экономика, статистика и других. Знание и понимание этой операции является основой для выполнения более сложных математических операций.

Определение и основные понятия

Произведение обозначается символом «×» или знаком умножения «*». Например, произведение двух чисел a и b записывается как a × b или a * b.

Множители могут быть любыми числами — натуральными, целыми, рациональными или действительными. В зависимости от типа множителей и результата умножения, произведение может принадлежать различным множествам чисел.

Произведение множителей имеет ряд свойств и особенностей. Например, коммутативность — результат умножения не зависит от порядка множителей. Ассоциативность — можно изменять порядок умножения при наличии нескольких множителей. Нейтральный элемент — умножение на единицу не меняет значение числа. Нулевой элемент — умножение на ноль дает всегда ноль. И дистрибутивность — умножение распространяется на сложение и вычитание.

Произведение множителей активно используется в решении математических задач, как в обычной жизни, так и в научных и инженерных областях. Например, при рассчетах стоимости товаров, площади фигур, скорости и т.д.

Таблица ниже приводит примеры произведений множителей:

Множитель 1Множитель 2Произведение

2	3	6
4	5	20
6	2	12

Как вычислить произведение множителей?

Чтобы вычислить произведение множителей, нужно умножить все числа вместе. Если у нас есть только два множителя, то мы умножаем их численное значение. Например, чтобы найти произведение чисел 2 и 3, нужно умножить их вместе: 2 * 3 = 6.

Если у нас есть больше двух множителей, мы умножаем их поочередно. Например, чтобы найти произведение чисел 2, 3 и 4, нужно сначала умножить 2 и 3, а затем полученный результат умножить на 4: (2 * 3) * 4 = 24.

Вычисление произведения множителей может быть полезным при решении различных задач, например, при нахождении площади прямоугольника или объема параллелепипеда.

Также в математике есть свойства произведения множителей, которые могут помочь в вычислениях. Например, свойство коммутативности гласит, что порядок множителей не важен: a * b = b * a. Свойство ассоциативности гласит, что скобки можно расставлять по своему усмотрению: (a * b) * c = a * (b * c).

Примеры вычисления произведения множителей

Пример 1:

Вычислим произведение множителей 4 и 6:

4 × 6 = 24

Таким образом, произведение множителей 4 и 6 равно 24.

Пример 2:

Вычислим произведение множителей 2, 3 и 5:

2 × 3 × 5 = 30

Произведение множителей 2, 3 и 5 равно 30.

Пример 3:

Вычислим произведение множителей 7 и (-3):

7 × (-3) = -21

Произведение множителей 7 и (-3) равно -21.

Это лишь некоторые примеры вычисления произведения множителей. В математике произведение множителей используется для решения широкого спектра задач и применяется во многих областях науки и повседневной жизни.

Зачем нужно знать произведение множителей?

• Произведение множителей позволяет нам умножать большие и/или десятичные числа без использования калькулятора. Это очень полезно, когда нам нужно быстро рассчитать результат или оценить порядок величины числа.
• Знание произведения множителей помогает нам понять и использовать другие математические операции, такие как деление, сложение и вычитание. Во многих случаях при решении задач мы будем использовать несколько операций одновременно, и знание произведения множителей поможет нам учесть все необходимые шаги и правильно выполнить вычисления.
• Произведение множителей является основой для понимания более сложных понятий и операций в математике, таких как алгебраические выражения, уравнения и системы уравнений. Знание произведения множителей позволит нам более глубоко и полно понять и использовать эти концепции и методы.
• Знание произведения множителей также полезно в повседневной жизни. Мы можем использовать его для решения различных задач, связанных с финансами, строительством, торговлей и другими областями, где нам нужно быстро и точно производить вычисления.

Таким образом, знание произведения множителей является неотъемлемой частью математической грамотности и позволяет нам лучше понять и использовать различные математические операции и концепции в повседневной жизни и в других областях нашей деятельности.

Применение произведения множителей в реальной жизни

В финансовой сфере произведение множителей используется, например, для расчета процентной ставки по вкладам или кредитам. Для этого необходимо умножить начальную сумму на процентную ставку и на количество лет, чтобы получить конечную сумму. Это позволяет оценить доходность вклада или расчитать общую сумму выплат по кредиту.

В физике произведение множителей используется для вычисления различных физических величин. Например, для определения работы, сила умножается на расстояние, которое пройдет объект, чтобы получить работу, совершенную над ним. Аналогично, для определения импульса, масса умножается на скорость.

В экономике произведение множителей применяется для расчета стоимости товаров или услуг. Например, для определения общей стоимости товара необходимо умножить его стоимость на количество единиц товара. Это позволяет оценить затраты на производство или приобретение товара.

В технике произведение множителей используется для решения различных инженерных задач. Например, для расчета мощности электрической цепи необходимо умножить напряжение на силу тока. А для определения общего сопротивления цепи, сопротивления каждого элемента цепи умножается друг на друга.

ОбластьПример применения произведения множителей

Финансы	Расчет процентной ставки по вкладу или кредиту
Физика	Определение работы или импульса
Экономика	Расчет общей стоимости товаров или услуг
Техника	Решение инженерных задач, например, расчет мощности или сопротивления

Таким образом, произведение множителей имеет широкое и практическое применение в реальной жизни, позволяя решать различные задачи и вычисления в разных областях.

Вопрос-ответ:

Что такое произведение множителей в математике?

Произведение множителей в математике — это результат умножения двух или более чисел. В умножении числа на число (множителя) получается произведение, которое равно сумме этих чисел, взятых определенное количество раз.

Как вычислить произведение множителей?

Для вычисления произведения множителей необходимо перемножить все числа, которые являются множителями. Например, если есть множители 2, 3 и 4, то произведение будет равно 2*3*4=24.

Какие примеры произведения множителей в математике?

Примерами произведения множителей могут быть умножение чисел, например 3*4=12, или умножение переменных, например a*b=c. Также произведением множителей может быть умножение комплексных чисел или матриц.

Какое свойство имеет произведение множителей?

Произведение множителей обладает свойствами коммутативности и ассоциативности. Свойство коммутативности означает, что порядок умножения множителей не влияет на результат. Свойство ассоциативности означает, что при умножении трех или более чисел порядок их умножения можно менять без изменения результата.

Какое значение имеет произведение множителей в математике?

Значение произведения множителей в математике зависит от значений самих множителей. Например, при умножении положительных чисел произведение будет положительным, а при умножении отрицательных чисел — отрицательным. Также произведение множителей может использоваться для решения уравнений и задач из различных областей науки и техники.

Что такое произведение множителей в математике?

Произведение множителей — это результат умножения двух или более чисел.

Как вычислить произведение множителей?

Для вычисления произведения множителей нужно перемножить все числа, которые являются множителями.

Особенности произведения множителей в математике

Одной из особенностей произведения множителей является коммутативность. Это значит, что порядок расположения множителей не влияет на результат произведения. Например, произведение чисел 2 и 3 будет равно произведению чисел 3 и 2.

Также важно учесть, что произведение двух множителей может быть равно нулю только в случае, если один из множителей равен нулю. Если хотя бы один из множителей равен нулю, то произведение всегда будет равно нулю.

Однако, если все множители являются ненулевыми числами, то произведение всегда будет положительным числом. Если количество множителей четное, то произведение будет положительным. Если количество множителей нечетное, то произведение будет отрицательным.

Произведение множителей также может быть представлено в виде степенной формы, где каждый множитель является основанием степени, а показатель степени равен количеству множителей.

В математике существует ряд специальных свойств произведения множителей, таких как ассоциативность, дистрибутивность и др., которые помогают упростить вычисления и решение математических задач.

Видео по теме: