Правила по математике во сколько раз больше или меньше

Познакомьтесь с правилами умножения и деления на число, во сколько раз больше или меньше. Узнайте, как сравнивать числа и определять их отношение друг к другу с помощью простых математических операций. Полезная информация для всех, кто интересуется математикой и хочет лучше понять численные отношения.

Математика — одна из основных наук, которая изучает числа, их свойства и взаимоотношения. В учебной программе школы, математика занимает одно из важнейших мест, так как она помогает развить логическое мышление и способность решать проблемы.

Одним из ключевых понятий в математике является сравнение чисел. Знание, во сколько раз одно число больше или меньше другого, помогает понять и определить отношения между числами. Это очень полезно в различных ситуациях, например, при сравнении цен на товары, вычислении процентов и многих других задачах.

Чтобы определить, во сколько раз одно число больше или меньше другого, необходимо использовать специальную формулу. Для этого нужно разделить одно число на другое и получить отношение между ними. Если результат больше единицы, это означает, что первое число больше второго. Если результат меньше единицы, то первое число меньше второго. Если результат равен единице, значит числа равны.

Например, если число 8 разделить на 4, получим результат 2. Это означает, что 8 в 2 раза больше 4. Если же число 4 разделить на 8, получим результат 0.5. Это значит, что 4 в 0.5 раза меньше 8.

Знание правил по определению во сколько раз одно число больше или меньше другого является важным элементом в математике. Это помогает не только в ежедневной жизни, но и в решении более сложных задач. Поэтому, важно усвоить эту тему и применять полученные знания в практике.

Правила по математике: определение относительной величины

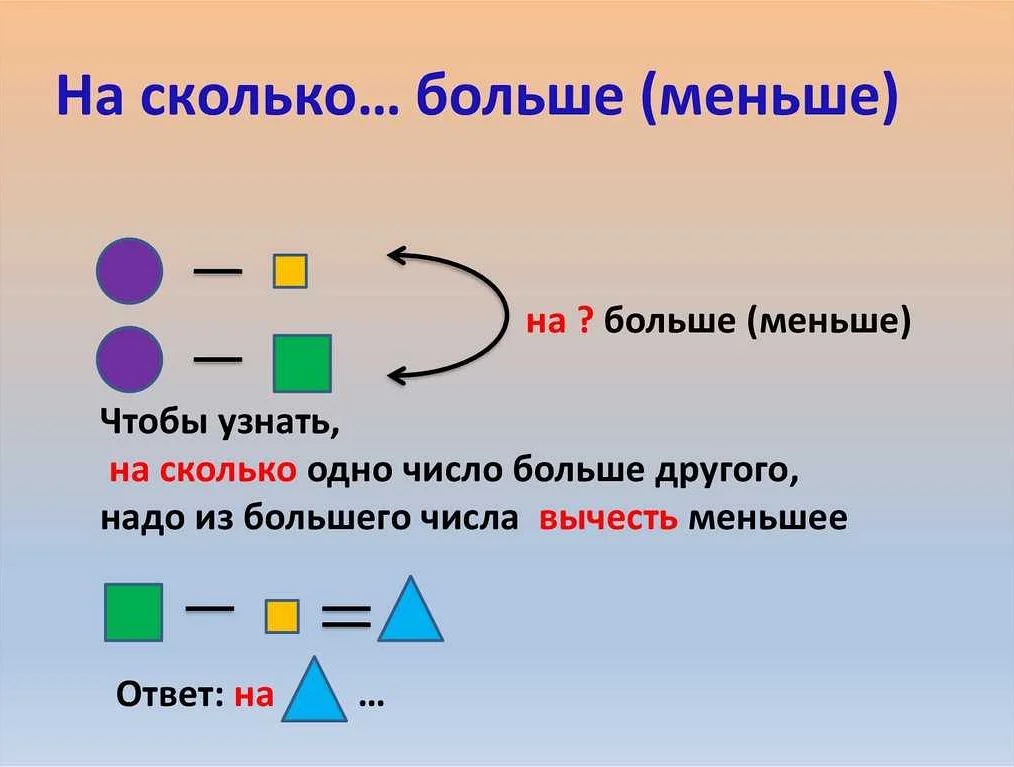
Относительная величина в математике используется для сравнения двух или более величин и определения, во сколько раз одна величина больше или меньше другой.

Для определения относительной величины нужно выполнить следующие шаги:

1. Найти разность между двумя величинами. Если первая величина больше, то разность будет положительной. Если первая величина меньше, то разность будет отрицательной.
2. Взять абсолютное значение разности, чтобы получить положительное число.
3. Разделить абсолютное значение разности на значение, с которым сравнивается исходная величина.
4. Полученное число показывает, во сколько раз первая величина больше или меньше второй.

Например, если первая величина равна 10, а вторая величина равна 5, то разность будет равна 10 — 5 = 5. Затем берем абсолютное значение разности, то есть |5| = 5. Для определения относительной величины делим абсолютное значение разности на вторую величину, то есть 5 / 5 = 1. Получается, что первая величина в данном случае в 1 раз больше второй.

Зная правила определения относительной величины, можно легко сравнивать и анализировать различные величины и их отношения друг к другу. Это полезный инструмент, который помогает понять, насколько одна величина превышает или уступает другой.

Определение относительной величины в математике

В математике относительная величина представляет собой показатель, который позволяет сравнивать две или более величины. С помощью относительной величины можно определить, во сколько раз одна величина больше или меньше другой.

Для определения относительной величины необходимо установить соотношение между двумя значениями. Для этого можно использовать различные математические операции, такие как деление, вычитание или умножение.

Если необходимо определить во сколько раз одно число больше другого, можно применить операцию деления. Для этого нужно разделить большую величину на меньшую. Результатом будет число, которое показывает, во сколько раз больше первое число по сравнению со вторым.

Например, если первое число равно 10, а второе — 5, то относительная величина будет равна 2. Это означает, что первое число в два раза больше второго.

В случае, если необходимо определить, во сколько раз одно число меньше другого, можно применить операцию деления. Нужно разделить меньшее число на большее. Результатом будет число, которое показывает, во сколько раз меньше первое число по сравнению со вторым.

Например, если первое число равно 5, а второе — 10, то относительная величина будет равна 0.5. Это означает, что первое число в два раза меньше второго.

Таким образом, определение относительной величины в математике позволяет осуществить сравнение двух величин и определить во сколько раз одна величина больше или меньше другой.

Понятие разности и отношения чисел

Разность двух чисел вычисляется путем вычитания одного числа из другого. Если число А больше числа В, то разность будет положительным числом. Если число А меньше числа В, то разность будет отрицательным числом.

Отношение двух чисел показывает, во сколько раз одно число больше или меньше другого числа. Отношение вычисляется путем деления одного числа на другое. Если полученное отношение больше 1, то первое число больше второго числа. Если полученное отношение меньше 1, то первое число меньше второго числа.

Например, если число А равно 10, а число В равно 5, то разность будет равна 5, так как 10 — 5 = 5. Отношение будет равно 2, так как 10 / 5 = 2.

Правила разности и отношения чисел могут быть полезными при решении различных задач, например, при сравнении размеров объектов, количества продуктов или времени.

ПримерыРазностьОтношение

А = 8, В = 3	5	2.667
А = 15, В = 20	-5	0.75
А = 12, В = 12	0	1

Использование понятий разности и отношения чисел помогает более точно определить и сравнить их значения, что является важным навыком в математике и реальной жизни.

Способы определения во сколько раз одно число больше или меньше другого

В математике существуют различные способы определения, во сколько раз одно число больше или меньше другого. Это важные концепции, которые помогают нам сравнивать и анализировать числа.

Первый способ — это разность между двумя числами. Если у нас есть два числа, то можно вычесть одно из другого и определить разность между ними. Если разность положительная, то первое число больше второго, если отрицательная — то первое число меньше второго.

Второй способ — это отношение двух чисел. Мы можем определить отношение одного числа к другому, разделив первое число на второе. Если результат больше 1, то первое число больше второго в указанное число раз. Если результат меньше 1, то первое число меньше второго в указанное число раз.

Третий способ — это процентное отношение. Мы можем определить процентное отношение одного числа к другому, вычислив разность между ними и делением этой разности на второе число. Затем умножим результат на 100, чтобы получить процентное отношение. Если результат больше 100%, то первое число больше второго в указанное число процентов. Если результат меньше 100%, то первое число меньше второго в указанное число процентов.

Важно понимать, что каждый из этих способов имеет свои особенности и применяется в разных ситуациях. Например, разность между числами более универсальна и может использоваться для сравнения любых чисел. В то же время, отношение и процентное отношение могут быть полезны при анализе данных и статистике.

Итак, знание способов определения во сколько раз одно число больше или меньше другого поможет нам сравнивать и анализировать числа, что является важным навыком в математике и других областях науки и жизни в целом.

Понятие пропорции и пропорциональности чисел

Чтобы определить, насколько одна величина больше или меньше другой, нужно сравнить их отношения. Пропорциональные числа имеют одинаковые отношения между собой, поэтому их можно сравнивать посредством умножения или деления.

Если две пары чисел обладают одинаковым отношением, то можно сказать, что они пропорциональны. Например, числа 4 и 8 пропорциональны числам 2 и 4, так как их отношение равно 2.

Чтобы определить, во сколько раз одно число больше или меньше другого, можно использовать пропорцию. Например, если отношение чисел 4 и 2 равно 2, то число 4 в два раза больше числа 2.

Пропорциональность чисел широко применяется в разных областях, таких как физика, экономика и геометрия. Понимание понятия пропорции и пропорциональности чисел поможет в решении различных задач и расчетах.

Использование процентов для определения относительной величины

Проценты могут быть одним из наиболее удобных способов определения относительной величины. Они позволяют выразить количественное соотношение между двумя числами или величинами.

Для определения, во сколько раз одно число больше или меньше другого, можно использовать проценты. Для этого необходимо выполнить следующие шаги:

1. Найдите разницу между двумя числами.

Если первое число больше второго, вычитаем меньшее число из большего. Если первое число меньше второго, вычитаем большее число из меньшего.

2. Определите, насколько процентов одно число отличается от другого.

Чтобы выразить эту разницу в процентах, можно воспользоваться формулой:

Разница в процентах = (Разница / Меньшее число) * 100%

3. Определите относительную величину в процентах.

Если первое число больше второго, полученное значение будет показывать, на сколько процентов первое число больше второго. Если первое число меньше второго, полученное значение будет показывать, на сколько процентов первое число меньше второго.

Например, если первое число равно 80, а второе число равно 60, разница между ними составляет 20. Для определения относительной величины в процентах, необходимо выполнить следующие вычисления:

Разница в процентах = (20 / 60) * 100% = 33,33%

Таким образом, первое число (80) больше второго числа (60) на 33,33%.

Определение относительного увеличения или уменьшения числа

Относительное увеличение или уменьшение числа позволяет определить, насколько процентов значение числа изменилось в сравнении с его исходным значением. Этот показатель позволяет сравнивать разные значения и определять, во сколько раз одно число больше или меньше другого.

Для определения относительного увеличения или уменьшения числа необходимо выполнить следующий набор действий:

1. Найти разность между новым значением числа и его исходным значением.
2. Разделить полученную разность на исходное значение числа.
3. Умножить полученное значение на 100, чтобы получить процентное отношение.

Если результат вычислений положительный, то это означает относительное увеличение числа. Если результат отрицательный, то это означает относительное уменьшение числа.

Например, пусть у нас есть число 100 и оно увеличилось до 150. Для определения относительного увеличения необходимо выполнить следующие действия:

Разность между новым значением числа и его исходным значением: 150 — 100 = 50.

Разделение полученной разности на исходное значение числа: 50 / 100 = 0.5.

Умножение полученного значения на 100: 0.5 * 100 = 50%.

Таким образом, число увеличилось на 50%.

Аналогичным образом можно определить относительное уменьшение числа. Например, если число уменьшилось с 200 до 150:

Разность между новым значением числа и его исходным значением: 150 — 200 = -50.

Разделение полученной разности на исходное значение числа: -50 / 200 = -0.25.

Умножение полученного значения на 100: -0.25 * 100 = -25%.

Таким образом, число уменьшилось на 25%.

Относительное увеличение или уменьшение числа является важным инструментом для анализа данных и сравнения различных значений. Правильное определение этого показателя помогает более точно оценить изменения и сделать соответствующие выводы.

Примеры и задачи по определению во сколько раз больше или меньше

Определение во сколько раз одно число больше или меньше другого очень полезно в математике. Давайте рассмотрим несколько примеров и задач, чтобы лучше понять этот концепт.

Пример 1:

Пусть у нас есть два числа: 10 и 5. Чтобы определить, во сколько раз одно число больше или меньше другого, мы делим большее число на меньшее число.

В данном случае, 10 больше 5, поэтому мы делим 10 на 5:

10 / 5 = 2

То есть, число 10 в два раза больше числа 5.

Пример 2:

Теперь рассмотрим числа 15 и 3. Делим большее число на меньшее число:

15 / 3 = 5

Таким образом, число 15 в пять раз больше числа 3.

Задача:

У нас есть два числа: 12 и 8. Определите, во сколько раз одно число больше или меньше другого:

1. Делим большее число на меньшее число:
2. 12 / 8 = 1.5

Число 12 в 1.5 раза больше числа 8.

Задача:

Теперь попробуйте решить задачу самостоятельно. У нас есть два числа: 24 и 6. Определите, во сколько раз одно число больше или меньше другого.

1. Делим большее число на меньшее число:
2. 24 / 6 = 4

Число 24 в 4 раза больше числа 6.

Теперь вы знакомы с правилами определения во сколько раз одно число больше или меньше другого. Попрактикуйтесь в решении разных задач, чтобы закрепить этот математический навык.

Вопрос-ответ:

Как определить, во сколько раз одно число больше другого?

Для определения во сколько раз одно число больше другого, нужно разделить большее число на меньшее. Результат этого деления будет показывать, во сколько раз одно число больше другого.

Как определить, во сколько раз одно число меньше другого?

Для определения во сколько раз одно число меньше другого, нужно разделить меньшее число на большее. Результат этого деления будет показывать, во сколько раз одно число меньше другого.

Как использовать правило «во сколько раз больше или меньше» в реальной жизни?

Правило «во сколько раз больше или меньше» может быть полезным во многих ситуациях. Например, оно может помочь сравнить размеры объектов, стоимость продуктов, количество времени, затраченное на выполнение задачи, и многое другое.

Можно ли использовать правило «во сколько раз больше или меньше» для сравнения дробей?

Да, можно. Правило «во сколько раз больше или меньше» можно применять для сравнения дробей. Нужно просто выполнить деление одной дроби на другую и результат покажет, во сколько раз одна дробь больше или меньше другой.

Видео по теме: