Что такое р а в математике

Равенство (r) в математике — это отношение между двумя математическими объектами, которые считаются равными. В данной статье мы рассмотрим понятие равенства и его основные свойства в математике.

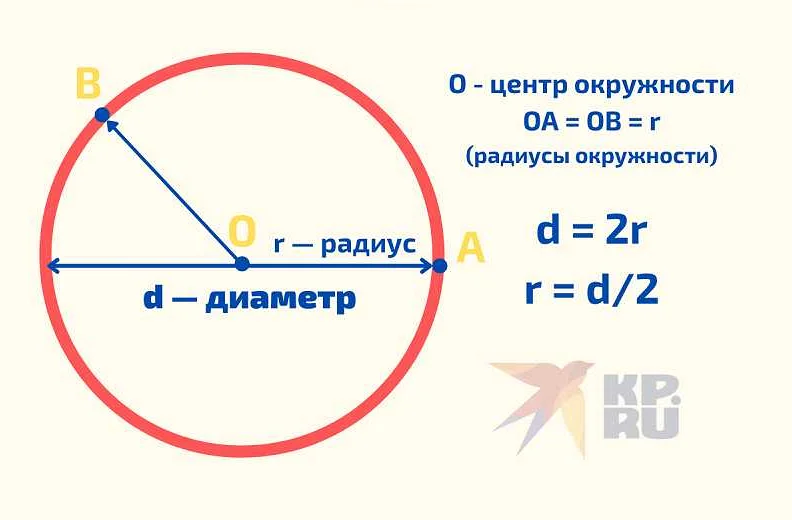
Р — это одна из наиболее фундаментальных и широко используемых констант в математике. Это иррациональное число, которое представляет собой отношение длины окружности к ее диаметру. Обозначается символом «р» и имеет приближенное значение 3,14159. Однако, десятичная запись не исчерпывает всю бесконечность знаков числа «р».

Константа «р» обладает рядом уникальных свойств и используется во многих областях математики, физики, инженерии и других науках. Одно из самых известных свойств «р» — его бесконечность. Несмотря на то, что десятичная запись числа «р» ограничена, оно может быть выражено в виде бесконечной десятичной дроби или с помощью различных математических формул и рядов. Бесконечность «р» делает его непредсказуемым и уникальным числом.

Пример использования числа «р» — вычисление площади окружности. Для данной фигуры площадь равна произведению квадрата радиуса на «р». Эта формула широко применяется в геометрии и позволяет точно определить площадь окружности, даже если ее радиус не является целым числом или имеет дробное значение.

Таким образом, число «р» играет важную роль в математике и науках, предоставляя уникальные возможности для вычислений и моделирования. Его бесконечность и непредсказуемость делают его фундаментальным элементом многих математических концепций и теорий.

Определение числа р в математике

Число р является основным объектом изучения теории чисел. Оно имеет много свойств и особенностей, которые делают его важным элементом в математике.

Например, р — бесконечное множество, так как простых чисел бесконечное количество. Также, для любого числа n, всегда можно найти простое число p такое, что p > n.

Свойства числа р:

1. Р — бесконечное множество

2. Для любого числа n, всегда можно найти простое число p такое, что p > n

3. Число простых чисел меньше n примерно равно n / ln(n), где ln(n) — натуральный логарифм n

Число р играет важную роль в различных областях математики и имеет множество приложений в науке и технологии.

Основные свойства числа р

π = длина окружности / диаметр

Однако число π не является рациональным числом и не может быть представлено в виде десятичной дроби или конечной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной десятичной деся

Примеры применения числа р в математике

Число р играет важную роль в различных областях математики. Ниже приведены некоторые примеры его применения:

1. Вероятность и статистика:

Число р используется для вычисления вероятностей в статистике и теории вероятностей. Например, в задаче о бросании игральной кости с шестью гранями вероятность выпадения конкретного числа на кости равна 1/6, так как у кости есть шесть равновероятных исходов.

2. Геометрия:

Число р используется в геометрии для вычисления длин окружности и площадей кругов. Длина окружности равна произведению числа р на двойной радиус (2рr), а площадь круга равна квадрату числа р, умноженному на радиус (р^2r).

3. Анализ:

Число р играет важную роль в анализе, особенно в дифференциальном и интегральном исчислении. Оно используется для представления бесконечно малой величины, такой как дифференциал или интеграл. Например, дифференциал функции f(x) обозначается как df(x), а интеграл функции f(x) обозначается как ∫f(x) dx.

4. Криптография:

Число р также используется в криптографии, науке о защите информации. Оно используется в алгоритмах шифрования, генерации случайных чисел и проверке целостности данных. Например, в алгоритме RSA, число р используется для генерации ключей и шифрования данных.

Это лишь некоторые примеры применения числа р в математике. Оно является одним из фундаментальных чисел и находит широкое применение в различных областях науки и техники.

Значение числа р в математических формулах и уравнениях

Число р появляется во многих формулах и уравнениях, связанных с геометрией, тригонометрией, анализом и другими областями математики. Оно является соотношением длины окружности к ее диаметру и обозначается греческой буквой π.

Рассмотрим некоторые примеры использования числа р в математических формулах:

— Формула для вычисления площади круга: площадь круга равна произведению квадрата радиуса на число пи (S = πr²).

— Формула для вычисления длины окружности: длина окружности равна произведению диаметра на число пи (C = πd).

— Формула для вычисления периметра окружности: периметр окружности равен произведению диаметра на число пи (P = πd).

— Формула для вычисления площади сектора: площадь сектора равна произведению доли окружности (в радианах) на квадрат радиуса, умноженное на число пи (S = πr²θ/360°).

— Формула для вычисления объема цилиндра: объем цилиндра равен произведению площади основания на высоту (V = πr²h).

Это только некоторые примеры использования числа р в математических формулах. Оно имеет множество других применений и связей с другими математическими константами и функциями.

Знание значения числа р позволяет математикам и инженерам точно рассчитывать и предсказывать поведение объектов и процессов, связанных с окружностями и круговыми формами.

Влияние числа р на математические расчеты

Одним из примеров влияния числа р на математические расчеты является его использование в формулах для вычисления площади и объема геометрических фигур. Например, для вычисления площади круга используется формула S = πr², где р — радиус круга, а π — число пи, приближенное к 3,14. Число р является ключевым элементом в этой формуле и определяет площадь круга.

Также число р имеет важное значение при решении уравнений и систем уравнений. Оно используется для определения корней уравнений и для анализа их свойств. Величина р может влиять на число и характер корней уравнений.

Величина р также играет важную роль в вероятностных расчетах. Она используется для определения вероятности событий и для расчета вероятностей различных комбинаций и вариантов. Например, в формуле для расчета вероятности события A используется величина р: P(A) = р/N, где р — число благоприятных исходов, N — общее число возможных исходов.

Кроме того, число р является основой для ряда других математических концепций и теорий. Например, р используется в теории вероятностей, теории чисел, математической статистике и других областях математики.

Таким образом, число р оказывает значительное влияние на математические расчеты и является неотъемлемой частью многих математических формул и концепций.

Способы вычисления числа р

Существует несколько способов вычисления числа р:

1. Геометрический метод: Рассмотрите круг и его диаметр. Проведите окружность вокруг круга и измерьте окружность и диаметр. Отношение окружности к диаметру будет приближенно равно числу р.
2. Арктангенсальный метод: Используйте арктангенсальные функции, такие как тангенс и арктангенс. С помощью формулы atan(1) = π/4 можно вычислить число р.
3. Ряды: Число р может быть приближенно вычислено с помощью бесконечного ряда, такого как ряд Лейбница или ряд Нилаканта.

Это лишь несколько способов, которые можно использовать для вычисления числа р. Однако точное значение числа р является неразрешимой задачей, и его значение было вычислено с максимальной точностью на сегодняшний день. Число р играет важную роль в различных областях науки и инженерии, и его изучение имеет большое значение в математике.

Применение числа р в других науках и областях знаний

Физика: В физике число р встречается во многих формулах и уравнениях. Например, оно используется в законе всемирного тяготения Ньютона для определения силы притяжения между двумя объектами. Также число р влияет на распределение электрического заряда вокруг точечного объекта.

Инженерия: В инженерии число р применяется при проектировании круглых объектов и конструкций, таких как колеса, шестерни и трубы. Оно позволяет определить длину окружности и площадь круга, а также решать задачи связанные с расчетом радиуса и диаметра.

Компьютерная графика: В компьютерной графике число р используется для определения формы и визуализации геометрических объектов, таких как круги, эллипсы и окружности. Оно позволяет создавать реалистичные изображения и анимацию.

Статистика: В статистике число р применяется для оценки и предсказания вероятности различных событий. Оно используется для построения графиков, расчета вероятностей и выполнения статистических тестов.

Финансы: В финансовой математике число р используется для расчета сложных процентов и дисконтирования денежных потоков. Оно позволяет определить стоимость инвестиций и рассчитать будущую стоимость денег.

Применение числа р в различных науках и областях знаний подчеркивает его универсальность и важность в понимании мира и решении различных задач.

Вопрос-ответ:

Что такое р в математике?

В математике р — это символ, который обозначает множество всех действительных чисел.

Какие свойства имеет р в математике?

Множество р обладает следующими свойствами: неограниченность, плотность и полнота.

Что означает неограниченность р в математике?

Неограниченность р означает, что множество р содержит все действительные числа, включая как положительные, так и отрицательные бесконечности.

Что значит плотность р в математике?

Плотность р означает, что между любыми двумя числами р всегда можно найти третье число.

Можно ли привести примеры чисел, принадлежащих множеству р?

Да, конечно! Например, 0, 1, -1, 3.14, -2.71828 и т.д. — все эти числа принадлежат множеству р.

Какое определение имеет символ «р» в математике?

В математике символ «р» часто используется для обозначения различных величин, таких как радиус, вероятность, плотность и других.

Видео по теме: