Константа что это в математике

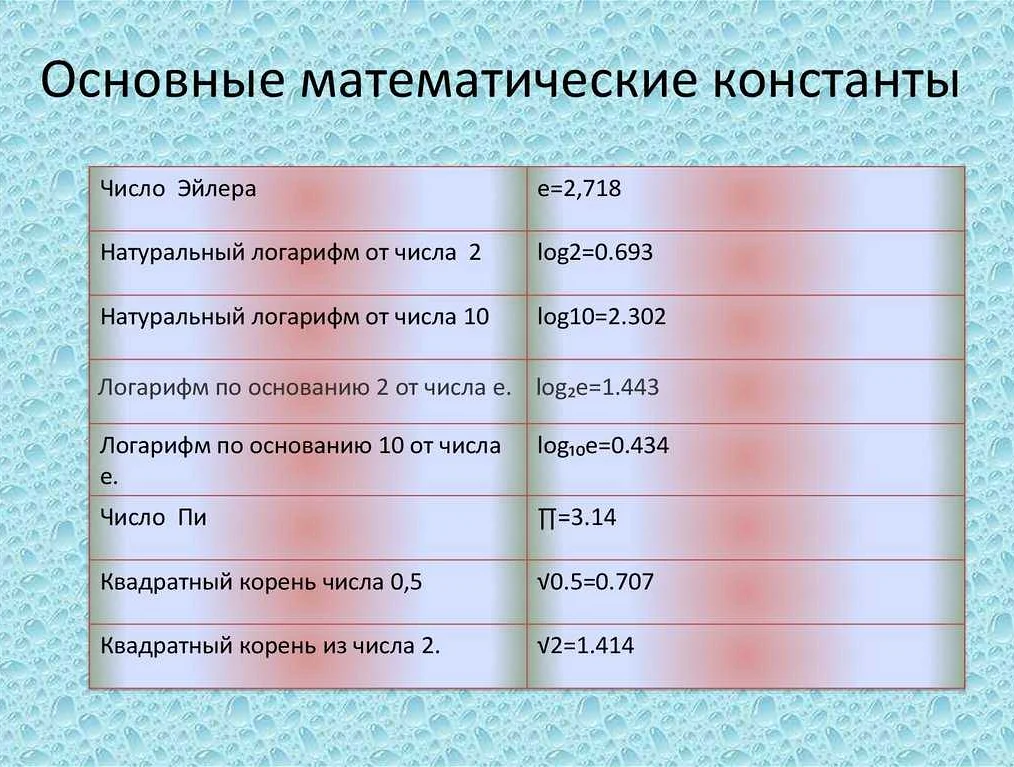
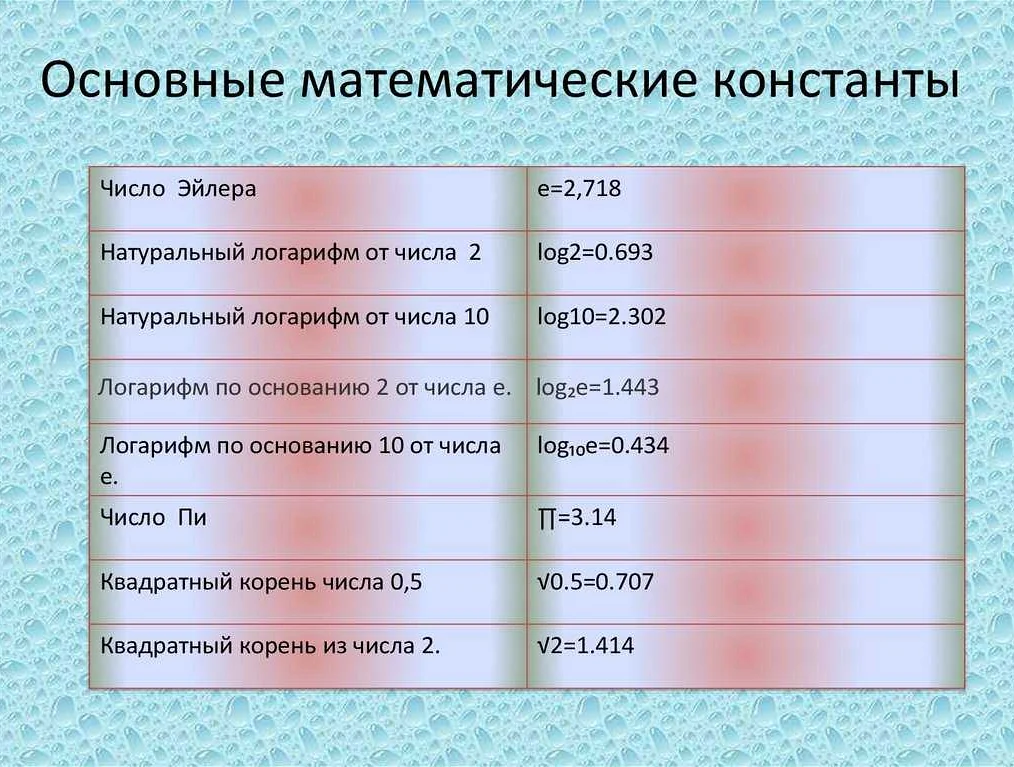
Константа в математике – это числовое значение, которое не меняется в течение всего вычисления или в рамках определенного контекста. Это может быть число, символ или выражение, которое используется для определения и описания различных математических объектов и законов. Константы играют важную роль в математических моделях и уравнениях, обеспечивая постоянство и стабильность в вычислениях и анализе данных. Понимание и использование констант является основополагающим для работы в математике и других науках, где математические методы применяются.

В математике константа — это значение, которое остается постоянным в течение всего вычисления или анализа. Она не изменяется и используется для отображения фиксированной величины или параметра в уравнениях, формулах или алгоритмах. Константы являются основными строительными блоками математических выражений и играют важную роль в различных областях математики, физики и других наук.

Одной из наиболее известных констант является число π (пи) — отношение длины окружности к ее диаметру. Значение π приближенно равно 3,14159 и используется в геометрии, тригонометрии, анализе и других математических дисциплинах. Еще одной важной константой является e — основание натурального логарифма, которое приближенно равно 2,71828. Число e широко применяется в экономике, финансах, статистике и других областях, связанных с ростом и изменением величин.

Константы также могут быть определены как физические постоянные, которые имеют фиксированное значение в природе. Например, скорость света в вакууме (299 792 458 метров в секунду), гравитационная постоянная (6,67430 x 10^-11 метров в кубе на килограмм в секунду в квадрате) и постоянная Планка (6,62607015 x 10^-34 джоуля в секунду).

Константы играют ключевую роль в математике, облегчая вычисления, анализ и моделирование различных явлений и процессов. Они позволяют установить фиксированные связи между различными переменными и сделать выводы о поведении системы или объекта в целом. Благодаря константам математики и другие ученые могут раскрыть законы природы, строить точные модели и предсказывать результаты экспериментов и наблюдений.

В данной статье мы рассмотрели определение константы в математике и привели несколько примеров ее использования. Константы являются важными инструментами для работы с числами и формулами, и их знание позволяет более глубоко понять основы математики и научиться применять ее в решении различных задач и задач наук.

Что такое константа в математике?

Константы обычно обозначаются буквами латинского алфавита, например, a, b, c. Они могут представлять собой числа, буквы или символы, которые имеют фиксированное значение и не изменяются в процессе решения математической задачи.

Примерами констант могут быть:

КонстантаЗначение

π (пи)	3.14159…
e (экспонента)	2.71828…
гравитационная постоянная	6.67430 × 10^-11 м^3 кг^-1 с^-2

Константы широко используются в математике для упрощения вычислений и формулирования законов и теорем. Они позволяют задавать фиксированные значения, которые остаются неизменными во всех рассматриваемых случаях.

Видео по теме:

Определение и основные свойства

Основные свойства констант в математике:

• Константа представляет собой фиксированное значение и не меняется в ходе вычислений или преобразований;
• Константы могут быть использованы для описания и обозначения определенных объектов или явлений, таких как математические константы (например, число Пи, экспонента, геометрические константы и т.д.);
• Константы могут использоваться в уравнениях и функциях для задания определенных условий или ограничений;
• Константы могут быть использованы для создания математических моделей и прогнозирования результатов;
• Константы обычно обозначаются заглавными латинскими буквами.

В математике константы играют важную роль, поскольку они позволяют нам описывать и анализировать различные явления и объекты, а также проводить различные вычисления и преобразования. Они являются одной из основных составляющих математического формализма и позволяют нам строить точные и надежные модели реального мира.

Примеры использования

Константы широко используются в математике для обозначения известных и неизменных величин. Некоторые из наиболее распространенных примеров использования констант:

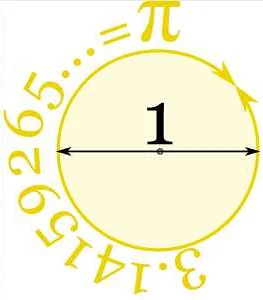
1. Пи (π) — это одна из наиболее известных математических констант. Она представляет отношение длины окружности к ее диаметру и приближенно равняется 3,14159. Пи используется во многих разделах математики, физики и инженерии, включая геометрию, тригонометрию и анализ.

2. Например, скорость света в вакууме (c) — это фундаментальная физическая константа, определяющая максимальную скорость распространения информации во Вселенной. Скорость света приближенно равна 299 792 458 метров в секунду и является неизменной величиной во всех инерциальных системах отсчета.

3. Еще одним примером использования констант является число Авогадро (NA), которое определяет количество молекул в одном молье вещества. Значение константы Авогадро примерно равно 6,02214076 × 10^23 молекул в одном молье.

4. Константа гравитационной постоянной (G) используется в законе всемирного тяготения, который описывает взаимодействие гравитационных сил между телами. Значение константы гравитационной постоянной приближенно равно 6,67430 × 10^(-11) кг^(-1)·м^3·с^(-2).

5. Еще одним примером константы является число Эйлера (e), которое представляет собой основание натурального логарифма. Значение числа Эйлера приближенно равно 2,71828 и оно широко используется в математическом анализе и других разделах математики.

Это лишь некоторые примеры использования констант в математике и других науках. Константы играют важную роль в точности и универсальности математических моделей и уравнений, позволяя нам более полно описывать и понимать мир вокруг нас.

Вопрос-ответ:

Что такое константа в математике?

В математике константа — это значение, которое не изменяется в течение всего вычисления или задачи. Она не зависит от переменных или других факторов и остается постоянной.

Какие примеры констант в математике?

Примерами констант в математике могут служить числа, которые неизменны: такие, как число π (пи), число e (основание натурального логарифма), а также математические константы, такие как синус 30 градусов.

Зачем нужны константы в математике?

Константы в математике являются важными инструментами, используемыми для определения и изучения различных математических явлений и закономерностей. Они помогают сделать математические модели более точными и позволяют проводить более сложные вычисления.

Каким образом применяются константы в математике?

Константы используются в математике для определения формул, уравнений и законов. Они также могут использоваться для вычислений, приближений и аппроксимаций. Например, константа π используется в формулах для вычисления длины окружности и площади круга.

Как можно определить константу в математике?

Константа в математике может быть определена как значение, которое остается постоянным в течение всего вычисления или задачи. Она может быть явно задана в формуле или уравнении, или быть результатом определенных математических операций или измерений.

Что такое константа в математике?

Константа в математике — это числовое значение, которое остается неизменным в течение всего вычислительного процесса или в заданном контексте. Она представляет собой фиксированное значение, которое не зависит от других переменных или параметров.

Константы в различных областях математики

Константы играют важную роль в различных областях математики. Они представляют собой фиксированные значения, которые не изменяются в течение рассматриваемого контекста или задачи.

В геометрии одной из наиболее известных констант является «пи» (π). Она представляет отношение длины окружности к ее диаметру и имеет приближенное значение 3,14159. Константа «пи» широко используется в геометрических и тригонометрических расчетах и формулах.

В алгебре одной из наиболее известных констант является «е» (e). Она представляет собой основание натурального логарифма и имеет приближенное значение 2,71828. Константа «е» широко используется в экспоненциальных и логарифмических функциях и формулах.

В физике и инженерии также используются множество констант. Например, скорость света в вакууме (c) составляет приблизительно 299 792 458 метров в секунду. Константы, такие как ускорение свободного падения (g) или постоянная Планка (h), играют важную роль в физических законах и уравнениях.

В статистике одной из наиболее известных констант является «корень из двух» (√2). Она представляет собой иррациональное число и используется, например, в формулах для вычисления стандартного отклонения.

Область математикиПримеры констант

Геометрия	Пи (π)
Алгебра	Е (e)
Физика и инженерия	Скорость света (c), ускорение свободного падения (g), постоянная Планка (h)
Статистика	Корень из двух (√2)

Константы являются неотъемлемой частью математики и играют важную роль в различных областях. Они помогают описывать и решать различные задачи, а также имеют широкое применение в научных и инженерных расчетах.

Использование констант в уравнениях и формулах

Константы играют важную роль в математике и широко используются в уравнениях и формулах. Они представляют собой значения, которые не изменяются в процессе вычислений и остаются постоянными.

Константы могут быть использованы для задания определенных параметров или свойств объектов или явлений. Они могут также представлять собой физические постоянные, такие как скорость света, гравитационная постоянная или число Пи.

Константы могут быть включены в уравнения и формулы для облегчения вычислений и повышения точности результатов. Они могут быть использованы для определения связи между различными переменными в рамках математической модели или для задания значений, которые остаются неизменными при различных условиях.

Например, в уравнении окружности используется константа Пи (π), которая представляет отношение длины окружности к ее диаметру. Также в уравнении закона всемирного тяготения Ф = G * (m1 * m2) / r^2 использована гравитационная постоянная G, которая представляет силу притяжения между двумя телами.

Использование констант позволяет упростить и стандартизировать математические вычисления, а также обеспечивает единообразие и точность результатов.

Константы в алгебре и геометрии

Константы также широко используются в алгебре и геометрии. В алгебре константы могут представлять числа, которые не меняются в рамках рассматриваемой задачи или уравнения. Они обычно обозначаются заглавными буквами и используются для задания значений переменных или коэффициентов.

В геометрии константы могут представлять свойства геометрических фигур, которые не меняются при их преобразованиях или взаимодействии с другими фигурами. Например, длина окружности или площадь прямоугольника являются константами, так как они не зависят от положения или формы фигуры.

Константы в алгебре и геометрии играют важную роль при решении уравнений, построении графиков и изучении свойств фигур. Они позволяют установить базовые значения и свойства объектов, что упрощает математические вычисления и анализ задач.

Примеры констант в алгебреПримеры констант в геометрии

π (пи)	Длина окружности
e (число Эйлера)	Площадь прямоугольника
гравитационная постоянная	Углы в треугольнике
скорость света	Радиусы и диаметры окружности

Использование констант в алгебре и геометрии позволяет более точно и удобно работать с числами и фигурами, упрощает вычисления и позволяет получать более точные результаты.

Роль констант в математических моделях

Одна из основных функций констант в математических моделях — задание начальных условий или параметров модели. Константы могут определять физические свойства объектов, геометрические параметры или другие характеристики системы, в которой происходит моделирование.

Например, в математической модели движения тела под действием силы тяжести, константой может быть масса тела, гравитационная постоянная и высота начального положения. Задав эти константы, можно вычислить траекторию движения тела в пространстве и определить его конечное положение.

Константы также используются для установления связей между различными переменными в математической модели. Например, в формуле для вычисления площади круга, константа π (пи) является неизменным значением, которое связывает радиус круга и его площадь.

Использование констант в математических моделях позволяет точнее описать реальные явления и процессы, а также упрощает вычисления и анализ результатов. Константы — это надежные и постоянные значения, которые помогают установить основные параметры модели и обеспечить ее правильное функционирование.

Значение констант в физике и естествознании

Одной из наиболее известных констант в физике является скорость света в вакууме, обозначаемая символом c. Ее значение составляет примерно 299 792 458 метров в секунду. Скорость света является максимальной скоростью передачи информации и имеет фундаментальное значение в теории относительности.

Еще одной важной константой является постоянная Планка, обозначаемая символом h. Ее значение составляет примерно 6,62607015 × 10^-34 Дж·с. Постоянная Планка связана с квантовой механикой и используется для определения энергии элементарных частиц.

Также можно выделить гравитационную постоянную, обозначаемую символом G. Ее значение составляет примерно 6,67430 × 10^-11 Н·м^2/кг^2. Гравитационная постоянная определяет силу притяжения между объектами и играет важную роль в теории гравитации.

Константы в физике и естествознании помогают установить фундаментальные законы природы и проводить точные измерения. Они являются неизменными величинами, которые служат основой для построения научных моделей и теорий.