Что такое радиус окружности 4 класс математика

Радиус окружности в математике — это отрезок, соединяющий центр окружности с любой ее точкой. В 4 классе на уроках математики изучаются основные понятия геометрии, включая радиус окружности. Ученики учатся измерять и находить радиус окружности, а также применять его в решении задач и построении геометрических фигур. Познакомиться с понятием радиуса окружности можно на простых и доступных примерах, которые помогут ученикам лучше освоить материал и понять его практическое применение.

Радиус окружности — одно из важнейших понятий в математике, которое изучается уже среди четвероклассников. Это основа для понимания геометрических фигур и их свойств. Окружность — это геометрическая фигура, состоящая из всех точек, находящихся на одинаковом расстоянии от центра. Именно этот расстояние и называется радиусом окружности.

Радиус обозначается буквой «r» и является отрезком, соединяющим центр окружности с любой точкой на ней. Интересно, что длина радиуса окружности одинакова для всех ее точек. Он определяет размер окружности и является половиной диаметра. Радиус окружности имеет и другие важные свойства, которые помогают нам решать разнообразные задачи в математике.

Например, зная радиус окружности, мы можем вычислить ее длину или площадь. Длина окружности равна удвоенному произведению радиуса на число «пи» (π), которое приближенно равно 3,14. А площадь окружности вычисляется по формуле: π*r^2, где r — радиус окружности. Понимание и умение работать с радиусом окружности позволяет нам легко решать задачи как на практике, так и в повседневной жизни.

Определение радиуса окружности

Радиус является одним из основных понятий в геометрии окружностей. Он определяет размер окружности и используется во многих математических формулах и задачах.

Радиус можно измерить с помощью линейки или другого инструмента для измерения длины. Для получения точного значения радиуса необходимо измерять от центра окружности до точки на ее границе.

Радиус является половиной диаметра окружности. Диаметр — это отрезок, соединяющий две точки на границе окружности и проходящий через ее центр. Диаметр обозначается буквой «d».

Радиус окружности может быть разной длины в разных окружностях. Он всегда положительный и не может быть отрицательным.

Зная радиус окружности, можно вычислить ее площадь и длину. Формулы для вычисления площади и длины окружности связаны с радиусом и используют его значение.

Свойства радиуса окружности

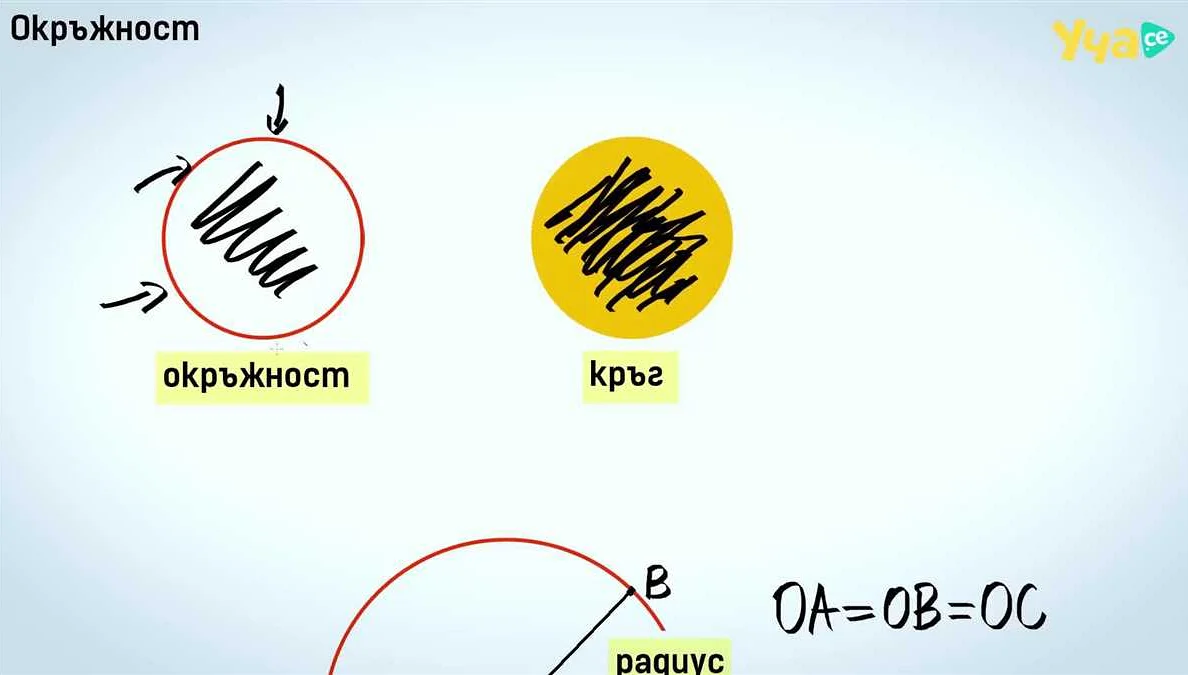
1. Длина радиуса одинакова для всех точек на окружности. Это означает, что если мы измерим расстояние от центра окружности до любой точки на ее границе, то получим одинаковое значение.
2. Радиус является половиной диаметра окружности. Диаметр — это отрезок, проходящий через центр окружности и соединяющий две противоположные точки на ее границе. Таким образом, диаметр равен удвоенной длине радиуса.
3. Радиус перпендикулярен к касательной, проведенной в точке соприкосновения с окружностью. Это значит, что радиус и касательная, проведенные к окружности, образуют прямой угол.
4. Радиус является одним из элементов, необходимых для вычисления площади и длины окружности. Площадь окружности можно найти по формуле S = πr², где π (пи) — это математическая константа, приближенное значение которой равно 3,14. Длину окружности можно найти по формуле L = 2πr.

Таким образом, радиус окружности играет важную роль в геометрии и позволяет определить множество характеристик и свойств этой фигуры.

Измерение радиуса окружности

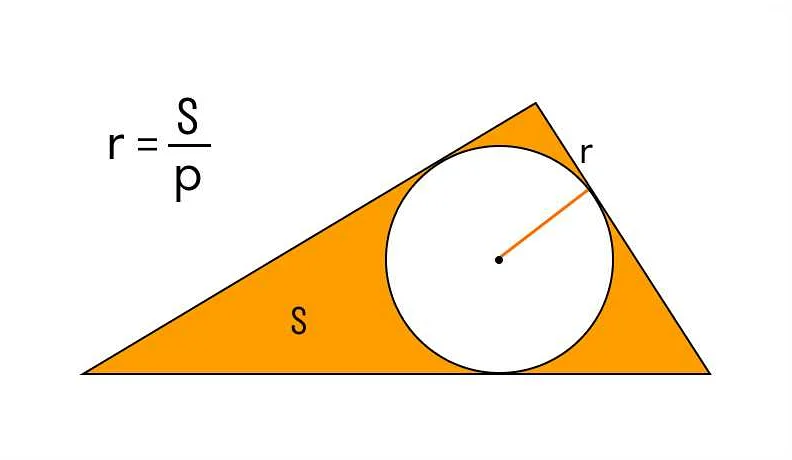
Измерение радиуса окружности может быть представлено различными единицами измерения, такими как сантиметры, метры и т. д. Для измерения радиуса можно использовать линейку или мерную ленту.

При измерении радиуса окружности необходимо помнить о некоторых правилах. Сначала нужно определить центр окружности — точку, которая является серединой окружности. Затем с помощью линейки или мерной ленты нужно измерить расстояние от центра до любой точки на окружности. Полученное значение будет радиусом окружности.

Радиус окружности является важным параметром при решении различных задач и формул, связанных с этой геометрической фигурой. Например, радиус используется для вычисления площади окружности, длины окружности и других характеристик.

Таким образом, измерение радиуса окружности является неотъемлемой частью изучения геометрии и позволяет более точно определить характеристики этой фигуры.

Формула для вычисления радиуса окружности

Формула для вычисления радиуса окружности выглядит следующим образом:

Радиус (r) = Длина окружности (l) / (2 * Пи (π))

В этой формуле:

• Радиус (r) — искомое значение радиуса;
• Длина окружности (l) — известное значение длины окружности;
• Пи (π) — математическая константа, которая примерно равна 3,14.

Чтобы вычислить радиус окружности, необходимо знать длину окружности. Длина окружности может быть вычислена, если известен ее диаметр или периметр.

Например, если известна длина окружности (l), равная 10 см, мы можем использовать формулу для вычисления радиуса:

Радиус (r) = 10 см / (2 * 3,14) ≈ 1,59 см

Таким образом, радиус окружности равен примерно 1,59 см.

Связь радиуса окружности с другими характеристиками

Сначала стоит отметить, что радиус окружности является половиной диаметра. Диаметр окружности — это отрезок, проходящий через ее центр и образующий прямую линию. Таким образом, радиус окружности можно выразить через диаметр, умножив его на 0.5.

Следующая связь радиуса окружности — это его влияние на длину окружности. Длина окружности можно найти по формуле: Длина = 2πR, где R — радиус окружности, а π (пи) — математическая константа, примерное значение которой равно 3.14. Таким образом, чем больше радиус окружности, тем больше будет ее длина.

Также радиус окружности связан с площадью окружности. Площадь можно найти по формуле: Площадь = πR^2, где R — радиус окружности. Заметим, что площадь окружности пропорциональна квадрату радиуса.

И наконец, радиус окружности влияет на высоту и площадь сектора окружности. Сектор окружности — это фигура, ограниченная дугой окружности и двумя ее радиусами. Высота и площадь сектора зависят от радиуса: чем больше радиус, тем больше высота и площадь сектора.

Таким образом, радиус окружности имеет связь с диаметром, длиной окружности, площадью окружности и характеристиками сектора окружности. Понимание этих связей поможет вам лучше понять и использовать радиус окружности в математике.

Видео по теме:

Вопрос-ответ:

Что такое радиус окружности?

Радиус окружности — это отрезок, соединяющий центр окружности с любой ее точкой.

Как найти радиус окружности?

Чтобы найти радиус окружности, нужно разделить диаметр окружности на 2.

Зачем нужен радиус окружности?

Радиус окружности используется для решения различных задач и формул, связанных с окружностями. Например, он необходим для вычисления площади и длины окружности.

Какие еще свойства имеет радиус окружности?

Радиус окружности также является прямым отрезком, перпендикулярным к касательной в точке соприкосновения и имеющим равные длины в одной окружности.

Примеры задач с радиусом окружности

1. Найдите длину окружности, если ее радиус равен 5 см.

Решение: Длина окружности вычисляется по формуле L = 2πr, где r — радиус окружности, а π — математическая константа, примерно равная 3,14. Подставляя значения в формулу, получаем L = 2 * 3,14 * 5 = 31,4 см.

2. У Маши есть кусок проволоки длиной 30 см. Она хочет сделать из него круглую рамку для фотографии, такую, чтобы радиус равнялся 5 см. Она может сделать такую рамку?

Решение: Для решения этой задачи нужно определить, достаточно ли длины проволоки для создания окружности с радиусом 5 см. Длина окружности вычисляется по формуле L = 2πr. Подставим значения в формулу: L = 2 * 3,14 * 5 = 31,4 см. Так как длина проволоки равна 30 см, Маша не сможет сделать рамку с радиусом 5 см, так как проволока не хватит.

3. Радиус окружности равен 7 см. Найдите площадь круга.

Решение: Площадь круга вычисляется по формуле S = πr^2, где r — радиус окружности, а π — математическая константа, примерно равная 3,14. Подставляя значения в формулу, получаем S = 3,14 * 7^2 = 3,14 * 49 = 153,86 см^2.

4. Радиус круга увеличили в 2 раза. Во сколько раз увеличилась площадь круга?

Решение: Площадь круга вычисляется по формуле S = πr^2. Если радиус увеличился в 2 раза, значит новый радиус будет равен 2r. Подставляем новое значение радиуса в формулу и получаем S’ = π(2r)^2 = π4r^2 = 4πr^2. Ответ: площадь круга увеличилась в 4 раза.

5. Радиус окружности равен 3 см. Найдите диаметр окружности.

Решение: Диаметр окружности вычисляется по формуле D = 2r, где r — радиус окружности. Подставляем значение радиуса в формулу и получаем D = 2 * 3 = 6 см.

Применение радиуса окружности в реальной жизни

1. Строительство. В строительстве радиус окружности используется при проектировании и построении круглых форм и объектов. Например, при создании арок и куполов радиус окружности играет важную роль в определении размеров и формы конструкции.

2. Дорожное движение. В области дорожного движения радиус окружности применяется для создания изгибов дорог и поворотов. Радиус определяет геометрические параметры дорожной разметки и помогает обеспечить безопасность движения.

3. Медицина. В медицине радиус окружности используется при измерении размеров и формы органов человека. Например, при проведении УЗИ (ультразвукового исследования) радиус окружности помогает определить размеры фолликула яичника или опухоли.

4. Технические решения. Радиус окружности применяется в различных технических решениях, например, при создании колес и шестерен. Радиус определяет размеры и пропорции деталей, обеспечивая их правильную работу.

Таким образом, радиус окружности играет важную роль в различных сферах нашей жизни, помогая определить размеры, форму и геометрические параметры различных объектов и конструкций.