Что такое радиус в математике 5 класс

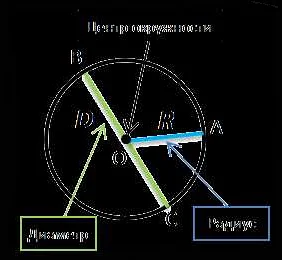
Радиус в математике для учеников 5 класса — это отрезок, соединяющий центр окружности с любой ее точкой. Узнайте, как определить и измерить радиус, а также узнайте основные свойства и задачи, связанные с радиусом окружности.

Радиус — одно из важнейших понятий геометрии, с которым знакомятся ученики уже в пятом классе. Он используется для определения различных характеристик геометрических фигур, таких как окружность и круг. Знание радиуса позволяет решать задачи по нахождению длины окружности, площади круга и других важных параметров.

Определение радиуса в математике довольно простое. Радиус — это отрезок, соединяющий центр окружности или круга с любой точкой на его границе. Он является половиной диаметра, который также проходит через центр фигуры. Радиус обычно обозначается буквой r и имеет числовое значение.

Примеры использования радиуса в математике могут помочь лучше понять его смысл и применение. Например, если нам известна длина радиуса r, мы можем найти длину окружности по формуле C = 2πr, где π — это число «пи», приближенно равное 3,14. Также радиус позволяет найти площадь круга, используя формулу S = πr². Зная радиус, можно также определить, принадлежит ли точка окружности или кругу, а также решать другие задачи, связанные с этим геометрическим понятием.

Радиус в математике 5 класс

Примеры использования радиуса в математике 5 класса:

1. Определение длины окружности. Длина окружности равна произведению числа «Пи» (π, приблизительно равно 3.14) и удвоенному радиусу: длина = 2πr.
2. Вычисление площади окружности. Площадь окружности равна произведению числа «Пи» и квадрата радиуса: площадь = πr².
3. Нахождение площади круга, ограниченного сектором. Площадь сектора равна произведению числа «Пи» и квадрата радиуса, умноженного на меру центрального угла сектора, делённую на 360: площадь сектора = (πr² * α) / 360.

Радиус играет важную роль в геометрии и позволяет решать множество задач, связанных с окружностями. Понимание и использование понятия радиуса помогает развивать логическое мышление и аналитические навыки учеников 5 класса.

Определение радиуса

Радиус обозначается буквой «r». Длина радиуса может быть разной и зависит от размера окружности. Чем больше окружность, тем длиннее радиус. Чтобы найти длину радиуса, нужно знать длину окружности или площадь круга.

Радиус используется для решения различных задач. Например, с помощью радиуса можно найти длину окружности или площадь круга. Он также используется при построении и измерении окружностей.

Зная радиус окружности, можно определить ее другие характеристики, такие как диаметр, длина окружности и площадь круга. Поэтому знание радиуса позволяет более глубоко понять свойства окружностей и использовать их при решении задач.

Радиус окружности

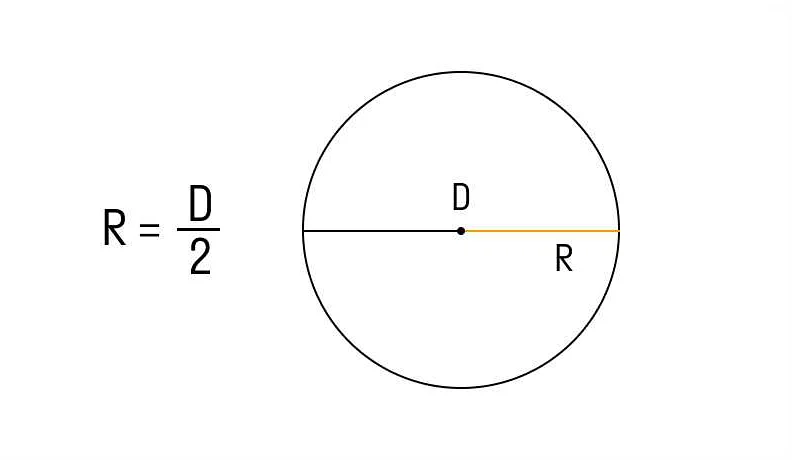
Радиус окружности является одной из основных характеристик окружности и определяет ее размер. Длина радиуса равна половине длины диаметра окружности.

Радиус окружности имеет несколько важных свойств:

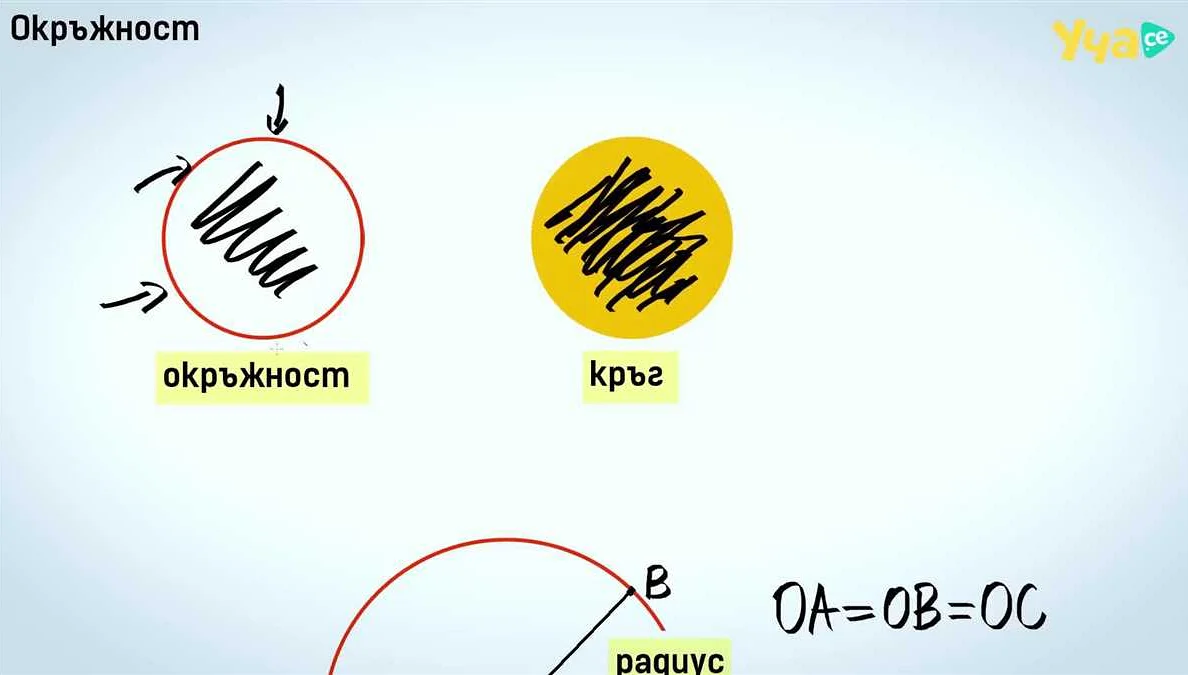
1. Радиус окружности одинаков для всех ее точек.
2. Радиус окружности является вектором, направленным от центра окружности к любой точке на ее окружности.

Зная радиус окружности, можно вычислить другие характеристики окружности, такие как ее диаметр, длина окружности и площадь.

Примеры использования радиуса окружности:

Пример 1:

Пусть радиус окружности равен 5 см. Тогда диаметр окружности будет равен 10 см, а длина окружности — 31,4 см (приближенное значение, округленное до десятых).

Пример 2:

Если радиус окружности равен 3 м, то площадь этой окружности будет равна 28,27 м2 (приближенное значение, округленное до сотых).

Радиус сферы

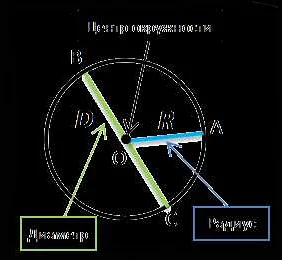
Для вычисления радиуса сферы необходимо знать диаметр сферы, который представляет собой отрезок, соединяющий две точки на сфере, проходящие через ее центр. Радиус сферы равен половине ее диаметра.

Например, если диаметр сферы равен 10 см, то радиус будет равен 5 см.

Радиус сферы используется для вычисления площади поверхности сферы и объема сферы. Формула для вычисления площади поверхности сферы: S = 4πr², где S — площадь поверхности, r — радиус сферы. Формула для вычисления объема сферы: V = (4/3)πr³, где V — объем, r — радиус сферы.

Радиус сферы также используется в геометрии и физике для решения различных задач и вычислений.

Радиус вектора

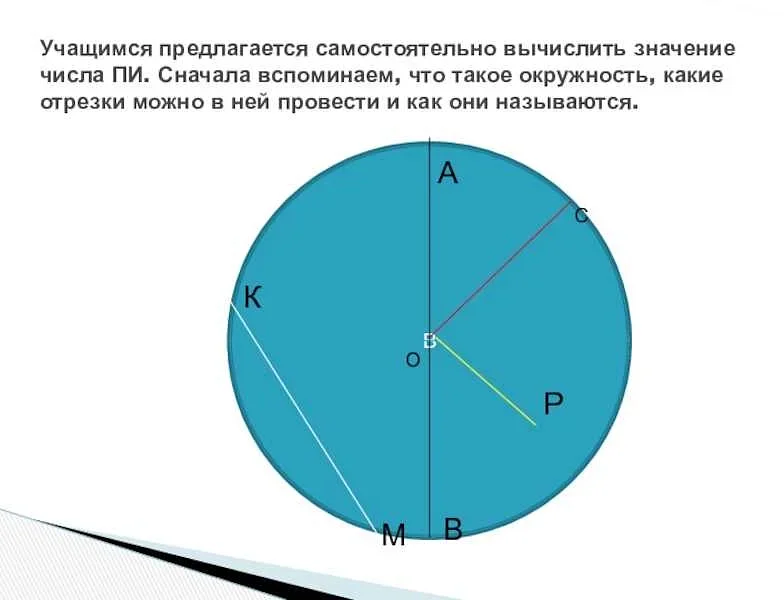
Радиус вектор является основным понятием в векторной алгебре и широко применяется в физике и геометрии. Он позволяет описывать положение точки в пространстве и осуществлять операции с векторами, такие как сложение и вычитание.

Длина радиуса вектора вычисляется по формуле:

r = √(x2 + y2)

Например, если задана точка (3, 4), то радиус вектор будет равен r = √(32 + 42) = 5.

Таким образом, радиус вектора позволяет определить длину вектора и его направление относительно начала координат.

Примеры радиуса

Ниже приведены некоторые примеры использования радиуса в математике:

1. Нахождение длины окружности: Для нахождения длины окружности необходимо умножить радиус на 2 и на число «π» (пи). Формула выглядит следующим образом: Длина окружности = 2 * π * r.
2. Нахождение площади окружности: Для нахождения площади окружности необходимо возвести радиус в квадрат и умножить на число «π» (пи). Формула выглядит следующим образом: Площадь окружности = π * r^2.
3. Нахождение площади круга: Площадь круга можно найти, используя формулу площади окружности или радиус исходя из площади круга. Формула выглядит следующим образом: Площадь круга = π * r^2.
4. Нахождение площади сектора окружности: Для нахождения площади сектора окружности необходимо умножить площадь всей окружности на отношение меры угла сектора к 360 градусам. Формула выглядит следующим образом: Площадь сектора окружности = (π * r^2 * α) / 360, где α — мера угла сектора.

Это лишь несколько примеров использования радиуса в математике. Радиус также используется в различных геометрических задачах, в тригонометрии и других областях математики.

Вычисление радиуса

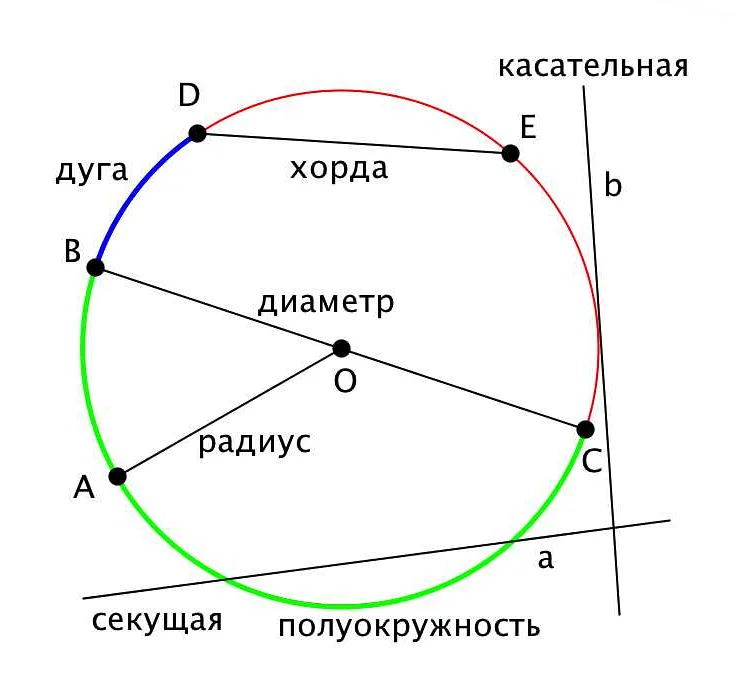
Вычисление радиуса может быть осуществлено по следующей формуле:

1. Если известна длина окружности (C), то радиус (r) можно найти по формуле: r = C / (2π), где π (пи) – это математическая константа, приближенное значение которой равно 3,14.
2. Если известна площадь круга (S), то радиус (r) можно найти по формуле: r = √(S / π).

Пример:

Допустим, у нас есть окружность с длиной равной 20 см. Чтобы найти радиус данной окружности, мы можем воспользоваться формулой r = C / (2π). Подставляя значения, получаем: r = 20 / (2 * 3,14) ≈ 3,18 см.

Таким образом, радиус этой окружности составляет примерно 3,18 см.

Свойства радиуса

У радиуса окружности есть несколько важных свойств:

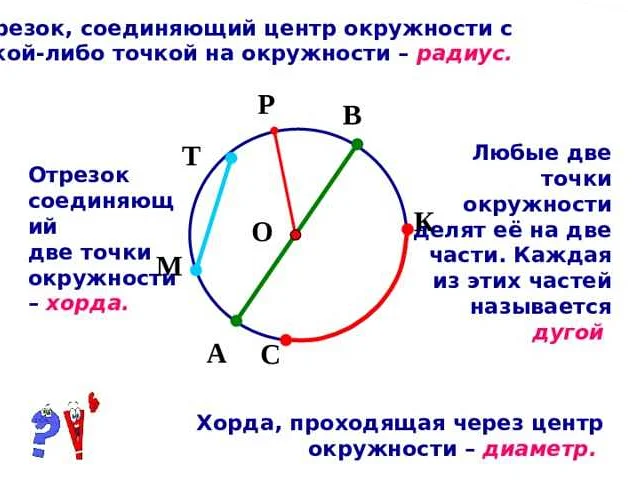
1. Радиус окружности одинаков для всех ее точек. Это означает, что отрезок, соединяющий центр окружности с любой ее точкой, будет иметь одинаковую длину.
2. Радиус является половиной диаметра окружности. Диаметр окружности – это отрезок, проходящий через центр и имеющий концы на ее окружности. Диаметр в два раза больше радиуса.
3. Радиус определяет размер окружности. Длина окружности равна удвоенному произведению числа «пи» на радиус (L = 2πr).

Например, для окружности с радиусом 5 см, диаметр будет равен 10 см, а длина окружности составит примерно 31,42 см.

Вопрос-ответ:

Что такое радиус?

В математике радиус — это отрезок, соединяющий центр окружности с любой ее точкой. Он является половиной диаметра и обозначается символом r.

Как найти радиус окружности?

Для нахождения радиуса окружности нужно разделить диаметр на 2. Если известна длина окружности, то радиус можно найти, разделив длину на 2π, где π — это математическая константа, примерно равная 3,14.

Как определить длину окружности по радиусу?

Длину окружности можно найти, используя формулу L = 2πr, где L — длина окружности, а r — радиус. Пример: если радиус равен 3 см, то длина окружности будет примерно равна 18,85 см.

Можно ли найти площадь окружности по радиусу?

Да, площадь окружности можно найти по формуле S = πr^2, где S — площадь, а r — радиус. Пример: если радиус равен 5 см, то площадь окружности будет примерно равна 78,54 см^2.

Какие еще примеры использования радиуса в математике?

Радиус используется не только для нахождения длины и площади окружности, но и для решения различных задач. Например, для нахождения площади круга, объема шара, длины дуги окружности и т. д. Радиус также используется в геометрии для определения расстояния между точками на плоскости.

Что такое радиус?

Радиус — это отрезок, соединяющий центр окружности с любой точкой на ней.

Видео по теме: