Что такое разность двух чисел в математике
Содержимое
- 1 Что такое разность двух чисел в математике
- 1.1 Разность двух чисел в математике
- 1.2 Видео по теме:
- 1.3 Что такое разность двух чисел?
- 1.4 Определение разности чисел
- 1.5 Вопрос-ответ:
- 1.6 Как вычислить разность чисел?
- 1.7 Примеры вычисления разности чисел
- 1.8 Свойства разности чисел
- 1.9 Как использовать разность чисел в реальной жизни?
- 1.10 Важность понимания понятия разности чисел
Разность двух чисел в математике это результат вычитания одного числа из другого. Узнайте как вычислить разность чисел и как она используется в математических операциях.
Разность двух чисел в математике является одной из основных операций арифметики. Она позволяет нам вычислить, насколько одно число отличается от другого. Разность можно рассматривать как «потерю» или «прибавление» определенного количества.
Для вычисления разности двух чисел необходимо первое число вычесть из второго. Если первое число больше второго, то разность будет отрицательной. Если первое число меньше второго, то разность будет положительной. Если числа равны, то разность будет равна нулю.
Например, если у нас есть два числа: 5 и 3, то разность будет равна 2. В этом случае мы вычитаем 3 из 5 и получаем 2. Если бы у нас были числа 3 и 5, то разность была бы -2. Также, если у нас были бы числа 5 и 5, то разность составила бы 0.
Разность двух чисел может быть полезна во многих ситуациях. Например, она может помочь нам вычислить изменение значения величины, узнать насколько одно число больше (или меньше) другого, или решить задачу на нахождение неизвестного числа.
Разность двух чисел в математике
Разность двух чисел в математике представляет собой результат вычитания одного числа из другого. Она показывает, насколько одно число отличается от другого.
Для вычисления разности двух чисел нужно первое число уменьшить на второе. Если первое число больше второго, то результат будет положительным числом. Если же первое число меньше второго, то разность будет отрицательной.
Например, если у нас есть числа 8 и 5, то разность будет равна 3 (8 — 5 = 3). Если же у нас есть числа 5 и 8, то разность будет равна -3 (5 — 8 = -3).
Разность двух чисел может использоваться для решения различных задач и проблем, например, для вычисления изменения величины или расстояния между двумя точками.
В математике разность двух чисел обозначается символом «-«, который ставится между числами, вычитаемыми друг из друга.
Знание и понимание понятия разности чисел является важной частью базовых математических навыков и может быть полезно в повседневной жизни и в решении различных задач.
Видео по теме:
Что такое разность двух чисел?
Чтобы найти разность двух чисел, нужно из большего числа вычесть меньшее число. Например, разность чисел 9 и 5 равна 4, так как 9 — 5 = 4.
Разность чисел может быть как положительной, так и отрицательной. Если первое число больше второго, то разность будет положительной. Например, разность чисел 8 и 3 равна 5, так как 8 — 3 = 5.
Если первое число меньше второго, то разность будет отрицательной. Например, разность чисел 4 и 7 равна -3, так как 4 — 7 = -3.
Разность чисел может быть нулевой, если оба числа равны. Например, разность чисел 6 и 6 равна 0, так как 6 — 6 = 0.
Определение разности чисел
Для вычисления разности нужно вычесть из большего числа меньшее число. Например, если у нас есть числа 7 и 3, то разность между ними будет равна 7 — 3 = 4.
Разность чисел может быть как положительной, так и отрицательной. Если первое число больше второго, то разность будет положительной. Если же первое число меньше второго, то разность будет отрицательной. Например, разность чисел -3 и 5 равна -3 — 5 = -8.
Разность чисел имеет свойства коммутативности и ассоциативности. Коммутативность означает, что порядок чисел в выражении не влияет на результат разности. Ассоциативность означает, что при наличии нескольких вычитаний можно выполнить их в любом порядке без изменения результата.
Разность чисел удобно использовать в различных ситуациях, например при измерении изменений, расчете долгов, определении превышения одного значения над другим и т.д.
Вопрос-ответ:
Что такое разность двух чисел?
Разность двух чисел — это результат вычитания одного числа из другого. Это показывает, насколько одно число меньше или больше другого.
Как найти разность двух чисел?
Для того чтобы найти разность двух чисел, нужно вычесть одно число из другого. Например, чтобы найти разность между числами 8 и 3, нужно вычесть 3 из 8, получив таким образом 5.
Можно ли разность двух чисел выразить с помощью алгоритма?
Да, разность двух чисел можно выразить с помощью алгоритма. Алгоритм вычитания состоит из последовательного вычитания цифр чисел, начиная с самых правых разрядов, и переноса единицы, если необходимо.
Какие примеры можно привести для лучшего понимания понятия разности двух чисел?
Примеры разности двух чисел: разность между 10 и 5 равна 5, разность между 15 и 10 равна 5, разность между -3 и -7 равна 4. Это примеры, которые помогут лучше понять понятие разности двух чисел.
Какая разность будет, если одно из чисел отрицательное?
Если одно из чисел отрицательное, то разность будет зависеть от знака чисел. Если отрицательное число больше по модулю, чем положительное, то разность будет отрицательной. Если положительное число больше по модулю, чем отрицательное, то разность будет положительной. Например, разность между -5 и 3 будет равна -8, а разность между 5 и -3 будет равна 8.
Как вычислить разность чисел?
Для вычисления разности двух чисел необходимо выполнить следующие действия:
- Возьмите первое число и вычтите из него второе число. Например, если первое число равно 10, а второе число равно 5, то разность будет равна 10 — 5 = 5.
- Если вычисляемая разность отрицательна, то перед результатом ставится знак минус («-«). Например, если первое число равно 5, а второе число равно 10, то разность будет равна 5 — 10 = -5.
Вычисление разности чисел в математике является одной из основных операций и может применяться в различных сферах, например, для определения изменения значений, вычисления расстояний и многих других задач.
Примеры вычисления разности чисел
Разность двух чисел можно вычислить, вычитая из большего числа меньшее число. Вот несколько примеров:
Первое числоВторое числоРазность
| 10 | 5 | 10 — 5 = 5 |
| 15 | 7 | 15 — 7 = 8 |
| 20 | 12 | 20 — 12 = 8 |
Таким образом, разность чисел является результатом вычитания одного числа из другого и показывает, насколько они отличаются друг от друга.
Свойства разности чисел

Свойства разности чисел позволяют упростить вычисления и использовать определенные правила при работе с этой операцией.
Свойства разности чисел:
1. Коммутативное свойство: порядок вычитаемых чисел не влияет на результат. То есть, разность чисел a и b равна разности чисел b и a. Например: если a = 5 и b = 3, то a — b = 5 — 3 = 2, и b — a = 3 — 5 = -2.
2. Ассоциативное свойство: при вычитании трех чисел, результат не зависит от того, какие числа сначала вычли. То есть, разность чисел a, b и c будет одинаковой, независимо от порядка вычитания. Например: если a = 10, b = 4 и c = 2, то (a — b) — c = (10 — 4) — 2 = 4 — 2 = 2, и a — (b — c) = 10 — (4 — 2) = 10 — 2 = 8.
3. Нулевое свойство: разность числа и нуля равна самому числу. То есть, если a – любое число, то a — 0 = a. Например: если a = 7, то a — 0 = 7 — 0 = 7.
4. Свойство суммы: разность суммы двух чисел и третьего числа равна разности первого числа и разности второго и третьего чисел. То есть, если a, b и c – любые числа, то (a + b) — c = a — (c — b). Например: если a = 8, b = 5 и c = 3, то (8 + 5) — 3 = 13 — 3 = 10, и 8 — (3 — 5) = 8 — (-2) = 10.
Эти свойства помогают упростить вычисления и сделать работу с разностью чисел более удобной.
Как использовать разность чисел в реальной жизни?
1. Финансы:
Разность чисел может быть полезна при учете финансов и планировании бюджета. Например, если у вас есть определенный доход и вы хотите знать, сколько денег останется после вычета расходов, вы можете вычислить разность между доходом и расходами.
2. Торговля:
Разность чисел может быть использована в торговле для определения прибыли или убытка. Если вы купили товары по определенной цене и продали их по другой цене, разность между этими двумя ценами покажет вашу прибыль или убыток.
3. Учет запасов:
Разность чисел может быть полезна при учете запасов товаров или материалов. Если вы знаете, сколько товаров было на складе в начале периода и сколько товаров было на складе в конце периода, вы можете вычислить разность между этими двумя значениями и узнать, сколько товаров было продано или использовано.
4. Измерение изменений:
Разность чисел может быть использована для измерения изменений в различных величинах. Например, если вы хотите узнать, насколько выросли или уменьшились продажи за определенный период, вы можете вычислить разность между значениями продаж в начале и конце периода.
Таким образом, разность чисел является полезным инструментом для решения различных задач и применяется во многих сферах жизни, от финансов до учета запасов и измерения изменений.
Важность понимания понятия разности чисел

Понимание разности чисел играет важную роль в решении различных задач, как в повседневной жизни, так и в научных и технических областях. Например, при покупке товаров с помощью разности чисел можно определить, сколько денег останется у покупателя после оплаты. В науке и технике понятие разности чисел используется для измерения различных величин, а также для определения изменений в этих величинах.
Понимание понятия разности чисел также помогает развивать абстрактное мышление и логическое мышление. Решение задач на вычитание требует умения анализировать информацию, применять математические операции и делать выводы. Это помогает развивать способность к анализу, рассуждению и принятию решений.
Поэтому важно уделить внимание изучению понятия разности чисел, чтобы иметь возможность применять его в различных ситуациях и решать задачи, требующие математического мышления и логики.

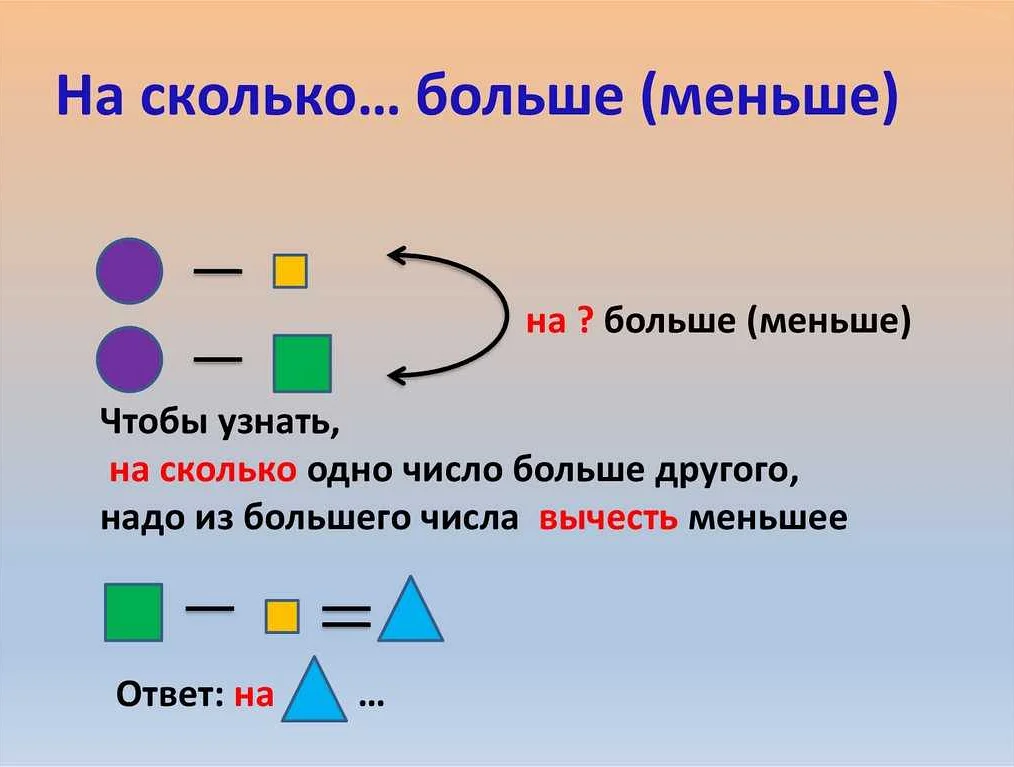

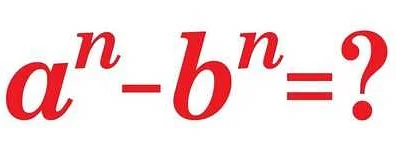
Разность двух чисел в математике — это результат вычитания одного числа из другого. Определение этого понятия может показаться очень простым, но на самом деле оно играет важную роль в решении различных задач. Давайте рассмотрим пример, чтобы лучше понять, как работает разность. Представьте, что у вас есть 10 яблок, и вы отдаете 3 яблока своему другу. Чтобы вычислить, сколько яблок останется у вас, вы должны вычесть 3 из 10. Результатом будет 7, что означает, что у вас останется 7 яблок. Таким образом, разность двух чисел позволяет нам найти количество, которое остается после вычитания. Это очень полезно при решении задач на поиск недостающих значений или при вычислении изменений величин. Использование математической операции вычитания позволяет нам легко определить разность между двумя числами и применить это знание в повседневной жизни. Например, при покупке товаров мы можем вычислить разность между ценой товара и нашим бюджетом, чтобы знать, сколько денег нам необходимо еще найти или сколько нам останется после покупки. Таким образом, понимание понятия разности чисел в математике является важным навыком, который поможет нам решать различные задачи в повседневной жизни.
Разность двух чисел — это результат вычитания одного числа из другого. Это основное понятие в математике, которое помогает нам измерять изменения и сравнивать значения. Например, если у нас есть числа 10 и 5, разность между ними будет равна 5. Это означает, что одно число больше другого на 5. Разность часто используется для определения изменений величин, таких как доходы, расходы или температура. Например, если температура сегодня -5 градусов, а вчера было +5 градусов, разность между ними составит -10 градусов, что означает, что температура сегодня на 10 градусов ниже, чем вчера. Понимание понятия разности двух чисел позволяет нам более точно анализировать и интерпретировать числовые данные в различных сферах нашей жизни.
Очень интересная статья! Я всегда задавался вопросом, что такое разность двух чисел в математике, и наконец-то нашел ответ. Понятно объяснено, что разность — это результат вычитания одного числа из другого. Теперь я знаю, как правильно рассчитывать разность и какую операцию использовать. Примеры, приведенные в статье, также помогли мне лучше понять эту концепцию. Теперь мне кажется, что разность чисел — это нечто простое и доступное. Я уверен, что этот материал будет полезен как начинающим, так и тем, кто уже знаком с основами математики. Большое спасибо автору! Я буду рекомендовать эту статью своим друзьям, которые тоже хотят узнать больше о разности чисел.