Что такое разность и произведение в математике

Разность и произведение — основные арифметические операции в математике. Разность обозначает разницу между двумя числами, а произведение — их умножение. Узнайте, как выполнять эти операции и как они применяются в решении математических задач.

В математике существует множество основных арифметических операций, которые позволяют нам решать различные задачи и выполнять вычисления. Две из таких операций — разность и произведение — широко применяются в повседневной жизни и научных исследованиях.

Разность — это операция, которая позволяет нам вычислить разницу между двумя числами. Обозначается она знаком минус (-) между числами, например, 5 — 2. Результат разности показывает, насколько одно число меньше или больше другого. Например, если вычесть из числа 5 число 2, получится разность равная 3.

Произведение — это операция, которая позволяет нам найти результат умножения двух чисел. Обозначается знаком умножения (×) или знаком точки (·) между числами, например, 5 × 2 или 5 · 2. Результат произведения показывает, сколько раз одно число содержится в другом. Например, если умножить число 5 на число 2, получится произведение равное 10.

Разность и произведение имеют свои основные принципы и правила, соблюдение которых позволяет выполнять точные вычисления и получать корректные результаты. Например, при вычислении разности нужно помнить о знаке минус и его влиянии на результирующее число. Также при умножении важно помнить о коммутативности операции и ее свойствах, которые позволяют изменять порядок сомножителей без изменения результата.

Знание понятия разности и произведения в математике является основой для более сложных операций и концепций, таких как деление, степень и корень. Понимание этих операций позволяет нам анализировать и решать различные задачи, а также использовать математические методы в научных исследованиях и повседневной жизни.

Разность и произведение в математике: понятие, определение и основные принципы

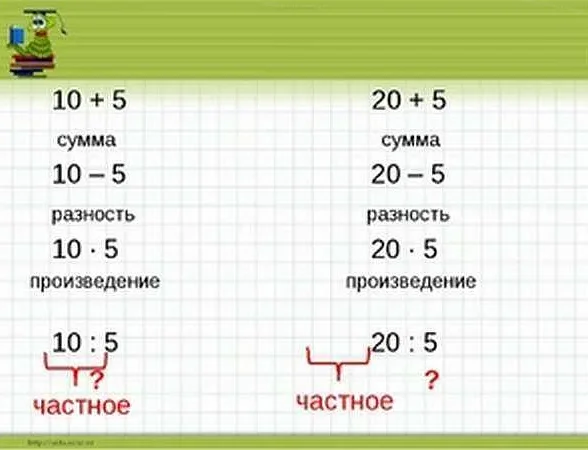
Разность двух чисел определяется как результат вычитания одного числа из другого. Если у нас есть числа a и b, то разность обозначается как a — b. Разность может быть положительной, отрицательной или нулевой в зависимости от значений a и b. Если a больше b, то разность будет положительной, если a меньше b, то разность будет отрицательной, а если a равно b, то разность будет равна нулю.

Произведение двух чисел определяется как результат умножения этих чисел. Если у нас есть числа a и b, то произведение обозначается как a * b. Произведение может быть положительным, отрицательным или нулевым в зависимости от значений a и b. Если оба числа a и b положительные или отрицательные, то произведение будет положительным. Если одно из чисел a или b отрицательное, то произведение будет отрицательным. Если одно из чисел равно нулю, то произведение будет равно нулю.

Основные принципы разности и произведения в математике следующие:

ОперацияПринцип

Разность	Разность двух чисел равна сумме первого числа и противоположного второго числа.
Произведение	Произведение двух чисел равно сумме первого числа, взятого нужное количество раз.

Например, разность чисел 5 и 3 равна 2, так как 5 — 3 = 2. Произведение чисел 2 и 4 равно 8, так как 2 * 4 = 8.

Разность и произведение являются важными операциями в математике и используются в различных областях, включая алгебру, геометрию и физику. Они позволяют решать задачи, моделировать явления и строить математические модели.

Разность и произведение: общая суть

Разность может быть найдена путем вычитания одного числа (вычитаемого) из другого числа (уменьшаемого). Например, если у нас есть числа 5 и 3, разность будет равна 2 (5 — 3 = 2). Разность может быть положительной, отрицательной или нулевой в зависимости от значений чисел.

Произведение, с другой стороны, представляет собой операцию умножения двух чисел. Например, если мы умножим числа 4 и 2, получим произведение 8 (4 * 2 = 8). Произведение также может быть положительным, отрицательным или равным нулю.

Разность и произведение используются во многих областях математики и имеют важное значение для понимания и решения различных задач. Они являются основными операциями в арифметике и играют важную роль в алгебре, геометрии и других разделах математики.

Понимание сути разности и произведения помогает нам более глубоко изучать и использовать математические концепции и решать сложные задачи. Они являются фундаментальными понятиями, которые позволяют нам работать с числами и их свойствами.

Разность: определение и примеры

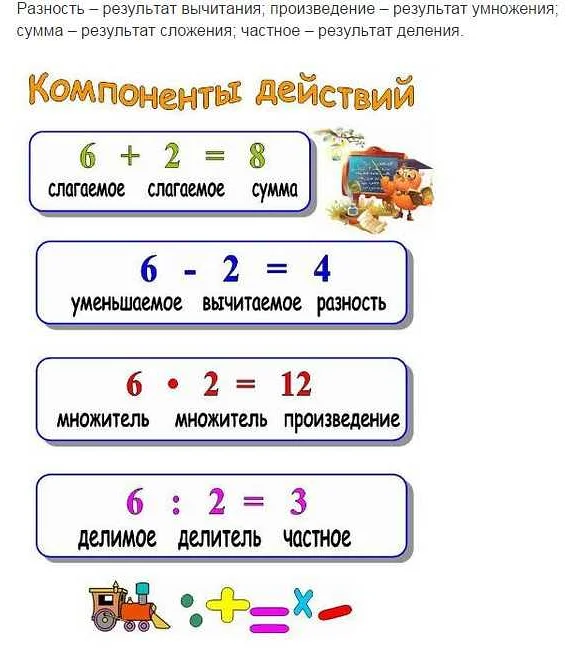
Для нахождения разности двух чисел, необходимо из большего числа вычесть меньшее число. Например, разность чисел 9 и 5 равна 4, так как 9 — 5 = 4.

Также разность может быть отрицательной, если первое число меньше второго. Например, разность чисел 5 и 9 равна -4, так как 5 — 9 = -4. В этом случае отрицательное значение указывает на то, что первое число находится перед вторым числом на числовой оси.

Разность может быть применима не только к целым числам, но и к дробям и десятичным числам. Например, разность дробей 3/4 и 1/2 равна 1/4, так как 3/4 — 1/2 = 1/4.

Также можно вычислять разность переменных или выражений. Например, разность выражений 2x и x равна x, так как (2x — x) = x.

Разность является одной из основных операций в математике и имеет множество применений в различных областях, включая алгебру, геометрию и физику.

Произведение: определение и свойства

Произведение двух чисел a и b равно их умножению и обозначается a × b или a * b. В результате выполнения произведения получается новое число, называемое произведением. Например, произведение чисел 2 и 3 равно 6.

Произведение обладает рядом свойств:

1. Ассоциативность: при умножении трех и более чисел результат не зависит от порядка выполнения операций. Например, (a × b) × c = a × (b × c).
2. Коммутативность: порядок множителей не влияет на результат произведения. Например, a × b = b × a.
3. Свойство нуля: произведение числа на ноль всегда равно нулю. Например, a × 0 = 0.
4. Свойство единицы: произведение числа на единицу равно самому числу. Например, a × 1 = a.
5. Распределительное свойство: произведение суммы двух чисел равно сумме произведений каждого числа с одним и тем же множителем. Например, (a + b) × c = a × c + b × c.

Произведение используется во многих областях математики, физики, экономики и других науках. Оно позволяет вычислять площади, объемы, находить проценты, моделировать процессы роста и многое другое.

Арифметическая разность и произведение

Арифметическая разность — это операция вычитания одного числа из другого. Разность двух чисел можно найти, вычитая из большего числа меньшее число. Например, разность чисел 7 и 3 равна 4 (7 — 3 = 4).

Пример: Вычислить разность чисел 10 и 5.

Решение: Разность чисел 10 и 5 равна 5 (10 — 5 = 5).

Арифметическое произведение — это операция умножения двух чисел. Произведение чисел можно найти, умножая одно число на другое. Например, произведение чисел 4 и 3 равно 12 (4 × 3 = 12).

Пример: Вычислить произведение чисел 8 и 2.

Решение: Произведение чисел 8 и 2 равно 16 (8 × 2 = 16).

Арифметическая разность и произведение широко применяются в различных областях математики, физики, экономики и научных исследованиях. Они помогают решать задачи, связанные с вычислениями и моделированием различных явлений и процессов.

Геометрическая разность и произведение

Геометрическая разность и произведение являются специфическими видами операций, которые связаны с геометрическими объектами. Геометрическая разность двух чисел представляет собой расстояние между двумя точками на числовой оси. Умножение также имеет геометрическую интерпретацию, которая связана с понятием площади прямоугольника.

Для наглядного представления геометрической разности и произведения, часто используется таблица, в которой числа располагаются в виде координат на плоскости. Такая таблица называется графиком чисел.

ЧислоГеометрическое представление

5	●●●●●
2	●●
3	●●●

В данной таблице числа представлены в виде точек, где каждая точка соответствует одному числу. Геометрическая разность между числами 5 и 2 равна 3, что соответствует расстоянию между точками на числовой оси. Геометрическое представление произведения двух чисел может быть связано с площадью прямоугольника, построенного на основе этих чисел.

Таким образом, геометрическая разность и произведение позволяют нам визуализировать и понять числа и их взаимосвязь на геометрическом уровне.

Математические операции: разность и произведение

Разность — это операция, которая позволяет найти разницу между двумя числами. Чтобы найти разность, нужно от одного числа отнять другое. Например, для чисел 5 и 3 разность будет равна 2.

Формула для нахождения разности:

Разность = Первое число — Второе число

Произведение — это операция, которая позволяет найти произведение двух чисел. Чтобы найти произведение, нужно умножить одно число на другое. Например, произведение чисел 4 и 6 будет равно 24.

Формула для нахождения произведения:

Произведение = Первое число * Второе число

Разность и произведение являются основными операциями в математике и широко используются в решении различных задач. Понимание этих операций позволяет выполнять различные вычисления и анализировать числовые данные.

Практическое применение: разность и произведение

Прежде всего, понимание и использование понятий разности и произведения необходимы в повседневных финансовых расчетах. Например, при составлении бюджета или ведении бухгалтерии разность может использоваться для определения разницы между доходами и расходами. Произведение, в свою очередь, может применяться для расчета общей стоимости покупки или для определения процента скидки.

В науке и инженерии также широко используются операции разности и произведения. Например, при решении физических задач разность может использоваться для определения изменения какой-либо величины во времени, а произведение – для расчета площади поверхности или объема объекта.

Разность и произведение также играют важную роль в компьютерной науке и программировании. Операции вычитания и умножения используются для решения задач по обработке данных, алгоритмическому программированию и созданию математических моделей.

В целом, понимание и умение использовать операции разности и произведения является неотъемлемой частью математической грамотности и является основой для решения разнообразных задач в различных сферах деятельности.

Видео по теме:

Что такое разность в математике?

Разность в математике — это результат вычитания одного числа из другого. Другими словами, это значение, которое получается, когда мы вычитаем одно число из другого.

Как определить произведение двух чисел?

Произведение двух чисел — это результат умножения этих чисел. Для того чтобы найти произведение двух чисел, нужно умножить первое число на второе число.

Можно ли вычислить разность и произведение не только чисел, но и других математических объектов?

Да, разность и произведение можно вычислять не только для чисел, но и для других математических объектов, таких как многочлены, матрицы и т.д. Принципы вычисления разности и произведения для этих объектов могут отличаться от принципов вычисления для чисел, но в основе все равно лежит понятие разности и произведения.

Какие основные принципы лежат в основе вычисления разности?

Основные принципы вычисления разности включают в себя вычитание одного числа из другого, приоритет операций (сначала вычитание, затем сложение), и свойства операции вычитания (ассоциативность, коммутативность и др.). Также важно учитывать знаки чисел при вычитании.

Какие свойства произведения чисел можно выделить?

Свойства произведения чисел включают в себя коммутативность (порядок множителей не влияет на результат), ассоциативность (порядок умножения не влияет на результат), дистрибутивность (произведение суммы равно сумме произведений) и тождественность (умножение на единицу не меняет число). Также важно учитывать знаки чисел при умножении.

Как определить разность чисел?

Разность чисел определяется путем вычитания одного числа из другого. Например, разность чисел 5 и 3 равна 2, так как 5 — 3 = 2.