Что такое re в математике

Re в математике является аббревиатурой от слова

В математике термин «re» обозначает множество действительных чисел. Действительные числа включают в себя все рациональные числа (которые могут быть представлены в виде дробей) и иррациональные числа (которые не могут быть представлены в виде дроби и имеют бесконечное количество десятичных знаков).

Символ «re» происходит от слова «realis», что в переводе с латыни означает «реальный». Он используется для обозначения множества чисел, которые могут быть представлены на числовой оси и фактически существуют в реальном мире.

Примеры использования множества чисел re в математике включают решение уравнений, графики функций, анализ данных и многое другое. Действительные числа являются основой для многих математических концепций и приложений, и их понимание позволяет нам более глубоко изучать и анализировать окружающий мир.

Например, при решении уравнения x^2 = 9, мы можем использовать множество действительных чисел re, чтобы найти все значения x, которые удовлетворяют данному уравнению. В этом случае, x = 3 и x = -3 являются решениями уравнения, поскольку 3^2 = 9 и (-3)^2 = 9.

Использование множества чисел re в математике позволяет нам решать разнообразные задачи, моделировать реальные ситуации и исследовать различные аспекты количественных явлений. Понимание этого понятия помогает нам строить более точные модели, прогнозировать результаты и принимать обоснованные решения на основе анализа данных и числовых фактов.

Определение re в математике

Математические объекты, представленные в виде множеств, могут быть числами, символами, буквами, фигурами, функциями и т.д. Все элементы в множестве должны быть уникальными — каждый элемент может входить в множество только один раз.

Множества в математике часто обозначаются заглавными буквами латинского алфавита, например: A, B, C и т.д. Когда требуется указать, что элементы множества принадлежат определенной области или условию, используются дополнительные обозначения и символы.

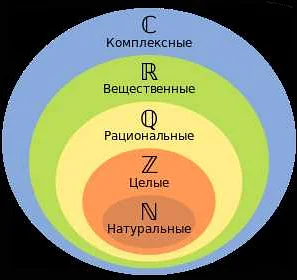
Например, множество натуральных чисел можно обозначить как ℝ, а множество целых чисел как ℤ. Множество всех действительных чисел обычно обозначается как ℝ или R.

Примеры использования множеств в математике включают операции объединения, пересечения, разности, декартового произведения, а также понятия подмножества и равенства множеств. Множества являются основным понятием в теории множеств и играют важную роль в различных областях математики, включая алгебру, анализ, комбинаторику, теорию вероятности и др.

Примеры использования re в математике

Регулярные выражения (re) широко применяются в математике для работы с текстами и строками. Вот несколько примеров использования re в математике:

1. Поиск чисел в тексте: re можно использовать для поиска чисел в строке. Например, можно найти все числа в тексте и произвести с ними дальнейшие вычисления.
2. Проверка формата даты: re может быть использовано для проверки правильности формата даты. Например, можно проверить, соответствует ли заданная строка формату ГГГГ-ММ-ДД.
3. Поиск и замена текста: re можно использовать для поиска определенного текста и его замены на другой текст. Например, можно заменить все вхождения определенного слова в тексте на другое слово.
4. Проверка правильности ввода: re может быть использовано для проверки правильности ввода данных. Например, можно проверить, соответствует ли заданная строка определенному формату (например, адрес электронной почты).
5. Разделение текста на части: re можно использовать для разделения текста на части по определенному разделителю. Например, можно разделить строку на слова или предложения.

Это только несколько примеров использования re в математике. Регулярные выражения предоставляют мощный инструмент для работы с текстами и строками, и их применение может быть очень широким и разнообразным.

Роль re в решении уравнений

Модуль re (регулярные выражения) в математике играет важную роль в решении уравнений. Он позволяет осуществлять поиск и манипуляции с текстовыми данными, которые представляют собой уравнения. Используя регулярные выражения, можно находить шаблоны и сопоставлять их с уравнениями, что дает возможность выполнять различные операции, включая решение уравнений.

Например, рассмотрим уравнение:

2x + 3 = 7

С помощью модуля re можно определить шаблон, который соответствует этому уравнению. Например, шаблон «(\d+)x\s*\+\s*(\d+)\s*=\s*(\d+)» будет соответствовать уравнению, где \d+ обозначает любую последовательность цифр, \s* — любое количество пробелов.

После того как шаблон определен, можно использовать регулярные выражения для извлечения значений коэффициентов и свободного члена уравнения:

• Коэффициент при x: группа 1
• Коэффициент перед знаком «+»: группа 2
• Значение справа от знака «=»: группа 3

Таким образом, используя модуль re, можно извлечь значения коэффициентов и свободного члена уравнения, а затем применить соответствующие математические операции для решения уравнения.

Регулярные выражения являются мощным инструментом для работы с текстом и находят применение во многих областях, включая математику и решение уравнений.

Практическое применение re в физике

Re вычисляется как отношение инерционных сил к вязким силам в течении. Оно определяется формулой:

Re = ρvL/η

где ρ — плотность жидкости или газа, v — скорость течения, L — характерный размер объекта, а η — динамическая вязкость среды.

Re имеет большое значение при изучении течения жидкости или газа в различных условиях. Например, при малых значениях Re (Re < 2000) течение считается ламинарным, то есть плавное и предсказуемое. При больших значениях Re (Re > 4000) течение становится турбулентным, то есть хаотичным и непредсказуемым.

Применение Re в физике позволяет улучшить понимание течения жидкости или газа в различных системах. Оно используется для изучения аэродинамики, гидродинамики, теплообмена и других процессов.

Например, при проектировании автомобилей или самолетов, знание значения Re позволяет определить оптимальную форму крыла или обтекателя, чтобы минимизировать сопротивление и улучшить аэродинамические характеристики.

В медицине Re применяется для изучения течения крови в сосудах. Знание значения Re позволяет определить вероятность возникновения тромбов или образования вихрей, что помогает разработать эффективные методы лечения и профилактики.

Таким образом, практическое применение Re в физике позволяет улучшить проектирование различных систем и процессов, а также разработать эффективные методы исследования и лечения.

Производные и интегралы с использованием re

Модуль re в математике включает в себя функции и методы для работы с регулярными выражениями. Он позволяет нам искать и сопоставлять шаблоны в строках, что может быть очень полезно при работе с производными и интегралами.

Регулярные выражения используются для поиска и обработки текста с определенным шаблоном. Они позволяют нам искать и извлекать различные фрагменты информации из строк, что может быть полезно при работе с математическими выражениями.

Например, мы можем использовать регулярное выражение для поиска всех переменных в математическом выражении и замены их на соответствующие значения. Это может быть полезно при вычислении производных и интегралов.

Кроме того, модуль re позволяет нам выполнять различные операции над строками, такие как замена подстроки, разделение строки на подстроки и многое другое. Все это может быть очень полезно при работе с математическими выражениями.

Таким образом, использование модуля re в математике позволяет нам эффективно работать с производными и интегралами, а также с другими математическими выражениями. Он предоставляет нам мощные инструменты для обработки текста и выполнения различных операций над строками.

re в комплексных числах

Действительная часть комплексного числа z обозначается как Re(z) или просто re. Она представляет собой число a и соответствует координате x на комплексной плоскости.

Например, если комплексное число z = 3 + 2i, то его действительная часть равна Re(z) = 3.

Действительная часть комплексного числа позволяет определить его положение на комплексной плоскости относительно оси x.

Знание действительной части комплексного числа позволяет решать различные задачи в математике и физике, такие как нахождение корней комплексных чисел, решение уравнений и многое другое.

Применение re в теории вероятностей

В теории вероятностей символ «re» часто используется для обозначения некоторых статистических величин, таких как среднее значение, дисперсия и ковариация.

Например, среднее значение вероятности события A может быть обозначено как re(A), где A — событие, а re(A) — его среднее значение. Для дискретных случайных величин среднее значение может быть вычислено как сумма произведений значений величины на их вероятности, а для непрерывных случайных величин — как интеграл от произведения значения величины на ее плотность вероятности.

Дисперсия случайной величины X обозначается как re(X^2) — re(X)^2, где re(X) — среднее значение величины X. Дисперсия показывает меру разброса значений случайной величины относительно ее среднего значения.

Ковариация между двумя случайными величинами X и Y обозначается как re(XY) — re(X)re(Y), где re(X) и re(Y) — средние значения величин X и Y. Ковариация показывает степень линейной зависимости между двумя величинами.

Таким образом, использование символа «re» в теории вероятностей позволяет компактно обозначать основные характеристики случайных величин и описывать их статистические свойства.

Вопрос-ответ:

Что такое re в математике?

Термин «re» в математике обозначает вещественное число или множество вещественных чисел. Вещественные числа включают в себя все десятичные числа, как целые, так и дробные, а также иррациональные числа, такие как корень квадратный из двух. Множество вещественных чисел обозначается символом ℝ.

Можете привести пример использования re в математике?

Конечно! Например, если у вас есть уравнение вида x² + 2x + 1 = 0, то вы можете использовать понятие «re» для указания, что решением этого уравнения является действительное число. В данном случае, решением будет -1.

Как связаны re и комплексные числа?

Re является частью комплексных чисел. Комплексное число может быть представлено в виде a + bi, где a и b — это вещественные числа, а i — мнимая единица. Если мы хотим обозначить только вещественную часть комплексного числа, мы можем использовать «re». Например, если у нас есть комплексное число z = 3 + 4i, то re(z) = 3.

Какая связь между re и имагинарной частью комплексного числа?

Re и имагинарная часть комплексного числа являются взаимно дополняющими. Если у нас есть комплексное число z = a + bi, то re(z) + im(z) = a + bi. То есть, сумма вещественной и мнимой частей комплексного числа равна самому комплексному числу.

Могу ли я использовать re для обозначения комплексной части числа?

Нет, «re» используется исключительно для обозначения вещественной части комплексного числа. Для обозначения комплексной части числа используется «im».

Что такое re в математике?

В математике re (англ. real part) обозначает действительную часть комплексного числа. Действительная часть — это число, которое получается, если от комплексного числа отбросить мнимую часть. Например, если у нас есть комплексное число z = 3 + 2i, то его действительная часть равна 3.

Каким образом можно использовать re в математике?

re в математике может быть использовано для различных целей. Например, для вычисления действительной части комплексного числа, для анализа и построения графиков функций, содержащих комплексные числа, для решения уравнений и систем уравнений с комплексными коэффициентами и т. д. Также re может быть использовано для определения симметрии функций относительно действительной оси.

re в компьютерных науках

С помощью re можно выполнять различные операции над текстом, такие как поиск подстрок, замена текста, разделение строк на подстроки и многое другое. Он основан на использовании специальных символов и синтаксиса, которые позволяют создавать гибкие и мощные шаблоны для обработки текста.

Примеры использования re в компьютерных науках включают: валидацию ввода пользователя веб-форм, поиск и фильтрацию данных в базах данных, анализ и обработку текстовых файлов, создание лексического анализатора для компиляторов и многое другое.

Видео по теме: