Что такое s пов в математике

S-пов поверхности в математике — это специальный класс поверхностей, которые могут быть описаны уравнением вида Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0. Они играют важную роль в геометрии и алгебре и используются для решения различных задач и проблем. Узнайте больше о S-пов поверхностях и их свойствах в нашей статье.

С-пов — это одно из ключевых понятий в математике, которое используется для описания относительных позиций и взаимодействий между точками, плоскостями и пространствами. Оно является основой для решения множества задач и проблем в различных областях науки, включая геометрию, физику и компьютерную графику.

С-пов представляет собой математическую абстракцию, которая описывает относительные расположения и ориентации объектов в пространстве. Оно может быть задано в виде набора координат или в форме уравнений, которые определяют положение и форму объектов относительно друг друга.

Примеры использования с-пов в математике включают нахождение пересечений и расстояний между объектами, определение плоскостей и поверхностей, а также моделирование и визуализацию трехмерных объектов. Они также применяются в компьютерной графике для создания трехмерных сцен и анимаций.

С-пов играют важную роль в решении широкого спектра проблем, связанных с пространственной геометрией и моделированием объектов. Их использование позволяет упростить и улучшить процесс анализа и визуализации данных, а также создать реалистичные и эффективные компьютерные модели.

Определение s-пов

С-пов является особой формой поверхности, поскольку все точки на ней находятся на одинаковом расстоянии от центра. Из-за этого свойства с-пов имеет форму сферы, которая является одной из наиболее известных геометрических фигур.

С-пов можно рассматривать как трехмерный аналог окружности в двумерном пространстве. Вместо того, чтобы быть линией, как окружность, с-пов представляет собой поверхность, охватывающую все точки, находящиеся на определенном расстоянии от центра.

В математике и физике с-пов широко используется для моделирования и анализа различных явлений. Например, с-пов используется в геодезии для описания Земли и расчета ее формы и размеров. Они также используются в физике для описания распределения силы и энергии в пространстве.

Видео по теме:

Примеры использования s-пов в математике

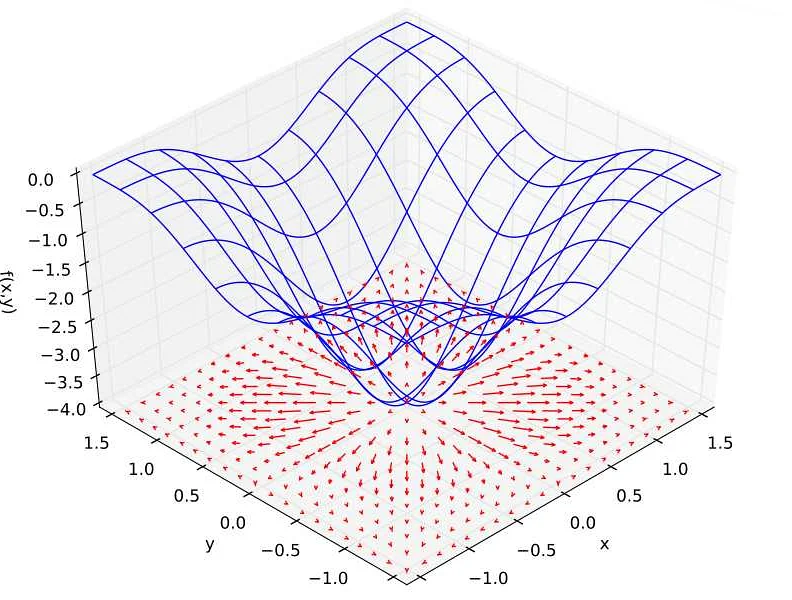
2. В математическом анализе s-повы используются для определения интеграла функции. Они позволяют вычислить площадь под графиком функции, а также найти точку, в которой происходит смена знака функции.

3. В линейной алгебре s-повы используются для решения систем линейных уравнений. Они позволяют найти такие значения переменных, при которых все уравнения системы выполняются одновременно.

4. S-повы также находят применение в теории графов. Они используются для описания и анализа связности графов, а также для решения задач нахождения кратчайших путей между вершинами.

5. В теории чисел s-повы используются для изучения простых чисел и их распределения. Они позволяют определить, как часто встречаются простые числа в заданном диапазоне и оценить их распределение.

6. S-повы также применяются в теории множеств. Они используются для определения операций над множествами, таких как объединение, пересечение и разность. S-повы позволяют формально определить эти операции и исследовать свойства множеств.

Роль s-пов в геометрии

S-повы обладают свойством представлять геометрические объекты, такие как поверхности или кривые, в виде уравнений. Это позволяет упростить их описание и анализировать их свойства с помощью алгебраических методов.

Одной из важных задач, решаемых с помощью s-пов, является определение формы и размеров объекта. Например, с помощью s-пов можно определить параметры поверхности, такие как радиус кривизны или площадь. Также s-повы позволяют изучать проекции объектов, анализировать их геометрические свойства и устанавливать взаимосвязи между различными геометрическими объектами.

Применение s-пов в геометрии позволяет решать множество задач, связанных с построением, анализом и моделированием геометрических объектов. S-повы находят широкое применение в различных областях, таких как компьютерная графика, архитектура, дизайн и инженерия.

s-пов в алгебре и анализе

В анализе s-пов используются для описания процессов суперпозиции функций. Они позволяют объединить несколько функций в одну и получить новую функцию, которая является комбинацией исходных.

Пример использования s-пов в алгебре: рассмотрим функцию f(x) = x^2 и функцию g(x) = 2x + 3. Суперпозицией этих функций будет функция h(x) = (2x + 3)^2.

Пример использования s-пов в анализе: рассмотрим функцию f(x) = sin(x) и функцию g(x) = e^x. Суперпозицией этих функций будет функция h(x) = sin(e^x).

Использование s-пов в алгебре и анализе позволяет упростить задачи и получить более компактные и эффективные решения.

Преимущества использования s-пов

Применение s-пов в математике имеет ряд преимуществ, которые делают их полезными инструментами для решения различных задач.

• Гибкость: S-пов позволяют описывать сложные математические конструкции с помощью простых правил и операций над ними. Это делает их очень гибкими и удобными для использования.
• Простота использования: S-пов обладают простым и понятным синтаксисом, что делает их доступными для использования даже для начинающих математиков.
• Мощность: С помощью s-пов можно описывать и решать широкий спектр математических задач, начиная от простых арифметических операций и заканчивая высокоуровневыми алгебраическими и логическими выражениями.
• Модульность: S-пов можно комбинировать и объединять друг с другом, что позволяет строить сложные математические модели и алгоритмы из простых блоков.
• Универсальность: S-пов могут быть использованы в различных областях математики, физики, информатики и других дисциплин для моделирования, анализа и решения задач.

В целом, использование s-пов является мощным и эффективным способом работы с математическими объектами и выражениями, и позволяет упростить и ускорить процесс их анализа и решения.

Важность s-пов в математике

S-пов (или синтаксических поверхностей) играют важную роль в математике, особенно в области теории графов и комбинаторики. Они представляют собой абстрактные сетки или графы, которые используются для исследования свойств и структур математических объектов.

С помощью s-пов можно анализировать различные свойства графов и комбинаторных структур, таких как связность, циклы, пути, цветовая раскраска и многое другое. Они позволяют строить модели и формализовать проблемы, что помогает упростить их изучение и решение.

Применение s-пов в математике позволяет решать сложные задачи, связанные с комбинаторными объектами, такими как графы и сети. Они используются для анализа различных алгоритмов, оптимизации и поиска оптимальных путей в графах.

Например, с помощью s-пов можно решать задачи коммивояжера, поиска кратчайшего пути в графе или определения наименьшего остовного дерева. Они также широко используются в теории кодирования и криптографии для разработки эффективных алгоритмов шифрования и декодирования.

Важность s-пов в математике заключается в их способности представлять и анализировать сложные математические структуры и проблемы. Они помогают упростить и систематизировать исследования, позволяют находить оптимальные решения и разрабатывать эффективные алгоритмы. Без использования s-пов многие задачи в математике были бы гораздо сложнее и менее доступны для анализа и решения.

Известные математики, работающие с s-пов

С-пов (специальные поверхности) представляют собой важный инструмент в математике, используемый для изучения геометрии и топологии. С-пов активно исследуют и разрабатывают множество выдающихся математиков. Ниже приведены несколько известных математиков, работающих с s-пов:

ИмяОписание

Грегори Перельман	Российский математик, известный своей работой в области геометрии и топологии. Он доказал одну из самых известных проблем в математике — гипотезу Пуанкаре. В своих исследованиях Перельман также использовал с-пов для доказательства других важных теорем.
Уильям Тьюрстон	Американский математик, получивший Медаль Филдса за свои работы в области геометрии. Он разработал теорию Тьюрстона, которая активно использует с-пов для изучения трехмерных многообразий.
Михаил Громов	Российско-французский математик, получивший Медаль Филдса за свои работы в области геометрии. Громов внес значительный вклад в изучение с-пов и разработал концепцию гиперболических многообразий.

Это лишь некоторые известные математики, работающие с s-пов. Благодаря их исследованиям и открытиям, мы получаем более глубокое понимание геометрии и топологии, а также новые методы и подходы к решению сложных математических задач.

Вопрос-ответ:

Что такое s-пов? Как можно определить это понятие?

Понятие s-пов в математике используется для описания и изучения симметричных фигур и объектов. S-пов является кратким названием для «симметричной поверхности». Это поверхность, которая имеет особую симметрию, такую как симметрия относительно плоскости или оси. Определить s-пов можно, рассматривая его свойства симметрии и отражения.

Можно ли привести примеры s-пов?

Да, конечно! Примерами s-пов могут быть сфера, цилиндр, конус и плоскость. Сфера является примером симметричной поверхности, так как она симметрична относительно всех ее точек. Цилиндр имеет симметрию относительно его оси и плоскости основания. Конус также имеет симметрию относительно его оси и основания. А плоскость является примером симметричной поверхности, так как она симметрична относительно любой прямой, лежащей в ней.

Для чего используются s-пов в математике?

В математике s-пов используются для изучения и анализа симметричных объектов и фигур. Симметрия является важным понятием в математике и имеет широкий спектр применений. Симметричные фигуры и объекты могут быть использованы для моделирования и решения различных задач, таких как распределение сил в структурах, конструирование геометрических фигур и создание абстрактных моделей.

Какие принципы и теоремы связаны с s-пов?

Симметрия и s-пов тесно связаны с рядом принципов и теорем в математике. Например, теорема о сохранении симметрии гласит, что если математическое выражение или уравнение симметрично относительно некоторой операции, то результат этой операции также будет симметричным. Также, симметричные фигуры и объекты могут быть использованы в применении теоремы Эйлера, теоремы Пифагора и других геометрических теорем.

Что такое s-пов?

S-пов (или просто S-пов) – это обозначение для поверхностей в трехмерном пространстве, которые являются алгебраическими поверхностями четвертого порядка. Они обладают свойством симметрии и могут быть представлены уравнением вида Ax^4 + By^4 + Cz^4 + Dx^2y^2 + Ey^2z^2 + Fz^2x^2 + Gx^2 + Hy^2 + Iz^2 + J = 0, где A, B, C, D, E, F, G, H, I, J – коэффициенты, определяющие форму поверхности.

Какие примеры использования s-пов существуют в математике?

В математике s-пов широко применяются в дифференциальной геометрии, алгебре и теории вероятностей. Они являются объектом изучения при решении многих задач, связанных с алгебраическими поверхностями. Например, s-пов используются при моделировании формы биологических объектов, таких как молекулы белка, при изучении геометрических свойств поверхностей и при построении кривых четвертого порядка.

Какие особенности имеют s-пов в математике?

Одной из особенностей s-пов в математике является их симметричная форма. Это означает, что при замене переменных x, y и z местами уравнение s-пов остается неизменным. Также, s-пов образуют различные типы поверхностей, включая эллипсоиды, параболоиды, гиперболоиды и другие. Каждый тип имеет свои характеристики и свойства, которые изучаются в математике.