Относительно в математике: определение, примеры и правила использования

Относительно в математике означает, что значение или свойство зависят от других параметров или условий. Это понятие широко применяется в алгебре, геометрии и теории вероятностей. Важно учитывать относительность при решении задач и формулировании уравнений в математике.

В математике понятие относительности играет важную роль и часто используется для описания различных явлений. Относительность относится к сравнению двух или более объектов или величин и определяет, каким образом они связаны друг с другом.

В математике относительность рассматривается как отношение между двумя величинами. Оно может быть задано как числовое значение, так и словесное описание. Относительность может быть простой или сложной, и для ее определения необходимо знать значения обоих объектов, которые сравниваются.

Примеры использования относительности в математике включают в себя рассмотрение относительных величин в геометрии, таких как отношение длины к ширине или отношение площадей. Относительность также используется в экономике для оценки изменения цен на товары и услуги и в физике для определения скорости и ускорения объектов в пространстве.

Относительность и ее значение в математике

Относительность – это понятие, которое в математике используется для описания свойств объектов в сравнении с другими объектами. Относительность является основным концептом в нескольких областях математики, таких как геометрия, топология и теория относительности.

В геометрии относительность используется для описания размеров, форм и положения фигур на плоскости или в пространстве. Например, один треугольник может быть больше другого, или они могут быть подобны. В этом случае используются относительные термины, такие как «больше», «меньше», «подобно», «равносторонний» и т.д.

В топологии относительность используется для описания того, как объекты связаны друг с другом на плоскости или в пространстве. Например, две фигуры могут быть связаны топологически, если одна может быть превращена в другую без разрыва или искривления.

Теория относительности Эйнштейна также основана на понятии относительности. Для объяснения, как пространство и время взаимодействуют во Вселенной, Эйнштейн разработал теорию, которая описывает эти отношения относительно друг друга.

Использование относительности позволяет математикам изучать и описывать свойства объектов в отношении других объектов, а не только самостоятельно. Это позволяет создавать более точные и комплексные модели и теории, которые могут применяться во многих областях науки и технологий.

Эквивалентность и отношение эквивалентности

Эквивалентность – это свойство двух объектов быть равными друг другу в определенном контексте. Математически, можно сказать, что два объекта эквивалентны, если они имеют одинаковое значение по какому-то критерию. Например, два многочлена считаются эквивалентными в тех случаях, когда они имеют одинаковый набор коэффициентов.

Отношение эквивалентности – это отношение, которое устанавливается между множеством элементов на основе их эквивалентности. Математически, отношение эквивалентности является бинарным отношением на множестве, удовлетворяющим трем условиям:

• Рефлексивность: каждый элемент множества связан с самим собой;
• Симметричность: если элемент A связан с элементом B, то элемент B связан с элементом A;
• Транзитивность: если элемент A связан с элементом B, и элемент B связан с элементом C, то элемент A связан с элементом C.

Отношение эквивалентности в математике имеет широкое применение в таких областях, как алгебра, теория множеств, теория групп и др.

Например, отношение «равенства по модулю n» является отношением эквивалентности на множестве всех целых чисел. В этом случае два числа будут эквивалентны, если они дают одинаковый остаток при делении на n.

Примеры относительности и эквивалентности в математике

Относительность – это понятие, которое относит одно значение к другому в контексте сравнения. Относительность может быть выражена в процентах, коэффициентах и других математических формулах. Например, если говорят, что скорость первого автомобиля в два раза выше чем скорость второго автомобиля, то это относительность.

Эквивалентность – это понятие, когда две величины или выражения имеют равное значение. Это возможно при условии, что они являются эквивалентными по какому-то параметру. В математике, например, можно использовать эквивалентность для упрощения сложных выражений и упрощения при выполнении математических операций. Например, 1 + 1 и 2 являются эквивалентными числами, так как они имеют одинаковое значение.

Еще одним примером эквивалентности может служить правило замены. Если два выражения имеют равное значение, то мы можем заменить одно выражение на другое, сохраняя тем самым математическую эквивалентность.

Степени числа – тоже хороший пример математической эквивалентности. Например, 2*2*2 и 8 эквивалентны, так как они имеют одинаковое значение. Эквивалентность в математике основана на правилах перестановки и упрощения математических формул.

В общем, относительность и эквивалентность занимают важное место в математике и нужны для понимания многих математических концепций и операций.

Интерполяция и экстраполяция в относительных терминах

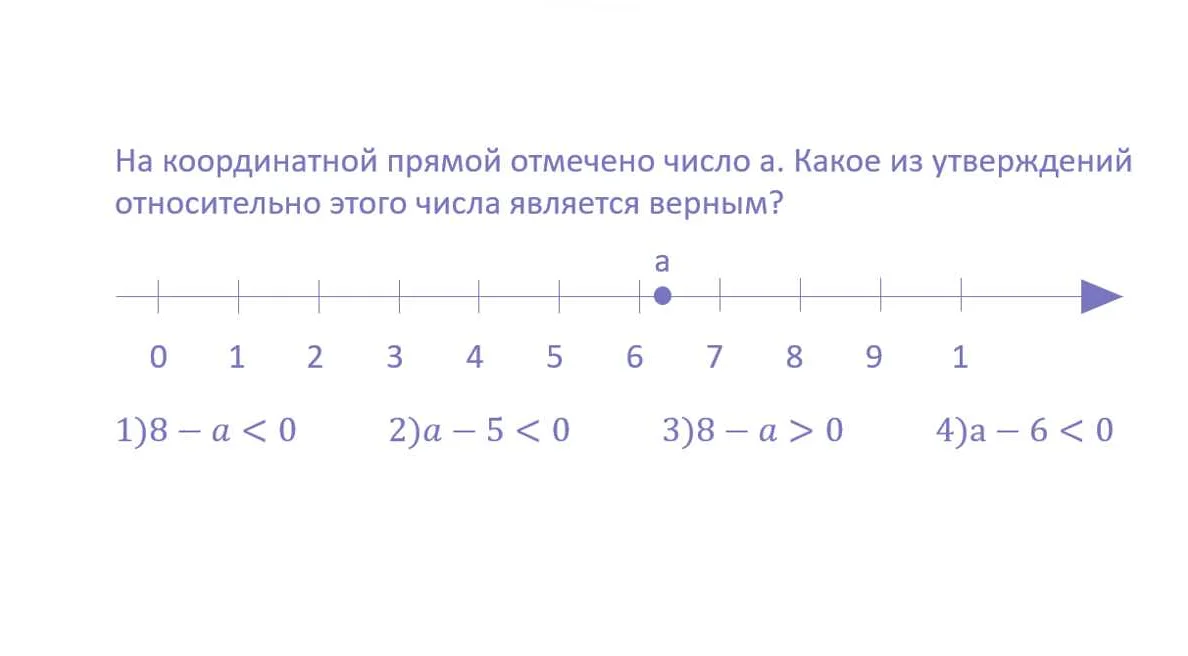
Интерполяция и экстраполяция – это математические методы, используемые для получения промежуточных значений функции или ее значения вне заданного диапазона. В относительных терминах интерполяция и экстраполяция используются для определения значения функции с учетом сопоставления ее со значениями других функций.

В задачах относительных величин, интерполяция применяется для вычисления промежуточных значений относительных величин, используя данные, полученные из других измерений. Например, для определения относительной влажности воздуха в камере с пищевыми продуктами на основе измерений температуры и давления воздуха

С другой стороны, экстраполяция используется, когда нужно получить значения функции за пределами заданных данных. Например, для прогнозирования цен на жилье на основе исторических данных о ценах на жилье в прошлом.

Следует отметить, что экстраполяция может быть менее надежной и точной, чем интерполяция, поскольку она представляет собой прогнозирование значений функции за пределами имеющихся данных и может не учитывать некоторые важные параметры, которые могут повлиять на результат.

Таким образом, интерполяция и экстраполяция являются полезными математическими методами в контексте относительных величин, и правильный выбор метода зависит от контекста и задачи, которую нужно решить.

Различные типы отношений между значениями в математике

Отношения в математике используются для описания связи между двумя или более величинами. Существует несколько типов отношений, которые могут быть встречены в математике:

1. Равенство — отношение между двумя значениями, которые имеют одинаковое значение. Обозначается символом «=».
2. Неравенство — отношение между двумя значениями, которые не имеют одинакового значения. Обозначается символами «» (больше), «=» (больше или равно).
3. Пропорциональность — отношение между двумя или более значениями, которые изменяются в соответствии с определенным правилом. Обозначается символом «∝».
4. Эквивалентность — отношение между двумя выражениями, которые имеют одинаковое значение, но могут иметь разный вид. Обозначается символом «≡».
5. Функциональное отношение — отношение между элементами двух множеств, которые связаны друг с другом таким образом, что каждому элементу первого множества соответствует ровно один элемент второго множества. Обозначается в виде «f(x) = y», где «x» — значение аргумента, «y» — значение функции.

Знание и понимание различных типов отношений между значениями в математике имеет большое значение в решении задач и построения графиков функций.

Использование относительности в функциях и алгебре

Относительность — понятие, которое широко используется в математике, в том числе в функциях и алгебре. Она определяет зависимость одного значения от другого, и как происходят изменения взаимоотношений.

В функциях, относительность играет важную роль, она позволяет определить, как изменения входных параметров влияют на выходные. Для примера, рассмотрим функцию f(x)=2x+3. Она говорит, что если мы умножим значение x на 2 и прибавим 3, мы получим соответствующее значение y. Значит, если начальное значение x изменится, то и значение функции y изменится в соответствии с формулой.

Относительность также важна в алгебре. В алгебре, отношение говорит о том, как два значения связаны друг с другом. Например, 5:10 — это отношение, которое говорит о том, что для каждых 5 единиц значение на 10 единиц больше. Таким образом, отношения помогают определить, какие изменения произойдут в значении, если мы изменим первое значение.

Относительность — это ключевое понятие в математике, которое позволяет определить зависимость между двумя значениями. Используемые в функциях и алгебре, относительные понятия могут помочь решить различные проблемы и задачи в этих областях.

Относительность и вероятность в статистике

Статистика — наука, которая изучает собранные данные, и делает выводы на основе их анализа. Для этого статистики используют понятие относительности, которое позволяет сравнивать различные данные между собой. К примеру, если нужно сравнить две группы людей, одна из которых состоит только из мужчин, а другая — только из женщин, то без понятия относительности это было бы невозможно.

Кроме того, вероятность является важным компонентом статистики, и используется чаще всего в тех случаях, когда нужно сделать прогноз на основе имеющихся данных. Например, формула вероятности может помочь предсказать результаты выборов или определить вероятность того, что какое-то событие произойдет в будущем.

Использование этих понятий в статистике требует внимательного анализа данных. Чем больше данных собрано, тем точнее будут результаты, основанные на вероятности и относительности. Именно поэтому статистика является наукой, постоянно развивающейся и улучшающейся с каждым годом.

• Выводы: Относительность и вероятность являются важными понятиями в статистике, которые позволяют сравнивать разные данные между собой, и делать прогнозы на основании этих данных.
• Анализ данных: Чем больше данных собрано, тем точнее будет результат, основанный на вероятности и относительности.
• Статистика — наука в постоянном развитии: Благодаря постоянному сбору и изучению данных, статистика продолжает развиваться и улучшаться, что в свою очередь позволяет делать более точные выводы.

Сравнение и классификация в относительных терминах

Относительные термины используются в математике для описания отношений между объектами или числами. Сравнение и классификация объектов и чисел в относительных терминах позволяет нам лучше понимать их свойства и установить иерархию.

Одним из примеров использования относительных терминов является сравнение чисел по их величине. Когда мы сравниваем два числа, мы можем сказать, что одно число больше или меньше другого. Например, мы можем сказать, что число 5 больше, чем число 2, потому что 5 находится на большей расстоянии от нуля, чем 2.

Классификация объектов в относительных терминах может помочь нам понять, как они связаны друг с другом. Например, мы можем классифицировать фрукты по их размеру: маленькие, средние и большие. Эта классификация позволит нам лучше понять, как разные фрукты связаны между собой и как они отличаются друг от друга.

Пример классификации фруктов по размеруМаленькиеСредниеБольшие

Клубника	Яблоко	Арбуз
Черешня	Груша	Дыня

В заключение, использование относительных терминов в математике позволяет нам лучше описывать и понимать отношения между объектами и числами, сравнивать их по свойствам и классифицировать в соответствии с определенными критериями.

Соотношение и пропорции в относительных терминах

В математике понятие соотношения используется для обозначения отношения одних величин к другим. Так, например, мы можем сказать, что соотношение размеров двух предметов равно 1:2. Это означает, что первый предмет в два раза меньше второго.

Одно из важнейших свойств соотношения – это его пропорциональность. Если мы имеем два соотношения, такие как 1:2 и 2:4, то они являются пропорциональными, так как они выражают одно и то же отношение двух величин.

Часто в математике мы используем пропорции для решения задач. Пропорции – это уравнения, в которых две пары соотношений равны между собой. Если мы знаем три из четырех значений в пропорции, мы можем найти четвертое значение с помощью простых математических операций.

Пример использования пропорций: если мы знаем, что 5 яблок стоят 20 рублей, то мы можем найти стоимость 8 яблок, используя пропорцию. Мы знаем, что отношение цены к количеству яблок – 20:5, и мы можем записать это соотношение в виде пропорции: 20/5 = x/8, где x – неизвестное значение. Решив эту пропорцию, мы найдем, что стоимость 8 яблок составляет 32 рубля.

Относительность и геометрия, примеры из практики

Относительность в математике проявляется во многих областях, включая геометрию. В геометрии относительность помогает определять расположение и форму фигур относительно друг друга.

Пример использования относительности в геометрии можно увидеть при решении задач на пересечение прямых и плоскостей. Например, задача может быть сформулирована так: «Два изображения фигур пересекаются на прямой. Найдите угол между этой прямой и каждой из фигур.» В данном случае, мы должны использовать относительность, чтобы определить расположение фигур относительно друг друга и угол между ними.

Относительность также может быть использована в геометрии для нахождения периметра и площади фигур. Например, в задаче «Найдите площадь треугольника, заданного тремя точками на координатной плоскости» мы должны использовать относительность, чтобы определить длины сторон треугольника и вычислить площадь.

Кроме того, относительность может быть использована в геометрии для нахождения объема фигур в трехмерном пространстве. Например, в задаче «Найдите объем параллелепипеда, заданного тремя векторами» мы должны использовать относительность, чтобы определить длины векторов и вычислить объем.

Все эти примеры демонстрируют, как относительность может быть использована в геометрии для решения различных задач. Относительность является важным концептом в математике, позволяющим нам понимать расположение и свойства фигур относительно друг друга.

Относительность и ее значение в науках о материалах и технологиях

Относительность – это понятие, которое имеет большое значение в науках о материалах и технологиях. В контексте материаловедения оно относится к свойствам материалов, которые зависят от условий их обработки и использования. Другими словами, свойства материалов относительны по отношению к процессу их получения и применения.

Например, механические свойства материалов, такие как прочность, жесткость и усталостная прочность, зависят от многих факторов, включая состояние материала, нагрузку, температуру окружающей среды и т. д. Таким образом, эти свойства относительны и могут изменяться в зависимости от контекста.

Относительность также имеет значение в технологии. Например, при производстве электроники, проводимость материалов зависит от температуры окружающей среды и внешнего электрического поля. Поэтому, чтобы обеспечить правильную работу электронных устройств, необходимо знать относительные свойства материалов и учитывать их при проектировании и производстве изделий.

Все вышесказанное подчеркивает важность понимания и учета относительности при работе с материалами и технологиями. Научные и инженерные исследования в этих областях помогают улучшить понимание относительности и использовать ее в создании более эффективных и надежных изделий и технологических процессов.

Вопрос-ответ:

Что такое относительно в математике и как это понимается?

В математике относительность означает, что значение или свойство находится в отношении с другим значением или свойством. Одно значение можно оценить только относительно другого значения. Например, если мы говорим, что одно число больше другого, то мы говорим об относительности.

Как относительность используется в алгебре?

Относительность используется в алгебре для сравнения значений и свойств. Например, если мы имеем уравнение с переменными, то мы можем использовать относительность для определения большего или меньшего значения переменной. Также, относительность используется для сравнения разных математических комбинаций.

Какие примеры использования относительности в геометрии?

В геометрии относительность используется для сравнения размеров и форм. Например, мы можем использовать относительность для определения отношения сторон в треугольнике или для определения угловых отношений в круге. Также, относительность может быть использована для сравнения двух различных геометрических фигур.

Как относительность применяется в статистике и вероятности?

В статистике и вероятности относительность используется для сравнения и анализа данных. Например, мы можем использовать относительность для определения процентного соотношения величин. Также, относительность может быть использована для сравнения полученных результатов с ожидаемыми значениями.

Какая роль относительности в физике?

В физике относительность играет важную роль в описании движения тел. Например, для описания движения объекта мы должны учитывать его скорость и направление движения относительно других объектов. Также, относительность используется для описания взаимодействия между объектами.

Как относительность используется в искусственном интеллекте?

В искусственном интеллекте относительность используется для классификации данных и обучения алгоритмов. Например, когда мы строим модель для классификации изображений, мы учитываем относительность между разными параметрами изображения, такими как цвет, тон и яркость. Это позволяет алгоритму находить более точные и точные результаты.

Какие инструменты и методы используются для работы с относительностью в математике?

Для работы с относительностью в математике используются различные методы и инструменты, такие как математические модели, системы уравнений, графики, таблицы, теория вероятности и статистики. Также, для более точной работы с относительностью, может использоваться компьютерные технологии, такие как программы для математических моделей и базы данных.

Видео по теме: