Что такое си в математике

Си в математике — это функция, которая позволяет оценить, насколько тесная связь существует между двумя переменными. Она является мерой линейной зависимости и используется для анализа статистических данных и моделирования. Узнайте, как си помогает определить, насколько сильно одна переменная влияет на другую и как она может быть использована для прогнозирования будущих значений.

Символ си (или русская буква «с») в математике используется для обозначения векторного произведения двух векторов. Он является важным понятием в векторной алгебре и находит широкое применение в различных областях науки и техники.

Определение векторного произведения можно представить следующим образом: если даны два вектора a и b, то их векторное произведение обозначается символом си и вычисляется по формуле c = a x b. Результатом векторного произведения является новый вектор, который перпендикулярен обоим исходным векторам.

Применение векторного произведения си в математике широко распространено. Оно используется в физике для решения задач, связанных с механикой твердого тела и электромагнетизмом. Также векторное произведение применяется в геометрии для определения площади треугольника и объема параллелепипеда.

Примерами использования векторного произведения си могут быть определение момента силы, вычисление магнитного поля и нахождение нормали к плоскости.

Итак, символ си в математике играет важную роль в векторных вычислениях. Он позволяет решать разнообразные задачи и находит применение в различных областях научных исследований и технологий.

Математика: Си

Си используется для решения различных математических задач, включая алгебру, теорию вероятности, физику и электротехнику. Комплексные числа могут быть использованы для представления и анализа волновых функций, электрических цепей, а также для решения уравнений и систем уравнений.

Примеры применения Си в математике:

1. Решение квадратных уравнений с комплексными корнями.
2. Изучение и моделирование колебательных процессов.
3. Анализ электрических цепей с переменными током и напряжением.
4. Исследование физических явлений, таких как электромагнетизм и оптика.

Си является важным инструментом в математике, который позволяет решать сложные задачи и анализировать различные явления и процессы.

Определение понятия «Си» в математике

Скорость света является максимальной скоростью, с которой может перемещаться информация или взаимодействовать материя. Это имеет важное значение в различных областях науки и техники, включая физику, астрономию, электронику и коммуникационные технологии.

Си также является основной константой в уравнениях электродинамики Максвелла, которые описывают взаимодействие электрических и магнитных полей. Она определяет связь между электрическими и магнитными явлениями и позволяет предсказывать поведение электромагнитных волн в различных средах и условиях.

Примеры использования «Си» в математике

Язык программирования «Си» широко используется в математике для решения различных задач. Ниже приведены некоторые примеры его применения:

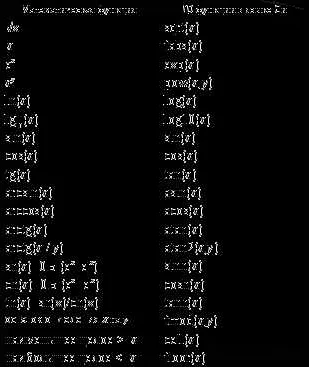
1. Вычисление функций: «Си» предоставляет возможность вычислять математические функции, такие как синус, косинус, экспонента и логарифм. Это позволяет решать сложные математические задачи с использованием стандартных или пользовательских функций.

2. Работа с матрицами: «Си» предоставляет инструменты для работы с матрицами, включая операции сложения, умножения, транспонирования и поиска определителя матрицы. Это позволяет решать задачи линейной алгебры и численных методов.

3. Решение уравнений: «Си» позволяет решать уравнения различных типов, включая линейные, квадратные и системы уравнений. Это полезно при решении задач оптимизации, моделирования процессов и анализа данных.

4. Генерация случайных чисел: «Си» предоставляет возможность генерировать случайные числа, что полезно для моделирования случайных процессов, проведения статистических экспериментов и создания случайных тестовых данных.

5. Работа с числами с плавающей точкой: «Си» поддерживает операции с числами с плавающей точкой, что позволяет решать задачи с высокой точностью, такие как вычисление интегралов, решение дифференциальных уравнений и моделирование физических процессов.

Это лишь некоторые примеры использования «Си» в математике. Благодаря своей эффективности и гибкости, «Си» является популярным выбором для реализации математических алгоритмов и приложений.

Применение «Си» в математике

Язык программирования Си широко используется в математике благодаря своей высокой производительности и мощным математическим библиотекам. Ниже приведены некоторые примеры применения Си в математических расчетах:

1. Решение уравнений и систем уравнений: Си предоставляет возможность создания программ, которые могут решать уравнения и системы уравнений. С помощью математических библиотек, таких как GNU Scientific Library (GSL), можно использовать различные методы численного решения, такие как метод Ньютона или метод простой итерации.

2. Вычисление математических функций: Си предоставляет библиотеку math.h, которая содержит множество математических функций, таких как синус, косинус, экспонента и логарифм. Эти функции могут быть использованы для вычислений в различных областях математики, включая тригонометрию, алгебру и анализ.

3. Генерация случайных чисел: Си имеет встроенную функцию rand(), которая позволяет генерировать псевдослучайные числа. Это может быть полезно для моделирования случайных процессов и проведения численных экспериментов.

4. Создание графиков и визуализация данных: Си предоставляет библиотеки, такие как GNU Plot и OpenGL, которые позволяют создавать графики и визуализировать данные. Это может быть полезно для анализа данных, построения математических моделей и визуального представления результатов математических расчетов.

Применение Си в математике не ограничивается перечисленными примерами. Благодаря своей гибкости и мощности, Си может быть использован для решения широкого спектра математических задач, начиная от простых вычислений и заканчивая сложными математическими моделями.

Как «Си» связан с другими математическими понятиями

Понятие «Си» в математике тесно связано с несколькими другими важными понятиями:

Единица измерения длины: В математике «Си» представляет собой одну из возможных единиц измерения длины. Другие единицы измерения длины, такие как метры, футы или дюймы, также широко используются в различных областях науки и техники.

Геометрия: «Си» в математике часто используется в геометрии, особенно при измерении отрезков и построении графиков. Например, «Си» может быть использована для измерения длины сторон треугольника или окружности.

Физика: В физике «Си» часто используется для измерения различных физических величин, таких как скорость, ускорение или сила. Например, «Си» может быть использована для измерения скорости движения тела или расстояния, которое оно преодолевает за единицу времени.

Инженерия: В инженерии «Си» широко используется для измерения различных параметров и характеристик, таких как длина, ширина, высота и диаметр. Например, «Си» может быть использована для измерения размеров помещения или деталей конструкции.

В целом, понятие «Си» является фундаментальным в математике и имеет широкое применение в различных областях науки и техники.

Роль «Си» в алгебре и геометрии

В геометрии Си часто используется для обозначения стороны или отрезка. Например, в треугольнике ABC, сторона AB может быть обозначена как Си. Также Си может использоваться для обозначения угла или другой величины в геометрической фигуре.

Использование Си позволяет упростить запись математических выражений и уравнений, а также облегчить работу с неизвестными значениями в алгебре и геометрии.

Пример использования Си в алгебре:

• Уравнение: 2Си + 3 = 7
• Система уравнений: Си + 2 = 5 и 3Си — 2 = 7

Пример использования Си в геометрии:

• Треугольник ABC, где Си — сторона AB
• Прямоугольник с длиной Си и шириной 5

Таким образом, Си играет важную роль в алгебре и геометрии, обозначая неизвестные значения и упрощая запись математических выражений и уравнений.

Особенности изучения «Си» в математике

Одной из основных особенностей изучения «Си» является его свойство коммутативности. Это означает, что порядок слагаемых в сумме не влияет на ее результат. Например, сумма 2 + 3 будет равна 3 + 2.

Кроме того, «Си» обладает свойством ассоциативности, что означает, что можно менять порядок скобок при сложении нескольких чисел. Например, сумма (2 + 3) + 4 будет равна 2 + (3 + 4).

Изучение «Си» также позволяет осуществлять сложение чисел в различных системах счисления. Например, в двоичной системе счисления, где используются только две цифры 0 и 1, сумма двух чисел может быть получена путем сложения соответствующих цифр каждого разряда.

Применение «Си» в математике широко распространено. Оно используется для решения различных задач, включая нахождение суммы ряда чисел, вычисление площадей и объемов, нахождение среднего значения и т.д.

В заключение, изучение «Си» в математике позволяет развить навыки сложения и понимание основных принципов математических операций. Это является неотъемлемой частью математического образования и используется во многих областях науки и техники.

Вопрос-ответ:

Что такое си в математике?

Си в математике обозначает синус, одну из тригонометрических функций. Это отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.

Как определить значение синуса?

Значение синуса можно определить с помощью таблицы значений или с помощью калькулятора, вводя угол в радианах или градусах.

Какие свойства имеет синус в математике?

Синус обладает несколькими свойствами: периодичностью, четностью, ограниченностью и монотонностью. Он также является непрерывной функцией.

Какой пример применения синуса в математике?

Примером применения синуса в математике может быть решение треугольников, нахождение высоты, определение углов и длин сторон треугольника.

Какие есть формулы, связанные с синусом?

К некоторым формулам, связанным с синусом, относятся формула сложения синусов, формула удвоения синуса, формула половинного угла и тригонометрический треугольник.

Значение «Си» для решения математических задач

В математике понятие «Си» обозначает сумму элементов в последовательности чисел. Этот термин происходит от латинского слова «summa», что означает «сумма». В контексте математических задач «Си» представляет собой сумму всех чисел в заданной последовательности.

Для примера, рассмотрим последовательность чисел от 1 до 5. Сумма этих чисел будет равна «Си» и записывается следующим образом: Си = 1 + 2 + 3 + 4 + 5. В данном случае, «Си» будет равно 15.

Понятие «Си» имеет широкое применение в математике и используется для решения различных задач. Одним из примеров применения «Си» является вычисление среднего арифметического значения последовательности чисел. Для этого необходимо найти сумму всех чисел в последовательности и поделить ее на количество чисел в последовательности.

Также «Си» может быть использовано для нахождения общего числа элементов в последовательности, если известны первый и последний элементы, а также шаг между ними. Для этого необходимо использовать формулу: Си = (последний элемент — первый элемент + шаг) / шаг.

Таким образом, понятие «Си» является важным и полезным инструментом при решении математических задач. Оно позволяет нам вычислять сумму чисел в последовательности, находить среднее арифметическое и определять общее количество элементов в последовательности.

Видео по теме: