Что такое корреляция в математике

Корреляция – это статистическая мера, которая показывает, насколько две или более переменные связаны между собой. В математике, корреляция измеряет степень зависимости между величинами и может быть положительной, отрицательной или отсутствовать. Узнайте, как корреляция используется для анализа данных и прогнозирования будущих значений.

Корреляция — это статистическая мера, которая описывает взаимосвязь между двумя переменными. В математике корреляция позволяет определить, насколько сильно и в каком направлении две переменные меняются вместе. Она может быть положительной, если две переменные движутся в одном направлении, отрицательной, если они движутся в противоположных направлениях, или отсутствовать, если две переменные никак не связаны между собой.

Основными понятиями, связанными с корреляцией, являются коэффициент корреляции и показатель значимости. Коэффициент корреляции измеряет силу и направление связи между переменными и может принимать значения от -1 до 1. Значение -1 означает полную отрицательную корреляцию, 1 — полную положительную корреляцию, а 0 — отсутствие корреляции. Показатель значимости позволяет определить, насколько надежны результаты и насколько вероятно, что значение коэффициента корреляции является истинным, а не случайным.

Корреляция используется во многих областях, таких как экономика, психология, социология и другие, для изучения и предсказания взаимосвязей между различными переменными. Например, в экономике корреляция может помочь определить, насколько сильно изменение одной переменной, например, цены на нефть, может влиять на изменение другой переменной, например, инфляции. В психологии корреляция может помочь выявить связь между уровнем стресса и заболеваемостью, а в социологии — между уровнем образования и уровнем дохода.

Понимание корреляции в математике является важным инструментом для анализа данных и принятия решений. Оно позволяет нам определить, насколько две переменные связаны между собой и какая связь может существовать между ними в будущем. Знание основных понятий и принципов корреляции помогает нам лучше понять и объяснить мир вокруг нас и сделать более точные прогнозы о будущих событиях и тенденциях.

Основные понятия и принципы корреляции в математике

Основными понятиями, используемыми при изучении корреляции, являются корреляционный коэффициент и диапазон значений. Корреляционный коэффициент — это числовая мера, которая показывает силу и направление взаимосвязи между переменными. Он может принимать значения от -1 до 1, где -1 означает полную обратную взаимосвязь, 1 — полную прямую взаимосвязь, и 0 — отсутствие взаимосвязи.

Диапазон значений корреляционного коэффициента зависит от используемого метода расчета, но наиболее распространенными являются коэффициент Пирсона и коэффициент Спирмена. Коэффициент Пирсона используется для измерения линейной взаимосвязи, а коэффициент Спирмена — для измерения монотонной взаимосвязи.

При проведении анализа корреляции важно учитывать, что корреляция не всегда означает причинно-следственную связь между переменными. Она лишь показывает наличие или отсутствие связи между ними. Поэтому важно проводить дополнительные исследования, чтобы подтвердить или опровергнуть причинно-следственную связь.

Видео по теме:

Что такое корреляция в математике и зачем она нужна?

Основная цель изучения корреляции в математике – выявить и описать связи между различными явлениями или явлениями и их характеристиками. Понимание этих связей может служить основой для прогнозирования и анализа данных, что делает корреляцию полезным инструментом в научных исследованиях, экономике, социологии, биологии и других областях.

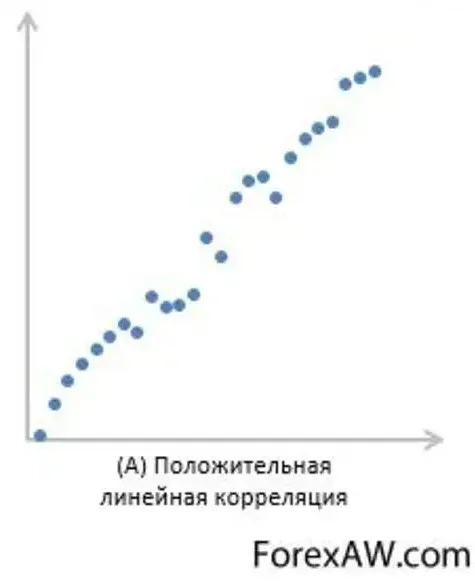
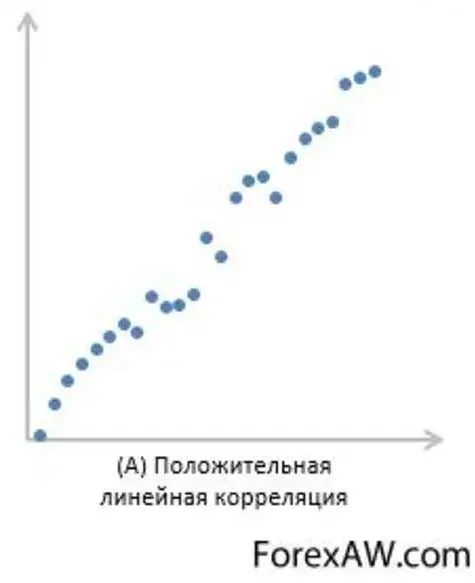
Корреляция может быть положительной, если две величины изменяются в одном направлении (т.е. при увеличении одной величины, другая также увеличивается), или негативной (инверсионной), если две величины изменяются в разных направлениях (т.е. при увеличении одной величины, другая уменьшается).

Однако важно понимать, что корреляция не означает причинно-следственную связь между переменными. Она лишь указывает на наличие связи и позволяет делать выводы о возможных взаимосвязях между ними.

Виды корреляции и их особенности

1. Положительная корреляция

Положительная корреляция характеризуется тем, что значения двух переменных изменяются в одном направлении: при увеличении одной переменной увеличивается и вторая, а при уменьшении одной переменной уменьшается и вторая. Коэффициент корреляции в положительной корреляции находится в пределах от 0 до 1.

2. Отрицательная корреляция

Отрицательная корреляция возникает, когда значения двух переменных изменяются в разных направлениях: при увеличении одной переменной уменьшается вторая, а при уменьшении одной переменной увеличивается вторая. Коэффициент корреляции в отрицательной корреляции находится в пределах от -1 до 0.

3. Нейтральная корреляция

Нейтральная (нулевая) корреляция предполагает отсутствие взаимосвязи между двумя переменными. При данной корреляции коэффициент корреляции равен 0.

4. Статистическая и практическая значимость

Статистическая значимость корреляции позволяет определить, насколько вероятно наличие взаимосвязи между переменными. Практическая значимость корреляции определяет, насколько эта взаимосвязь может быть полезной или применимой в практическом смысле.

5. Линейная и нелинейная корреляция

Линейная корреляция предполагает, что связь между переменными может быть описана линейной функцией. Нелинейная корреляция возникает, когда связь между переменными не может быть описана линейной функцией и имеет иные, более сложные формы функциональной зависимости.

6. Сильная и слабая корреляция

Сильная корреляция означает, что значения переменных тесно связаны друг с другом и изменяются в сходном направлении. Слабая корреляция говорит о менее выраженной связи между переменными.

7. Парная и множественная корреляция

Парная корреляция изучает взаимосвязь между двумя переменными. Множественная корреляция анализирует зависимость между одной зависимой переменной и несколькими независимыми переменными.

8. Передача причинности

Корреляция не гарантирует наличие причинно-следственной связи между переменными. Она лишь показывает степень взаимосвязи между ними, но не указывает на причинность.

9. Критический анализ

Для корректного использования и интерпретации корреляции необходим критический анализ данных, учет контекста и исключение возможных влияний других переменных.

Вопрос-ответ:

Что такое корреляция в математике?

Корреляция в математике — это статистическая зависимость между двумя или более переменными. Она показывает, насколько сильно и с каким направлением две переменные связаны между собой.

Как измеряется корреляция?

Корреляция измеряется с помощью коэффициента корреляции, который может принимать значения от -1 до +1. Значение +1 означает положительную корреляцию, -1 — отрицательную корреляцию, а значение 0 — отсутствие корреляции.

Какой коэффициент корреляции говорит о сильной зависимости между переменными?

Коэффициент корреляции близкий к +1 или -1 говорит о сильной зависимости между переменными. Например, если коэффициент равен 0.8, это означает, что переменные сильно положительно связаны.

Какие принципы лежат в основе корреляции?

Основными принципами корреляции являются: независимость переменных, линейность связи, отсутствие выбросов и случайной ошибки в данных. Если эти принципы нарушены, то корреляция может быть неправильно интерпретирована.

Какая разница между корреляцией и причинно-следственной связью?

Корреляция показывает только статистическую связь между переменными, а причинно-следственная связь говорит о том, что изменение одной переменной вызывает изменение другой. Корреляция не гарантирует наличие причинно-следственной связи, а только указывает на наличие или отсутствие статистической зависимости.

Как определить корреляцию между двумя переменными?

Для определения корреляции между двумя переменными нужно взять выборку данных и рассчитать коэффициент корреляции. Самый распространенный коэффициент корреляции — это коэффициент Пирсона, который измеряет линейную зависимость между переменными и принимает значения от -1 до 1. Значение близкое к 1 указывает на положительную линейную зависимость, близкое к -1 — на отрицательную, а значение близкое к 0 — на отсутствие линейной зависимости.

Как интерпретировать значение коэффициента корреляции?

Значение коэффициента корреляции позволяет сделать выводы о силе и направлении линейной зависимости между переменными. Если коэффициент корреляции близок к 1, это указывает на сильную положительную линейную зависимость, то есть чем больше одна переменная, тем больше другая. Если коэффициент близок к -1, это указывает на сильную отрицательную линейную зависимость, то есть чем больше одна переменная, тем меньше другая. Если коэффициент близок к 0, это указывает на отсутствие линейной зависимости между переменными.

Как измеряется степень корреляции?

Коэффициент Пирсона (обозначается как r) измеряет линейную связь между переменными. Он принимает значения от -1 до 1, где 1 указывает на положительную линейную связь, -1 указывает на отрицательную линейную связь, а 0 указывает на отсутствие линейной связи.

Коэффициент Спирмена (обозначается как ρ) измеряет монотонную связь между переменными, то есть связь, которая не обязательно является линейной. Он также принимает значения от -1 до 1, с тем же смыслом, что и коэффициент Пирсона.

Оба коэффициента корреляции могут быть вычислены с использованием статистического программного обеспечения или специальных калькуляторов. После вычисления коэффициента корреляции, можно проанализировать его значение, чтобы сделать выводы о степени связи между переменными. Чем ближе значение коэффициента к 1 или -1, тем сильнее связь между переменными.

Корреляция и причинно-следственные связи

Однако важно отметить, что корреляция не является доказательством причинно-следственной связи между переменными. Простыми словами, высокая корреляция между двумя переменными не означает, что одна переменная вызывает изменения в другой переменной.

Например, если исследование показывает высокую корреляцию между уровнем образования и заработной платой, это не означает, что образование напрямую влияет на заработную плату. Возможно, существует третий фактор, такой как опыт работы, который одновременно влияет на оба этих показателя.

Поэтому для выявления причинно-следственной связи между переменными требуется проведение дополнительного исследования и учет других факторов, которые могут влиять на изменение переменных.

Тем не менее, корреляция является важным инструментом для изучения взаимосвязей между переменными и может помочь в определении степени влияния одной переменной на другую. Она позволяет установить наличие или отсутствие связи между переменными и оценить ее силу.

Важно помнить, что корреляция не гарантирует наличие причинно-следственной связи и требует дополнительного исследования для подтверждения результатов.

Значение корреляции в научных исследованиях

Значение корреляции заключается в том, что она позволяет установить, насколько сильно две переменные связаны друг с другом. Корреляция может быть положительной, когда увеличение значения одной переменной сопровождается увеличением значения другой переменной, или отрицательной, когда увеличение значения одной переменной сопровождается уменьшением значения другой переменной.

Корреляция имеет важное значение для научных исследований, так как она позволяет выявить закономерности и тенденции в данных. Например, исследователь может использовать корреляцию для определения связи между потреблением кофе и риском развития определенного заболевания. Если корреляция будет выявлена, это может указывать на то, что потребление кофе может быть фактором, влияющим на риск заболевания.

Кроме того, корреляция может использоваться для предсказания значений одной переменной на основе значений другой переменной. Например, исследователь может использовать корреляцию между количеством часов подготовки и результатами теста, чтобы предсказать ожидаемый результат теста для студента, затратившего определенное количество времени на подготовку.

Однако важно понимать, что корреляция не всегда означает причинно-следственную связь между переменными. Выявление корреляции между двумя переменными не означает, что одна переменная является причиной изменений в другой переменной. Для определения причинно-следственной связи между переменными необходимы дополнительные исследования и проверка гипотез.

Значение корреляцииСтепень связи

0	Отсутствие связи
0.1-0.3	Слабая связь
0.3-0.5	Умеренная связь
0.5-0.7	Заметная связь
0.7-0.9	Высокая связь
0.9-1	Очень высокая связь

Как интерпретировать результаты корреляционного анализа?

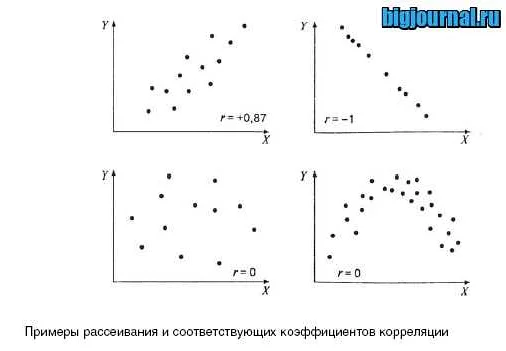
После проведения корреляционного анализа важно правильно интерпретировать полученные результаты. В основном, результаты корреляционного анализа выражаются в коэффициенте корреляции, который находится в диапазоне от -1 до 1.

Если коэффициент корреляции близок к 1, то это означает, что между двумя переменными существует сильная прямая связь. То есть, при увеличении значения одной переменной, значения другой переменной также увеличиваются. Например, если коэффициент корреляции между уровнем образования и заработной платой равен 0,8, это означает, что люди с высоким уровнем образования имеют более высокую заработную плату.

Если коэффициент корреляции близок к -1, то это означает, что между двумя переменными существует сильная обратная связь. То есть, при увеличении значения одной переменной, значения другой переменной уменьшаются. Например, если коэффициент корреляции между количеством часов, проведенных на учебе, и количеством пропущенных занятий равен -0,9, это означает, что студенты, которые тратят больше времени на учебу, пропускают меньше занятий.

Если коэффициент корреляции близок к нулю, то это означает, что между двумя переменными нет существенной связи. То есть, изменение значений одной переменной не влияет на значения другой переменной. Например, если коэффициент корреляции между ростом человека и его любимым цветом равен 0,1, это означает, что рост человека не имеет никакого влияния на его предпочтение в выборе любимого цвета.

Важно помнить, что корреляция не всегда означает причинно-следственную связь между переменными. Корреляция лишь показывает степень связи между переменными, но не указывает на то, какая переменная вызывает изменение в другой переменной.

Ограничения и проблемы корреляционного анализа

Во-первых, корреляция не означает причинно-следственную связь между переменными. То есть, если две переменные коррелируют между собой, это не означает, что одна переменная является причиной изменения другой переменной. Корреляция лишь указывает на существование связи между переменными, но не позволяет определить, какая переменная является причиной, а какая следствием.

Во-вторых, корреляционный анализ предполагает линейную связь между переменными. Если связь между переменными является нелинейной, корреляция может не отражать эту связь или давать неверные результаты. В таких случаях может потребоваться использование других методов анализа, например, регрессионного анализа.

Также, корреляционный анализ предполагает наличие стабильной связи между переменными во времени или в пространстве. Если связь между переменными меняется со временем или в разных ситуациях, корреляция может быть непостоянной. Поэтому важно учитывать контекст и особенности исследования при интерпретации результатов корреляционного анализа.

Одной из проблем корреляционного анализа является наличие выбросов или необычных наблюдений в данных. Такие выбросы могут исказить результаты корреляционного анализа, особенно если они являются единичными случаями. Поэтому перед проведением корреляционного анализа рекомендуется проверить данные на наличие выбросов и, если необходимо, исключить их из анализа.

Наконец, корреляционный анализ может привести к ложным или неправильным выводам, если не учитывать другие факторы, которые могут влиять на результаты. Например, корреляция между двумя переменными может быть обусловлена третьей переменной, которая не была учтена в анализе. Поэтому важно проводить более глубокий анализ и контролировать влияние других факторов на результаты корреляционного анализа.

Ограничения и проблемы корреляционного анализа

1. Корреляция не означает причинно-следственную связь между переменными

2. Корреляционный анализ предполагает линейную связь между переменными

3. Корреляционный анализ предполагает стабильную связь между переменными во времени или в пространстве

4. Наличие выбросов или необычных наблюдений в данных может исказить результаты корреляционного анализа

5. Неучтенные факторы могут привести к ложным или неправильным выводам в корреляционном анализе

Примеры применения корреляционного анализа в реальной жизни

1. Медицина: Корреляционный анализ позволяет исследовать взаимосвязь между различными факторами здоровья и заболеваниями. Например, исследования могут показать, что уровень физической активности коррелирует с риском сердечно-сосудистых заболеваний.

2. Экономика: Корреляционный анализ может помочь выявить связь между экономическими переменными. Например, исследования могут показать, что рост ВВП коррелирует с уровнем безработицы или инфляции.

3. Психология: Корреляционный анализ используется для изучения связи между различными психологическими переменными. Например, исследования могут показать, что уровень стресса коррелирует с уровнем депрессии или счастья.

4. Образование: Корреляционный анализ может помочь выявить взаимосвязь между различными факторами образования. Например, исследования могут показать, что уровень образования коррелирует с доходом или успехом на рабочем месте.

5. Маркетинг: Корреляционный анализ используется для изучения связи между различными маркетинговыми переменными. Например, исследования могут показать, что уровень рекламного бюджета коррелирует с объемом продаж или уровнем узнаваемости бренда.

Это лишь некоторые примеры применения корреляционного анализа в реальной жизни. Он может использоваться во множестве других областей для выявления взаимосвязей и понимания сложных систем и явлений.