Что такое симметрия в математике кратко

Симметрия в математике — это свойство фигур или объектов, которые могут быть разделены на две половины, которые симметричны относительно некоторой оси или плоскости. Знание симметрии помогает математикам и физикам решать различные задачи и анализировать формы и структуры в природе и искусстве.

Симметрия – это одно из основных понятий в математике, которое является важным инструментом для понимания и описания многих явлений и объектов. Она описывает отношение между двумя объектами, которые симметричны друг относительно друга. В математике симметрия используется для анализа геометрических фигур, функций, уравнений и других математических объектов.

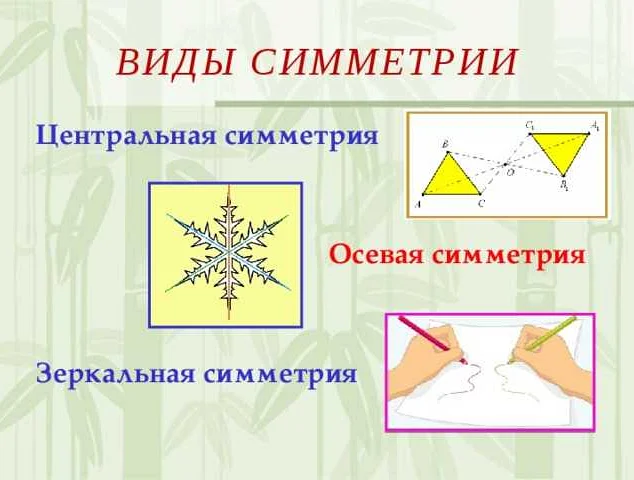
Симметрия может быть различных видов, включая осевую симметрию, центральную симметрию и другие. Осевая симметрия означает, что объект остается неизменным при повороте на определенный угол вокруг оси симметрии. Центральная симметрия означает, что объект остается неизменным при отражении относительно точки, называемой центром симметрии.

Симметрия имеет множество применений в различных областях, включая физику, химию, биологию и искусство. В физике симметрия играет важную роль в понимании законов природы и в разработке моделей. В химии симметрия используется для описания молекулярной структуры веществ. В биологии симметрия помогает понять анатомию организмов и их эволюцию. В искусстве симметрия используется для создания эстетических и гармоничных композиций.

Симметрия в математике: краткое объяснение

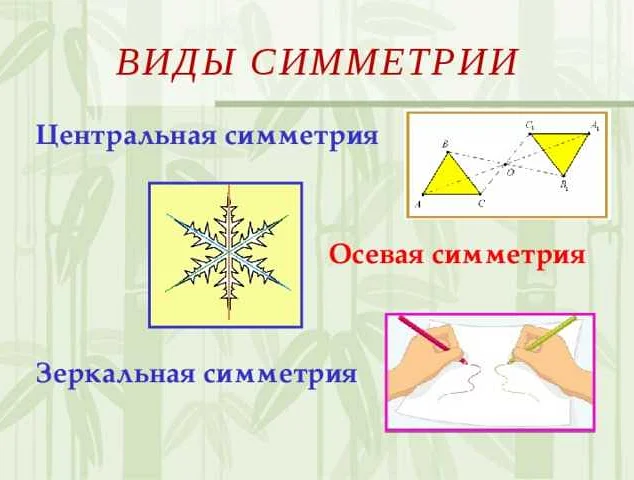
Симметрия может быть разделена на несколько видов:

• Осевая симметрия — это тип симметрии, при котором фигура или объект совпадает с самим собой относительно оси. Например, круг является осевой симметричной фигурой, так как любая прямая линия, проходящая через его центр, разделяет его на две одинаковые части.
• Плоская симметрия — это тип симметрии, при котором фигура или объект совпадает с самим собой относительно плоскости. Например, квадрат является плоской симметричной фигурой, так как его можно повернуть на 180 градусов относительно горизонтальной или вертикальной оси и получить ту же самую фигуру.
• Центральная симметрия — это тип симметрии, при котором фигура или объект совпадает с самим собой относительно центральной точки. Например, крест является центрально симметричной фигурой, так как любая прямая линия, проходящая через его центр, разделяет его на две одинаковые половины.

Симметрия имеет множество применений в математике и других науках. Она помогает анализировать и классифицировать объекты, понимать их свойства и взаимосвязи. Изучение симметрии позволяет развивать логическое мышление, абстрактное и геометрическое мышление, а также способности к анализу и решению проблем.

Симметрия: определение и основные принципы

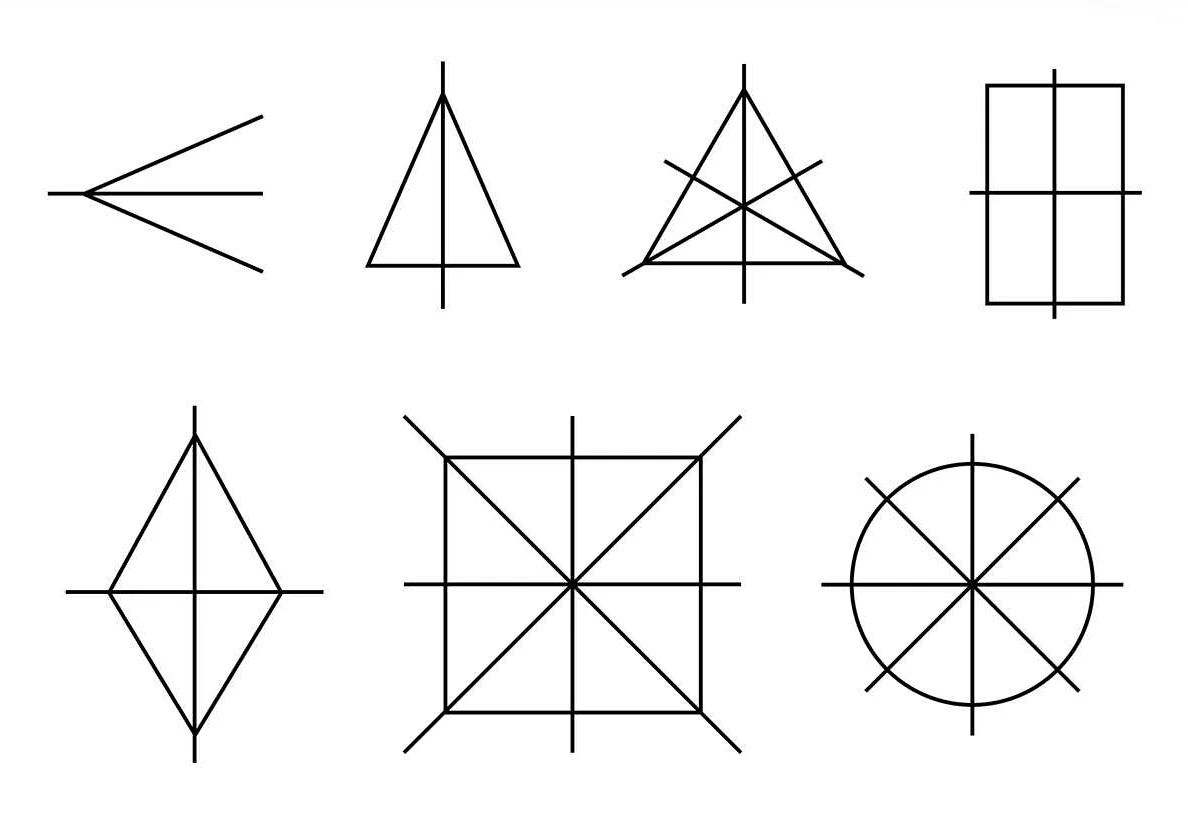
Основными принципами симметрии являются:

1. Осевая симметрия — это тип симметрии, для которой существует ось, вокруг которой объект отображается на самого себя. На практике это означает, что объект имеет две половины, которые являются зеркальными отражениями друг друга.
2. Поворотная симметрия — это тип симметрии, при которой объект отображается на себя после поворота на определенный угол. Объект может иметь несколько осей поворотной симметрии, вокруг которых он отображается на самого себя.
3. Трансляционная симметрия — это тип симметрии, при которой объект отображается на себя после сдвига на определенное расстояние. Такой тип симметрии часто наблюдается в регулярных структурах, таких как решетки или мозаики.

Симметрия широко применяется в различных областях, таких как геометрия, физика, химия и дизайн. Она помогает нам понять и описать закономерности и упорядоченность в окружающем нас мире. Изучение симметрии позволяет нам увидеть гармонию и красоту в разнообразии форм и структур.

Типы симметрии в математике

1. Осевая симметрия: Осевая симметрия означает, что фигура может быть разделена на две одинаковые половины относительно оси симметрии. Осевая симметрия также называется симметрией относительно прямой.

2. Центральная симметрия: Центральная симметрия означает, что фигура выглядит одинаково относительно центра. Центральная симметрия также называется симметрией относительно точки.

3. Поворотная симметрия: Поворотная симметрия означает, что фигура может быть повернута на определенный угол и останется неизменной. Вращение на угол 180 градусов является наиболее распространенным видом поворотной симметрии.

4. Пятикратная симметрия: Пятикратная симметрия означает, что фигура может быть повернута на угол 72 градуса и останется неизменной. Этот тип симметрии встречается у пятиугольника.

5. Фризовая симметрия: Фризовая симметрия означает, что фигура может быть повторена вдоль прямой и останется неизменной. Фризовая симметрия часто встречается в традиционных узорах и орнаментах.

6. Сферическая симметрия: Сферическая симметрия означает, что фигура выглядит одинаково при вращении вокруг оси, проходящей через ее центр. Этот тип симметрии типичен для шара или сферы.

Понимание различных типов симметрии помогает ученым и математикам анализировать и классифицировать фигуры, а также разрабатывать новые концепции в различных областях математики.

Симметрия в геометрии

Симметрия относительно оси — это тип симметрии, при котором фигура зеркально отражается относительно некоторой линии, называемой осью симметрии. Обычно ось симметрии является прямой линией, проходящей через центр фигуры. Например, круг является фигурой с бесконечным количеством осей симметрии, так как он может быть отражен относительно любой прямой, проходящей через его центр.

Симметрия относительно точки — это тип симметрии, при котором фигура зеркально отражается относительно некоторой точки, называемой центром симметрии. Центр симметрии является точкой, вокруг которой фигура сохраняет свою форму при отражении. Например, равносторонний треугольник имеет центр симметрии, который совпадает с его центром.

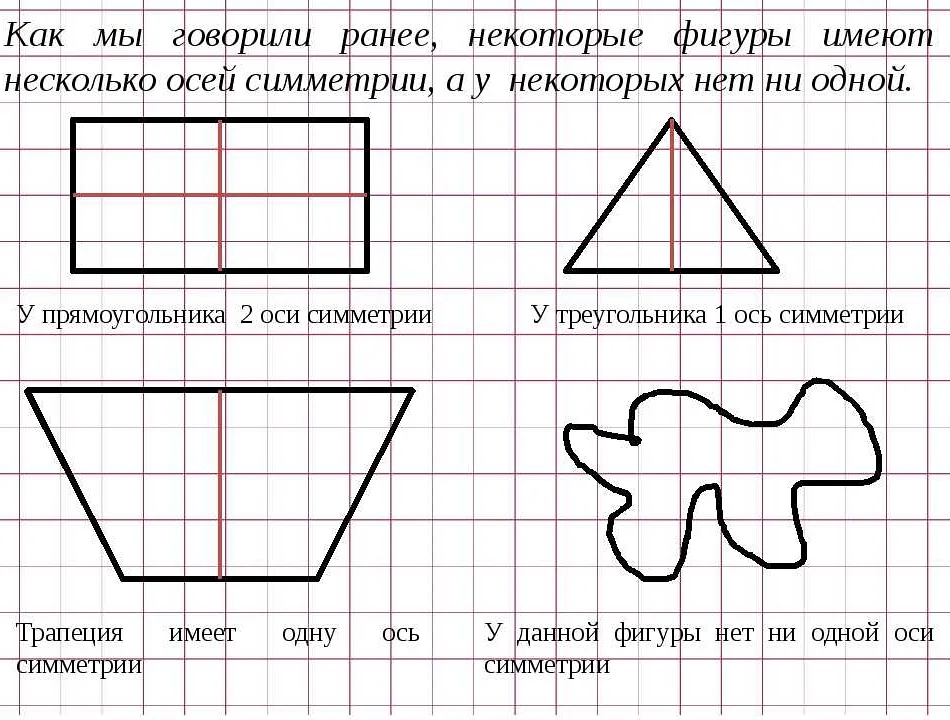
Симметрия относительно плоскости — это тип симметрии, при котором фигура зеркально отражается относительно некоторой плоскости. Плоскость симметрии является плоскостью, которая разделяет фигуру на две зеркально симметричные части. Например, прямоугольник имеет одну плоскость симметрии, которая перпендикулярна его длинной стороне и делит его на две равные половины.

Симметрия в геометрии имеет множество применений и используется для анализа и классификации различных фигур. Она также играет важную роль в создании и изучении геометрических моделей в науке и технике.

Симметрия в алгебре

Один из примеров симметрии в алгебре – это симметрия функции. Функция называется симметричной, если значения функции на одинаковом расстоянии от оси симметрии равны. Например, функция f(x) = x^2 является симметричной относительно оси y, так как f(x) = f(-x).

Симметрия также может применяться к уравнениям и графам. Например, уравнение x^2 + y^2 = 1 описывает окружность, которая является симметричной относительно осей координат. График уравнения имеет симметрию относительно осей координат и центра окружности.

Симметрия в алгебре играет важную роль в решении уравнений и нахождении симметричных формул. Она позволяет упростить выражения и найти общие закономерности.

ПримерФормулаСимметрия

Квадрат	a^2	a^2 = a · a
Куб	a^3	a^3 = a · a · a

Таким образом, симметрия в алгебре помогает упростить и анализировать алгебраические объекты и выражения, позволяя найти закономерности и общие свойства.

Применение симметрии в решении задач

Симметрия играет важную роль в математике и находит применение в решении различных задач. Она помогает упростить задачу, найти решение или выявить особенности объектов.

Одним из способов использования симметрии является поиск симметричных свойств объектов. Например, если мы знаем, что фигура имеет ось симметрии, то мы можем использовать это свойство для нахождения другой части фигуры, зная только ее часть. Это может быть полезно при решении геометрических задач, таких как нахождение площади или периметра фигуры.

Симметрия также может использоваться для упрощения вычислений. Например, при решении уравнений или систем уравнений, если у нас есть симметричные корни или симметричные уравнения, мы можем использовать свойства симметрии для сокращения вычислений и нахождения решения.

Кроме того, симметричные объекты могут иметь особенности, которые можно использовать для решения задач. Например, симметрия может помочь определить, какие точки находятся на одинаковом расстоянии от центра симметрии, или какие точки являются симметричными относительно определенной оси.

Использование симметрии в решении задач позволяет нам более эффективно и точно анализировать и находить решения. Это одна из важных концепций в математике, которая находит широкое применение в различных областях.

Видео по теме:

Вопрос-ответ:

Как можно объяснить понятие симметрии в математике?

Симметрия в математике — это свойство фигур, в которых можно найти ось, относительно которой части фигуры совпадают друг с другом. В результате симметрии фигуры обладают гармоничным и сбалансированным внешним видом.

Какие виды симметрии существуют в математике?

В математике существуют различные виды симметрии: осевая симметрия, центральная симметрия и поворотная симметрия. Осевая симметрия — это симметрия относительно прямой оси, центральная симметрия — это симметрия относительно точки, а поворотная симметрия — это симметрия относительно поворота на определенный угол.

Какие примеры симметрии можно найти в повседневной жизни?

Примеры симметрии можно найти во многих объектах повседневной жизни. Например, многие лица людей имеют осевую симметрию — половины лица симметричны относительно носа. Также многие предметы декора, такие как картины, имеют симметричные элементы, что делает их более привлекательными для глаза.

Зачем изучать симметрию в математике?

Изучение симметрии в математике имеет несколько целей. Во-первых, это помогает понять принципы гармонии и баланса в природе и искусстве. Во-вторых, симметрия играет важную роль в различных областях науки, таких как кристаллография и физика. Наконец, изучение симметрии развивает логическое мышление и способствует развитию воображения.

Симметрия в природе и искусстве

В природе мы можем обнаружить множество примеров симметрии. Например, многие цветы имеют симметричную структуру. Один из наиболее известных примеров — это мак, у которого лепестки расположены вокруг центральной оси симметрии. Другой пример — снежинки, которые имеют симметричные формы и узоры.

Симметрия также играет важную роль в искусстве. Множество произведений искусства, таких как картины, скульптуры и архитектурные сооружения, используют симметрию для создания гармонии и эстетического воздействия. Например, симметричная композиция может создать ощущение равновесия и покоя, в то время как асимметричная композиция может вызывать интерес и движение.

Цветы с симметричной структурой	Снежинки с симметричными формами и узорами	Картина с использованием симметрии

Симметрия в природе и искусстве подчеркивает гармонию и красоту, которые присутствуют вокруг нас. Она позволяет нам лучше понять мир и наслаждаться его прекрасными проявлениями.

Эволюция понятия симметрии в истории математики

В Древнем Египте симметрия была широко использована в архитектуре и искусстве. Основным принципом была горизонтальная симметрия, при которой объект или рисунок мог быть разделен на две равные части, зеркально отражающие друг друга.

Греки, особенно Платон и Евклид, внесли значительный вклад в понимание симметрии. Они разработали систему геометрии, которая включала в себя понятие симметрии. Платон в своих работах утверждал, что симметрия имеет глубокий философский смысл и отражает гармонию и идеальность мира.

В Средние века понятие симметрии оставалось в значительной степени неизменным. Основной интерес был связан с симметрией в искусстве и архитектуре, особенно в соборах и дворцах. Развитие математики в этот период было ограничено, и идеи симметрии не получили новых открытий или интерпретаций.

Однако с появлением современной математики в XVII и XVIII веках понятие симметрии стало играть все более важную роль. Математики, такие как Лобачевский и Риман, начали изучать неевклидову геометрию, которая предполагала наличие других видов симметрии, в том числе гиперболической и эллиптической симметрии.

В XX веке симметрия стала ключевым понятием в абстрактной алгебре и физике. Математики и физики изучали группы симметрии и применяли их для описания фундаментальных законов природы. Понятие симметрии получило новую интерпретацию и стало одним из основных инструментов в современной математике и физике.