Симметрия что это в математике
Содержимое
- 1 Симметрия что это в математике
- 1.1 Что такое симметрия в математике?
- 1.2 Определение и основные понятия
- 1.3 Виды симметрии в математике
- 1.4 Симметрия по отношению к прямой
- 1.5 Симметрия по отношению к точке
- 1.6 Симметрия по отношению к плоскости
- 1.7 Примеры симметрии в математике
- 1.8 Значение симметрии в различных областях
- 1.9 Вопрос-ответ:
- 1.9.0.1 Что такое симметрия в математике?
- 1.9.0.2 Какие бывают виды симметрии в математике?
- 1.9.0.3 Какие примеры симметрии можно привести?
- 1.9.0.4 Какая роль симметрии в математике?
- 1.9.0.5 Каким образом симметрия применяется в реальной жизни?
- 1.9.0.6 Что такое симметрия в математике?
- 1.9.0.7 Какие бывают виды симметрии в математике?
- 1.10 Видео по теме:
Симметрия — это важное понятие в математике, которое описывает равенство частей объекта относительно определенной оси или плоскости. В данной статье мы разберем основные виды симметрии и их применение в различных областях математики.
Симметрия — одно из важнейших понятий в математике, которое широко используется в различных областях этой науки. Она является основой для понимания многих математических концепций и имеет много приложений в реальном мире. Симметрия говорит о том, что некоторый объект или система имеют одинаковые или соответствующие части в отношении определенной операции или преобразования.
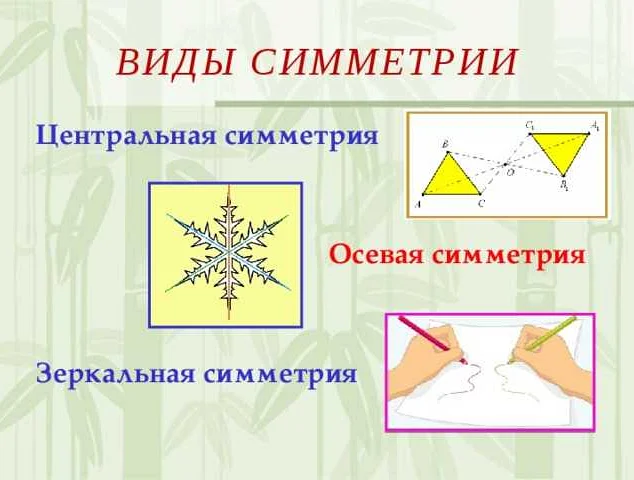
Симметрия может быть представлена в различных формах и виде. Одним из самых распространенных видов симметрии является осевая симметрия, когда объект или фигура имеют ось, вдоль которой они симметричны. Второй вид — центральная симметрия, где объект или фигура имеют точку, называемую центром симметрии, относительно которой они симметричны.
Примером осевой симметрии может служить изображение бабочки. Если провести линию через ее тело, то левая и правая половины будут зеркальными отражениями друг друга. В то же время, примером центральной симметрии может служить изображение снежинки. Если провести линии от ее центра ко всем шести концам, каждая из них будет соответствовать другой линии, противоположной ей относительно центра.
Симметрия имеет огромное значение в многих областях математики, таких как геометрия, алгебра, теория чисел и другие. Она позволяет нам рассматривать объекты и системы с точки зрения их внутренних структур и свойств, а также находить закономерности и установить взаимосвязи между ними. Без симметрии наш мир был бы гораздо более хаотичным и сложным для понимания.
Что такое симметрия в математике?
Симметрию можно представить как зеркальное отражение объекта относительно некоторой линии или плоскости. Если объект симметричен, то он остается неизменным после такого отражения. Например, плоская фигура считается симметричной, если она может быть разделена на две равные части, которые зеркально отражают друг друга.
Симметрия может быть различных видов. Одним из наиболее распространенных видов симметрии является осевая симметрия. Осевая симметрия проявляется в том, что фигура или объект остается неизменным после отражения относительно некоторой оси. Другим видом симметрии является центральная симметрия, которая проявляется в том, что фигура остается неизменной после поворота на 180 градусов относительно некоторой точки.
Симметрия в математике имеет множество примеров и применений. Она используется для анализа и классификации геометрических фигур, решения уравнений и задач алгебры, а также в ряде других математических задач и теорий. Изучение симметрии позволяет лучше понять и описать структуру и свойства объектов в математике.
Определение и основные понятия
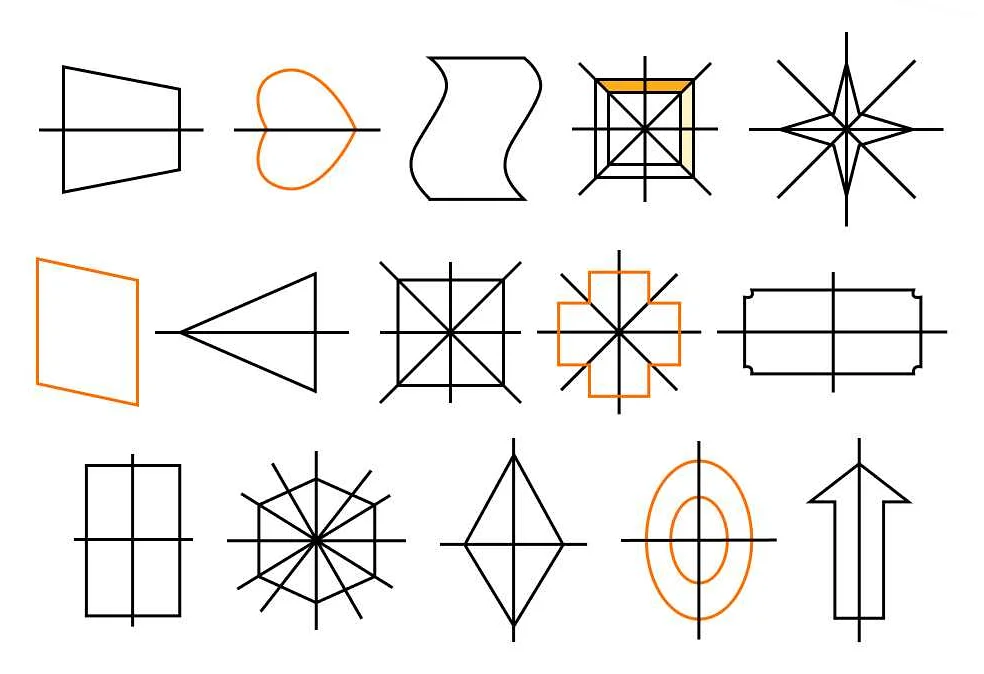
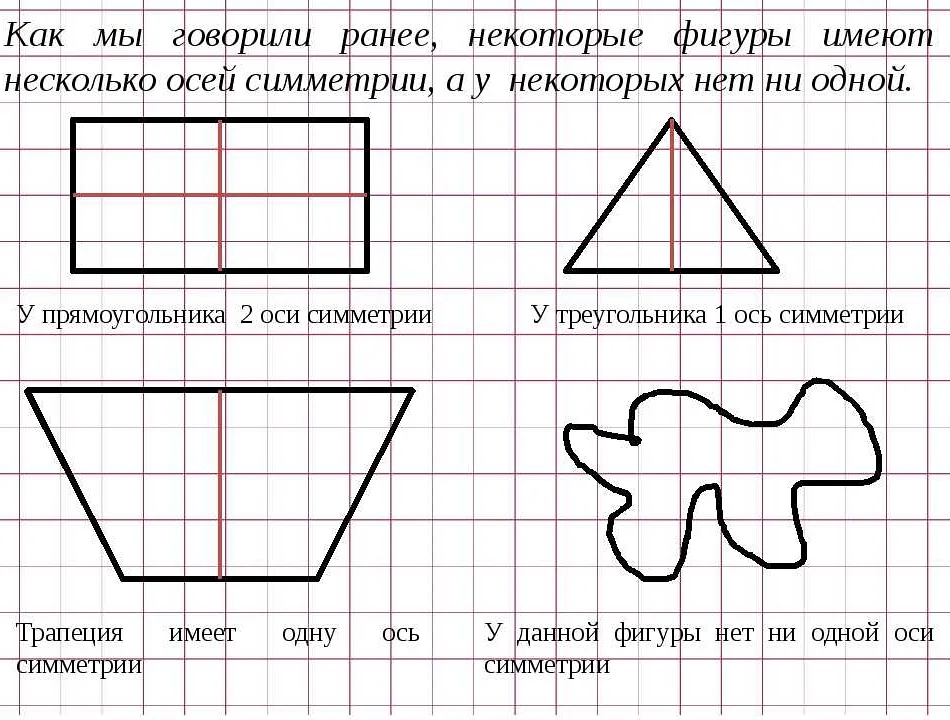
Одним из основных понятий в симметрии является ось симметрии. Она представляет собой линию или плоскость, которая делит фигуру на две равные части, которые отображают друг друга симметрично. Например, для прямоугольника ось симметрии проходит через его центр. Оси симметрии могут быть горизонтальными, вертикальными или диагональными.
Еще одним важным понятием в симметрии является точка симметрии. Это точка, через которую можно провести линию или плоскость симметрии. Например, для круга центр является точкой симметрии.
Виды симметрии включают:
- Осевую симметрию — фигура выглядит одинаково при отражении вдоль оси симметрии.
- Геометрическую симметрию — фигура выглядит одинаково при повороте на определенный угол.
- Трансляционную симметрию — фигура выглядит одинаково при сдвиге на определенное расстояние.
Симметрия в математике играет важную роль при изучении геометрии, алгебры и других разделов науки. Она помогает определить и классифицировать различные фигуры и структуры, а также облегчает решение различных задач и проблем.
Виды симметрии в математике
1. Осевая симметрия: в этом случае объект имеет ось симметрии, относительно которой он полностью симметричен. Это значит, что при отражении объекта относительно оси, его форма остается неизменной.
2. Плоская симметрия: объект имеет плоскость симметрии, относительно которой он симметричен. При отражении объекта относительно плоскости его форма остается неизменной.
3. Центральная симметрия: особый вид симметрии, при котором объект симметричен относительно центра. Любая прямая, проведенная через центр, делит объект на две симметричные части. При отражении объекта относительно центра его форма остается неизменной.
4. Комбинированная симметрия: некоторые объекты могут обладать одновременно несколькими видами симметрии, например, осевой и плоской симметрией.
Концепция симметрии играет важную роль в математике, а также находит применение в других науках и в повседневной жизни. Различные виды симметрии позволяют описывать и анализировать формы, структуры и законы природы.
Симметрия по отношению к прямой
При симметрии по отношению к прямой объект или фигура может быть разделена на две равные части с помощью прямой, которая является осью симметрии. Каждая точка на одной стороне прямой имеет симметричную точку на другой стороне прямой, отраженную относительно оси симметрии.
Симметрия по отношению к прямой встречается во многих геометрических фигурах и объектах. Например, прямоугольник, круг, треугольник и другие фигуры могут иметь симметрию по отношению к вертикальной или горизонтальной прямой.
Симметрия по отношению к прямой играет важную роль в геометрии, дизайне и искусстве. Она позволяет создавать симметричные и гармоничные композиции, которые воспринимаются как эстетически приятные. Также она помогает в решении задач по нахождению симметричных точек и фигур относительно заданной прямой.
Симметрия по отношению к точке
В математике точка, относительно которой происходит симметрия, называется центром симметрии. Все объекты, расположенные симметрично относительно этой точки, считаются симметричными.
Для определения симметричных объектов относительно выбранной точки можно провести лучи (прямые) из центра симметрии, которые попарно пересекаются с объектами. Если все пересечения находятся на одинаковом расстоянии от центра симметрии, то объекты считаются симметричными.
Симметрия по отношению к точке широко используется в геометрии для построения фигур и определения их свойств. Также она находит применение в изобразительном искусстве, где симметричные изображения создаются для достижения гармонии и эстетического эффекта.
Симметрия по отношению к плоскости
Плоскость симметрии представляет собой гипотетическую плоскость, которая делит фигуру на две симметричные части. Каждая точка в одной части фигуры симметрична соответствующей точке в другой части относительно плоскости симметрии.
Симметрия по отношению к плоскости может быть вертикальной, горизонтальной или наклонной. Вертикальная симметрия означает, что фигура сохраняет свою форму и размер при отражении относительно вертикальной плоскости. Горизонтальная симметрия подразумевает сохранение формы и размера при отражении относительно горизонтальной плоскости. Наклонная симметрия возникает, когда фигура сохраняет свою форму и размер при отражении относительно плоскости, которая наклонена под углом к горизонту.
Примером симметрии по отношению к плоскости может служить зеркальное отражение. Если взять зеркало и отразить в нем фигуру, то полученное отражение будет являться симметричным относительно зеркальной плоскости.
Симметрия по отношению к плоскости имеет широкое применение в геометрии, физике, биологии и других науках. Она помогает в анализе и классификации различных объектов, а также играет важную роль в искусстве и дизайне.
Примеры симметрии в математике

- Осевая симметрия: осевая симметрия означает, что фигура может быть разделена на две равные части относительно оси симметрии. Примером осевой симметрии является равнобедренный треугольник, у которого ось симметрии — это прямая, проходящая через вершину и середину основания треугольника.
- Центральная симметрия: центральная симметрия означает, что фигура может быть разделена на две равные части относительно центра симметрии. Примером центральной симметрии является окружность, у которой центр симметрии — это сам центр окружности.
- Симметрия относительно точки: некоторые фигуры могут быть симметричны относительно конкретной точки. Например, круг может быть симметричен относительно любой точки, находящейся на его окружности.
- Фрактальная симметрия: фракталы — это сложные геометрические фигуры, которые обладают симметрией на разных масштабах. Фракталы могут иметь самоподобие, когда маленькая часть фрактала выглядит как уменьшенная копия всего фрактала. Примером фрактальной симметрии является фрактал Мандельброта.
Это только некоторые примеры симметрии в математике. Симметрия является важным инструментом для изучения и понимания различных математических концепций и фигур.
Значение симметрии в различных областях
В физике симметрия играет важную роль при изучении фундаментальных законов природы. Например, законы сохранения энергии, импульса и момента имеют симметричные свойства, что позволяет сделать выводы о симметрии самой природы. Также симметрия используется при изучении кристаллических структур и оптических свойств материалов.
В химии симметрия помогает классифицировать молекулы и определять их свойства. Симметричные молекулы обладают особыми свойствами, например, они могут быть хиральными или иметь определенную оптическую активность. Изучение симметрии молекул позволяет улучшить процессы синтеза и создания новых материалов.
В биологии симметрия играет важную роль при изучении организмов. Многие животные и растения обладают симметричным строением, что помогает им в функционировании. Например, симметричность тела позволяет животным двигаться более эффективно и улучшает их размножение. Также симметрия используется при изучении генетических кодов и эволюции.
В искусстве симметрия часто используется для создания гармоничных и привлекательных композиций. Симметричные формы и узоры привлекают внимание зрителя и создают ощущение порядка и баланса. Симметричные композиции используются в архитектуре, дизайне, живописи и скульптуре.
В технологиях симметрия применяется для создания симметричных и сбалансированных конструкций. Например, в автомобильной промышленности симметричное расположение деталей может обеспечить более устойчивое и безопасное движение. Также симметрия используется при проектировании электронных схем, оптических систем и многих других технических решений.
Таким образом, симметрия имеет большое значение в различных областях, помогая нам лучше понять и описать мир вокруг нас, создавать красивые и функциональные объекты, а также разрабатывать новые технологии и материалы.
Вопрос-ответ:
Что такое симметрия в математике?
Симметрия в математике — это свойство фигуры или объекта сохранять свою форму и структуру при некоторых преобразованиях, таких как повороты, отражения или переносы.
Какие бывают виды симметрии в математике?
В математике существует несколько видов симметрии. Одним из них является осевая симметрия, когда фигура делится на две симметричные части относительно оси. Другим видом является центральная симметрия, когда фигура имеет центр, относительно которого она симметрична. Также существуют симметрия относительно плоскости и симметрия относительно точки.
Какие примеры симметрии можно привести?
Примеры симметрии можно найти вокруг нас. Например, лицо человека является симметричным относительно центральной оси — линии, проходящей через нос. Круг является симметричным относительно любого радиуса, а прямоугольник — относительно горизонтальной и вертикальной осей.
Какая роль симметрии в математике?
Симметрия играет важную роль в математике. Она помогает нам классифицировать и анализировать геометрические фигуры и объекты. Симметричные фигуры и структуры часто являются более простыми для изучения и понимания. Кроме того, симметрия используется в различных областях математики, таких как теория групп, топология, фракталы и другие.
Каким образом симметрия применяется в реальной жизни?
Симметрия имеет множество применений в реальной жизни. Например, симметричные фигуры и узоры используются в дизайне, архитектуре и искусстве. Отражение симметрии можно наблюдать в зеркале или в отражении водной поверхности. Симметричные структуры также играют важную роль в биологии, например, в строении растений и животных.
Что такое симметрия в математике?
Симметрия в математике — это свойство фигур, объектов или функций сохранять свою форму, размеры и расположение при определенных преобразованиях. Это означает, что после применения симметричного преобразования объект остается неизменным.
Какие бывают виды симметрии в математике?
В математике выделяют несколько видов симметрии. Это осевая симметрия, центральная симметрия и трансляционная симметрия. Осевая симметрия отражает фигуру относительно некоторой оси, центральная симметрия — относительно некоторой точки, а трансляционная симметрия сдвигает фигуру на некоторое расстояние без изменения ее формы.
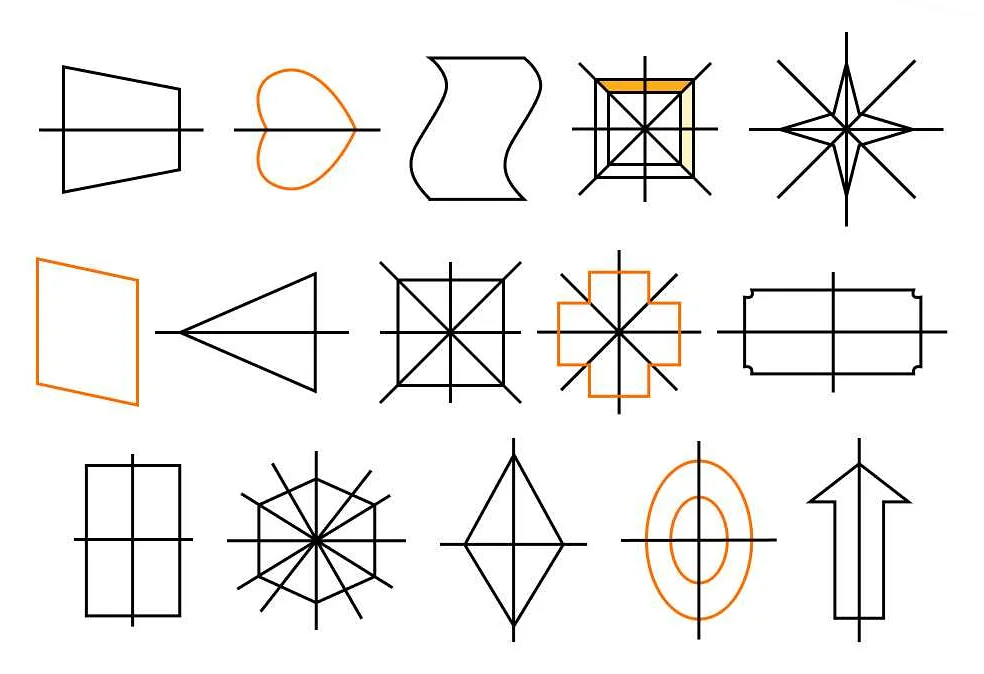
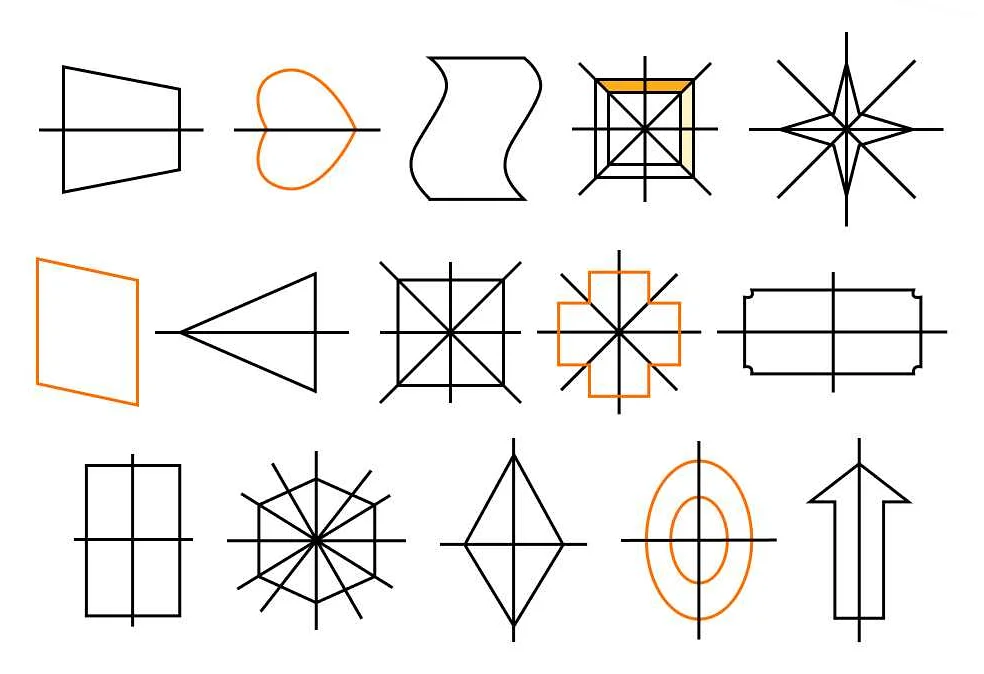
Статья очень интересная и познавательная! Симметрия в математике — это такая удивительная и прекрасная особенность, которая присутствует во многих объектах и явлениях. Я всегда был удивлен, как наши умные математики смогли вывести и изучить различные виды симметрии. Например, осевую симметрию можно найти в зеркале или даже в форме нашего лица. Также увлекательно узнавать о понятии плоской симметрии и ее проявлениях в геометрических фигурах. Все это делает математику еще более интересной и красивой наукой. Спасибо автору за прекрасное изложение темы! Жду с нетерпением новых статей об увлекательных математических концепциях.