Что такое скорость удаления в математике

Скорость удаления в математике — это показатель, указывающий на то, как быстро функция или переменная изменяется по отношению к другой переменной. Этот показатель является важным инструментом при изучении процессов изменения в математических моделях и может быть применен в различных областях, таких как физика, экономика и технические науки.

Скорость удаления — это понятие, которое используется в математике для описания того, как быстро функция или последовательность приближается к определенному значению или бесконечности. Она является важным инструментом для анализа поведения функций и их изменений в заданной точке или на бесконечности.

Определение скорости удаления включает в себя не только само значение, но и направление. Скорость может быть положительной или отрицательной, что указывает на приближение к значению справа или слева соответственно. Она также может быть равной нулю, что означает отсутствие изменений функции или последовательности в данной точке.

Пример 1:

Рассмотрим функцию f(x) = x^2. Если мы приближаемся к точке x = 2, то мы можем наблюдать, что при уменьшении значения x к 2, значения функции f(x) также приближаются к значению 4. Это означает, что скорость удаления функции f(x) при приближении к 2 положительна. С другой стороны, если мы приближаемся к точке x = -2, то значения функции f(x) также приближаются к значению 4, но с отрицательной скоростью удаления.

Знание скорости удаления позволяет нам более точно анализировать функции и последовательности, а также предсказывать их поведение в определенных точках. Это важное понятие, которое имеет множество применений в различных областях математики и ее приложений.

Определение скорости удаления

Скорость удаления может быть положительной или отрицательной, в зависимости от направления движения объекта. Положительная скорость удаления означает, что объект движется вперед, в то время как отрицательная скорость удаления указывает на движение назад.

Для измерения скорости удаления используется формула:

• Скорость удаления = (конечное положение — начальное положение) / время

В математике скорость удаления может быть применена в различных контекстах, таких как движение тела по прямой, движение по окружности или движение в трехмерном пространстве. Например, скорость удаления может быть использована для определения скорости автомобиля на прямой дороге или скорости спутника, движущегося по орбите вокруг Земли.

Что такое скорость удаления в математике

Скорость удаления может быть положительной или отрицательной, в зависимости от направления приближения. Если скорость удаления положительна, это означает, что функция или последовательность приближается к пределу с увеличением независимой переменной. Если скорость удаления отрицательна, это означает, что функция или последовательность приближается к пределу с уменьшением независимой переменной.

Например, рассмотрим функцию f(x) = 2x + 1. В данном случае скорость удаления будет равна 2, так как с увеличением значения x на единицу, значение функции увеличивается на 2. То есть, функция приближается к пределу (если он существует) со скоростью 2.

Скорость удаления в математике играет важную роль при анализе функций и последовательностей. Она позволяет определить, насколько быстро функция или последовательность приближаются к некоторому значению и как это изменяется в зависимости от изменения независимой переменной.

Как вычислить скорость удаления

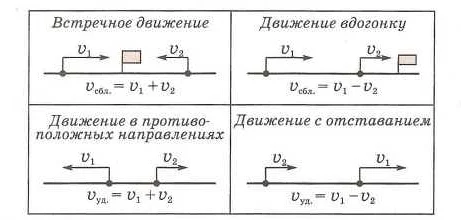
Чтобы вычислить скорость удаления, необходимо использовать следующую формулу:

Скорость удаления = (Конечное положение — Начальное положение) / Время

Здесь:

• Конечное положение — это положение объекта после определенного времени;
• Начальное положение — это положение объекта в начальный момент времени;
• Время — это интервал времени, за которое объект переместился.

Например, предположим, что объект начинает движение из точки А и через 5 секунд достигает точки В. Если начальное положение объекта А равно 10 метрам, а конечное положение объекта В равно 30 метрам, то скорость удаления можно вычислить следующим образом:

Скорость удаления = (30 м — 10 м) / 5 с = 4 м/с

Таким образом, скорость удаления объекта составляет 4 метра в секунду.

Примеры скорости удаления

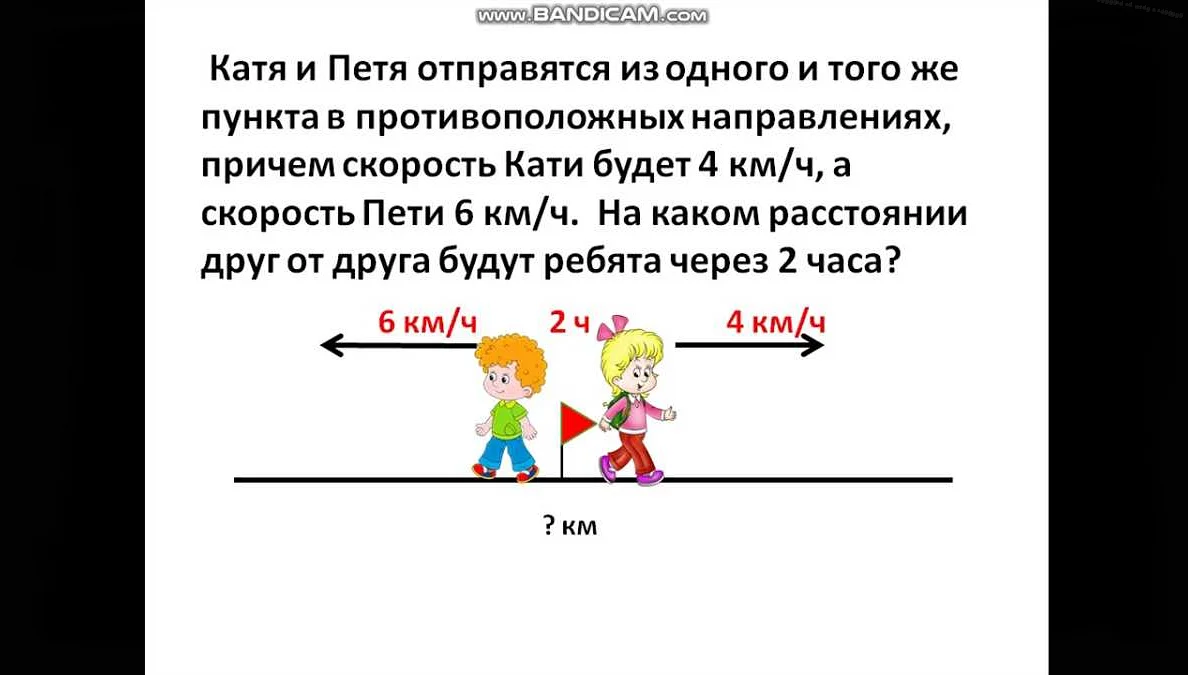
ПримерФункция или последовательностьСкорость удаления

1	f(x) = 1/x	Линейная скорость удаления
2	f(x) = 1/x^2	Квадратичная скорость удаления
3	f(n) = 1/n	Линейная скорость удаления
4	f(n) = 1/n^2	Квадратичная скорость удаления

В первом примере функция f(x) = 1/x приближается к нулю линейно, так как при увеличении значения аргумента x вдвое, значение функции уменьшается вдвое.

Во втором примере функция f(x) = 1/x^2 приближается к нулю квадратично, так как при увеличении значения аргумента x вдвое, значение функции уменьшается вчетверо.

Аналогичные примеры можно рассмотреть для последовательностей. Например, последовательность f(n) = 1/n приближается к нулю линейно, а последовательность f(n) = 1/n^2 приближается к нулю квадратично.

Знание скорости удаления позволяет более точно оценить поведение функции или последовательности и использовать это знание в различных математических и научных задачах.

Пример 1: Удаление скорости автомобилем

Рассмотрим ситуацию, когда автомобиль движется по прямой дороге с постоянной скоростью. Пусть начальное положение автомобиля равно x₀, а его скорость равна v₀.

После некоторого времени t автомобиль будет находиться на расстоянии x = x₀ + v₀t от начального положения. Другими словами, за время t автомобиль переместится на расстояние, пропорциональное скорости и времени.

Таким образом, скорость удаления автомобилем в данном случае определяется как расстояние, пройденное автомобилем за единицу времени.

Пример: Если автомобиль движется со скоростью 60 км/ч, то за 1 час он удалится от начального положения на 60 км.

Описанный пример иллюстрирует понятие скорости удаления в математике и позволяет лучше понять его смысл и применение.

Пример 2: Удаление скорости тела в свободном падении

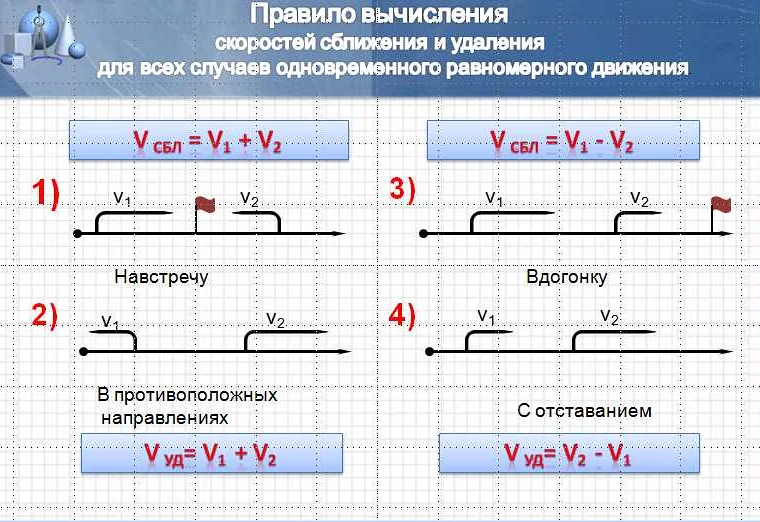
Предположим, что у нас есть тело, которое движется вниз по вертикальной оси в свободном падении. В начальный момент времени тело имеет некоторую начальную скорость. Задача состоит в том, чтобы определить, как изменяется скорость тела по мере его движения вниз.

Для решения этой задачи мы можем использовать уравнение движения для свободного падения:

$$v = v_0 + gt$$

Где:

• $$v$$ — скорость тела в данный момент времени;
• $$v_0$$ — начальная скорость тела;
• $$g$$ — ускорение свободного падения (приблизительно равно 9.8 м/с²);
• $$t$$ — время, прошедшее с начального момента.

Из этого уравнения видно, что скорость тела увеличивается на ускорение свободного падения, умноженное на время. Таким образом, скорость тела будет увеличиваться с течением времени.

Например, пусть начальная скорость тела равна 0 м/с, а время равно 2 секунды. Подставим эти значения в уравнение:

$$v = 0 + 9.8 \cdot 2 = 19.6 \, \text{м/с}$$

Таким образом, через 2 секунды скорость тела в свободном падении будет составлять 19.6 м/с.

Вопрос-ответ:

Что такое скорость удаления в математике?

Скорость удаления в математике — это показатель, определяющий, насколько быстро или медленно объект удаляется или приближается к другому объекту или точке в пространстве.

Как определить скорость удаления?

Скорость удаления определяется путем измерения изменения расстояния между двумя объектами в единицу времени. Для этого измеряется исходное расстояние между объектами и время, за которое объекты приближаются или удаляются друг от друга. Затем расстояние делится на время, чтобы получить скорость удаления.

Какие есть примеры скорости удаления в математике?

Примеры скорости удаления в математике могут включать движение автомобиля, движение планет, скорость расширения Вселенной и даже изменение расстояния между двумя людьми, идущими в противоположных направлениях.

Какую формулу можно использовать для вычисления скорости удаления?

Для вычисления скорости удаления можно использовать формулу: скорость удаления = изменение расстояния / изменение времени. Например, если расстояние между двумя объектами увеличивается на 10 метров за 5 секунд, то скорость удаления будет равна 2 метра в секунду.

Зачем нужно изучать скорость удаления в математике?

Изучение скорости удаления в математике позволяет нам более точно описывать и понимать движение и изменение объектов в пространстве. Это полезно в физике, астрономии, технике и других областях, где важно знать, насколько быстро объекты приближаются или удаляются друг от друга.

Что такое скорость удаления в математике?

Скорость удаления в математике — это показатель, который позволяет определить, насколько быстро или медленно объект или процесс удаляется от исходной точки. Это может быть представлено в виде скорости движения точки на координатной плоскости или в пространстве.

Как вычислить скорость удаления?

Чтобы вычислить скорость удаления, необходимо знать начальные координаты объекта и его конечные координаты, а также время, за которое произошло перемещение. Скорость удаления вычисляется путем деления разности конечных и начальных координат на время перемещения.

Практическое применение скорости удаления

В физике скорость удаления используется, например, для изучения движения тела. Зная скорость удаления, можно определить время, за которое объект достигнет определенной позиции или пройдет определенное расстояние. Это позволяет предсказать его дальнейшее движение и оптимизировать процессы.

В экономике скорость удаления может быть использована для анализа изменения цен на товары или услуги. Зная скорость изменения цен, можно прогнозировать и адаптировать бизнес-стратегии, принимать решения о закупке или продаже товаров, а также устанавливать цены на товары и услуги.

В биологии скорость удаления используется для изучения различных процессов, таких как рост организмов, размножение популяций или распространение болезней. Зная скорость удаления, можно оценить эффективность лечения, прогнозировать изменение популяции или оценить влияние окружающей среды на живые организмы.

Таким образом, скорость удаления имеет широкое практическое применение в различных областях науки и помогает в анализе и оптимизации различных процессов.

Видео по теме: