Что такое скорость сближения в математике
Содержимое
- 1 Что такое скорость сближения в математике
- 1.1 Скорость сближения в математике: общая информация
- 1.2 Что такое скорость сближения в математике?
- 1.3 Зачем нужно изучать скорость сближения?
- 1.4 Примеры скорости сближения
- 1.5 Как рассчитать скорость сближения?
- 1.6 Практическое применение скорости сближения
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Что такое скорость сближения в математике?
- 1.8.0.2 Какая формула используется для вычисления скорости сближения?
- 1.8.0.3 Можете привести примеры использования скорости сближения в математике?
- 1.8.0.4 Как можно интерпретировать результат вычисления скорости сближения?
- 1.8.0.5 Как скорость сближения связана с понятием предела функции?
- 1.9 Как улучшить скорость сближения?
- 1.10 Выводы
Скорость сближения в математике — это понятие, которое отражает изменение величины или значения функции с течением времени или другой переменной. Узнайте, как определить и измерить скорость сближения и как она применяется в различных областях математики.
Скорость сближения в математике — это понятие, которое описывает, насколько быстро две или более величины приближаются друг к другу. В математических задачах, где необходимо рассмотреть, как одна величина приближается к другой, скорость сближения является важным фактором для определения точности и эффективности решения.
Чтобы лучше понять, что такое скорость сближения, рассмотрим пример. Представим, что у нас есть последовательность чисел, начиная с 1 и увеличивающихся на 2 с каждым последующим числом: 1, 3, 5, 7, 9 и т.д. Мы можем заметить, что каждое последующее число приближается к предыдущему числу с «скоростью» 2.
Скорость сближения в данном примере равна 2, так как каждое последующее число увеличивается на 2.
Теперь предположим, что у нас есть другая последовательность чисел, начиная с 1 и увеличивающихся в два раза с каждым последующим числом: 1, 2, 4, 8, 16 и т.д. В этом случае скорость сближения будет равна 2, так как каждое последующее число увеличивается в два раза по сравнению с предыдущим числом.
Таким образом, скорость сближения в математике позволяет определить, насколько быстро две величины приближаются друг к другу и как они зависят друг от друга. Понимание этого понятия может помочь в решении различных математических задач и проблем.
Скорость сближения в математике: общая информация
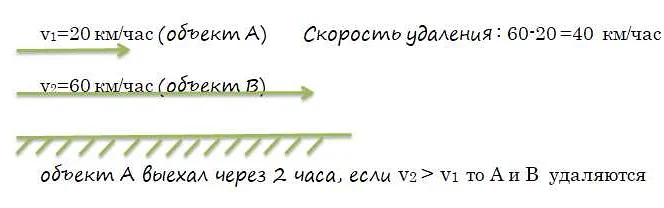
В математике скорость сближения может быть выражена численно или символически. Численное выражение скорости сближения позволяет определить конкретное значение, например, скорость сближения двух чисел. Символическое выражение используется для описания общего поведения объектов или функций.
Скорость сближения в математике может иметь различные формы и зависит от конкретной задачи или предметной области. Например, скорость сближения может описывать как изменение расстояния между двумя точками, так и изменение значений функции с течением времени.
Одной из основных задач, связанных со скоростью сближения, является оценка ее значения. Для этого могут применяться различные методы и инструменты, такие как дифференцирование, интегрирование, анализ границы и другие.
Понимание скорости сближения является важным для решения множества математических задач и проблем. Она позволяет определить, насколько быстро или медленно объекты или значения приближаются друг к другу, а также предсказать их будущее поведение.
ПримерОписание
| 1 | Пример описания скорости сближения двух точек на плоскости |
| 2 | Пример описания скорости сближения последовательности чисел |
| 3 | Пример описания скорости сближения графика функции |
Что такое скорость сближения в математике?
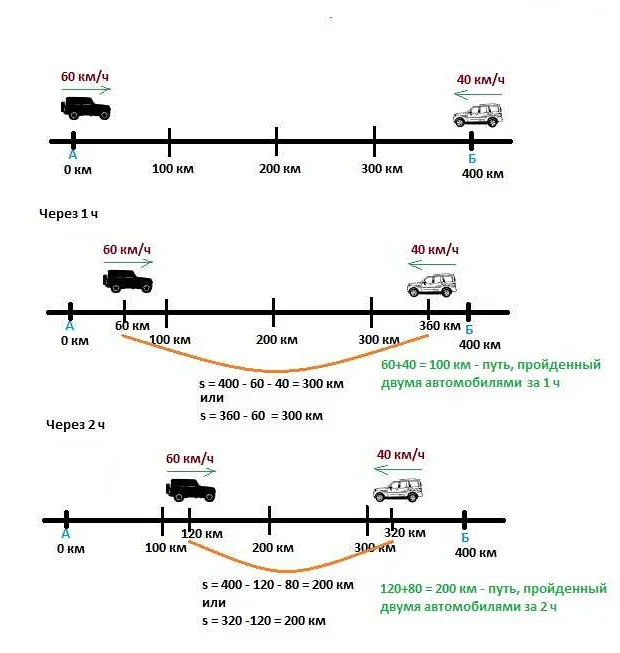
Скорость сближения в математике относится к понятию предела функции. Она описывает, как быстро значения функции приближаются к определенному числу или точке, когда аргумент функции приближается к определенному значению или точке.
Математически скорость сближения можно определить следующим образом: если для каждого положительного числа ε существует положительное число δ, такое что для всех x из области определения функции, для которых 0 < |x — a| < δ, выполнено |f(x) — L| < ε, где a — предельное значение и L — предел функции при x стремящемся к a, то говорят, что функция имеет скорость сближения к пределу L при x стремящемся к a.
Примеры скорости сближения в математике включают линейную, квадратичную и экспоненциальную скорость сближения. Линейная скорость сближения означает, что значения функции приближаются к пределу с постоянной скоростью. Квадратичная скорость сближения означает, что значения функции приближаются к пределу быстрее, чем линейно. Экспоненциальная скорость сближения означает, что значения функции приближаются к пределу с ростом экспоненты.
Скорость сближения в математике является важным понятием при изучении пределов функций. Она помогает определить, как быстро функция приближается к определенному значению и может быть использована для анализа поведения функций и решения различных проблем.
Зачем нужно изучать скорость сближения?
Знание скорости сближения позволяет нам предсказывать, как быстро система или явление достигнет определенного состояния или значения. Это особенно полезно, когда мы работаем с динамическими моделями, например, в физике, экономике или биологии.
Изучение скорости сближения также помогает нам анализировать и сравнивать различные процессы и явления. Мы можем определить, какой из них происходит быстрее или медленнее, что помогает нам принимать решения и делать выводы о наших исследованиях и экспериментах.
Также изучение скорости сближения позволяет нам определить, является ли процесс сходящимся или расходящимся. Сходящиеся процессы имеют конечное предельное значение, в то время как расходящиеся процессы не имеют предельного значения.
В целом, изучение скорости сближения помогает нам лучше понять и описывать мир вокруг нас, предсказывать его эволюцию и принимать обоснованные решения на основе наших наблюдений и анализа данных.
Примеры скорости сближения
Приведем несколько примеров, чтобы более наглядно представить, что такое скорость сближения:
ПримерСкорость сближения
| Пример 1 | Линейная |
| Пример 2 | Квадратичная |
| Пример 3 | Экспоненциальная |
В каждом примере скорость сближения может быть разной и зависит от конкретной ситуации. Линейная скорость означает, что две величины приближаются друг к другу с постоянной скоростью. Квадратичная скорость обозначает, что расстояние между величинами уменьшается квадратично, то есть быстрее с увеличением времени. Экспоненциальная скорость означает, что расстояние между величинами уменьшается экспоненциально, что говорит о очень быстром сближении.
Таким образом, понимание скорости сближения позволяет более точно анализировать и предсказывать изменения величин в математике и других областях науки.
Как рассчитать скорость сближения?
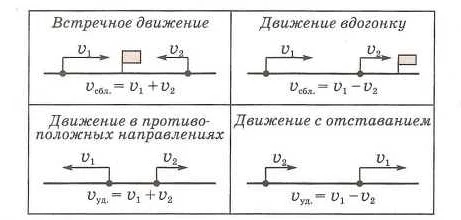
Скорость сближения в математике представляет собой показатель изменения расстояния между двумя объектами или точками в пространстве. Для рассчёта скорости сближения необходимо знать начальное и конечное расстояние между объектами, а также время, за которое произошло изменение расстояния.
Формула для расчёта скорости сближения выглядит следующим образом:
Скорость сближения = (Конечное расстояние — Начальное расстояние) / Время
Например, предположим, что объект A находится на расстоянии 10 метров от объекта B. Через 5 секунд расстояние между ними сократилось до 5 метров. Чтобы рассчитать скорость сближения, мы можем использовать следующие значения:
Начальное расстояние = 10 метров
Конечное расстояние = 5 метров
Время = 5 секунд
Подставив эти значения в формулу, получим:
Скорость сближения = (5 метров — 10 метров) / 5 секунд
Скорость сближения = -1 метр/секунду
Ответ будет отрицательным, так как расстояние между объектами уменьшилось. Таким образом, скорость сближения составляет 1 метр в секунду.
Практическое применение скорости сближения
Одним из основных применений скорости сближения является расчет производных функций. Производная показывает, как быстро значение функции меняется в зависимости от изменения аргумента. Зная скорость сближения, можно вычислить производную и, тем самым, получить информацию о поведении функции.
Еще одним примером применения скорости сближения является задача о расстоянии. Если два объекта движутся навстречу друг другу, и мы знаем их скорости, то можно вычислить, через какое время они встретятся. Скорость сближения в данном случае позволяет найти время встречи.
Скорость сближения также используется при решении задач о предельных значениях. Предельное значение функции показывает, к чему стремится функция при приближении аргумента к определенной точке. Зная скорость сближения, можно определить, сходится ли функция к предельному значению и насколько быстро это происходит.
Таким образом, скорость сближения играет важную роль в различных областях математики и науки, позволяя анализировать и предсказывать поведение переменных и функций. Понимание этого понятия помогает решать разнообразные задачи и делает математику более применимой в реальной жизни.
Видео по теме:
Вопрос-ответ:
Что такое скорость сближения в математике?
Скорость сближения в математике — это концепция, которая описывает, насколько быстро две величины приближаются друг к другу. В математических терминах скорость сближения определяется как предел отношения изменения одной величины к изменению другой величины.
Какая формула используется для вычисления скорости сближения?
Формула для вычисления скорости сближения зависит от конкретной задачи. В некоторых случаях она может быть представлена как производная функции, описывающей изменение величины по времени. В других случаях формула может быть определена в терминах предела. В общем случае, скорость сближения вычисляется как отношение изменения одной величины к изменению другой.
Можете привести примеры использования скорости сближения в математике?
Конечно! Одним из примеров использования скорости сближения является вычисление предела функции. Если функция приближается к определенному значению при изменении аргумента, то скорость сближения определяет, насколько быстро это происходит. Также скорость сближения используется при решении задач на оптимизацию, где необходимо найти максимальную или минимальную скорость изменения некоторой величины.
Как можно интерпретировать результат вычисления скорости сближения?
Результат вычисления скорости сближения можно интерпретировать как меру изменения одной величины относительно изменения другой. Если результат положительный, то величина увеличивается по мере изменения другой величины. Если результат отрицательный, то величина уменьшается по мере изменения другой величины. Если результат равен нулю, то величина не изменяется при изменении другой величины.
Как скорость сближения связана с понятием предела функции?
Скорость сближения и предел функции тесно связаны друг с другом. Предел функции можно рассматривать как скорость сближения функции к определенному значению приближения аргумента к некоторому значению. Если предел функции существует, то скорость сближения стремится к нулю. Если предел не существует, то скорость сближения может быть положительной или отрицательной, в зависимости от направления приближения.
Как улучшить скорость сближения?

Скорость сближения в математике может быть улучшена с помощью нескольких методов и стратегий. Вот некоторые из них:
- Использование метода Ньютона. Этот метод позволяет быстро находить корни уравнений и улучшает скорость сближения. Он основан на итерационных вычислениях и использует производные функции для нахождения более точных приближений.
- Использование итерационных методов. Это методы, которые используют последовательные итерации для приближенного нахождения решений уравнений. Они могут быть основаны на различных алгоритмах, таких как метод простой итерации или метод Зейделя.
- Улучшение точности вычислений. Использование более точных вычислений, таких как использование большего числа знаков после запятой или использование высокоточных чисел (например, BigDecimal в Java), может значительно улучшить скорость сближения.
- Улучшение начального приближения. Если начальное приближение близко к истинному значению, то скорость сближения будет выше. Поэтому важно выбрать хорошее начальное приближение, основываясь на знании о функции и ее поведении.
- Использование параллельных вычислений. Если вычисления можно распараллелить, то это может значительно улучшить скорость сближения. Например, можно использовать несколько потоков или распределенные вычисления, чтобы ускорить процесс.
Важно отметить, что эти методы и стратегии могут различаться в зависимости от конкретной задачи и условий. Выбор оптимального подхода требует анализа и экспериментов для каждой конкретной ситуации.
Выводы
Скорость сближения может быть выражена с помощью различных математических инструментов, таких как пределы, производные и интегралы. Она играет важную роль в решении различных задач и проблем, связанных с изменением и приближением величин.
Примеры использования скорости сближения можно найти в различных областях математики, физики, экономики и других науках. Например, она может быть применена для определения скорости роста популяции, изменения стоимости товаров, движения тела и многих других явлений.
Выводы, сделанные на основе скорости сближения, могут быть полезными для анализа и прогнозирования различных процессов и явлений. Понимание этого понятия и его применение может помочь в решении сложных задач и развитии новых математических моделей и теорий.
Таким образом, скорость сближения является важным и полезным понятием в математике, которое позволяет изучать и анализировать различные процессы и явления, связанные с изменением величин.
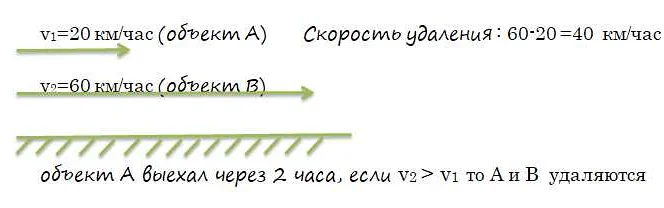
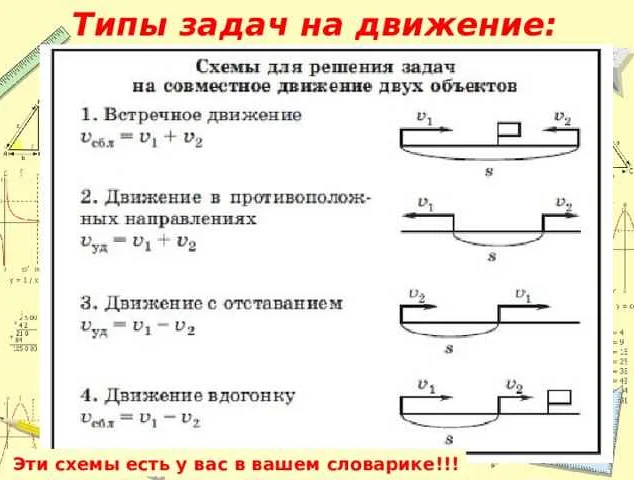

Статья очень понятно объясняет, что такое скорость сближения в математике. Я всегда думала, что это сложное понятие, но автор смог простыми словами и примерами раскрыть эту тему. Очень интересно узнать, что скорость сближения описывает, насколько быстро две величины или функции приближаются друг к другу. Понравилось, как автор привел примеры из реальной жизни, чтобы наглядно показать, как это работает. Статья дала мне полное представление о скорости сближения и теперь я готова применять эту концепцию в своих математических задачах. Спасибо за простое и понятное объяснение!