Что такое слагаемое слагаемое сумма в математике

Слагаемое — это числовое значение, которое складывается с другими слагаемыми для получения итоговой суммы. В математике слагаемые являются основными элементами при выполнении операций сложения. Узнайте, как слагаемые используются в математических вычислениях и как они влияют на общую сумму.

В математике слагаемое — это одно из чисел или выражений, которые складываются для получения суммы. Слагаемые могут быть положительными или отрицательными и могут содержать операции сложения, вычитания, умножения или деления. Слагаемое может также быть переменной или уравнением. Важно понимать, что слагаемые могут быть как частью простого арифметического выражения, так и сложного математического уравнения.

Сумма — это результат сложения двух или более слагаемых. Она представляет собой общую величину, полученную путем объединения всех слагаемых. Сумма может быть положительной, отрицательной или нулевой, в зависимости от знаков и значений слагаемых. В математике суммируются числа, выражения и уравнения, чтобы получить общую величину или решение.

Например, если у нас есть уравнение 2x + 3y = 10, то слагаемыми будут 2x и 3y, а сумма — 10. Если у нас есть простое арифметическое выражение 5 + 7 — 3, то слагаемыми будут 5, 7 и -3, а сумма будет равна 9.

Понимание понятий слагаемого и суммы является важным в математике, поскольку эти концепции используются во многих областях, включая алгебру, геометрию, физику и экономику. Они являются основой для решения уравнений, проведения вычислений и анализа данных. Знание этих понятий поможет вам разобраться в сложных математических задачах и улучшить вашу математическую подготовку.

Что такое слагаемое и сумма в математике

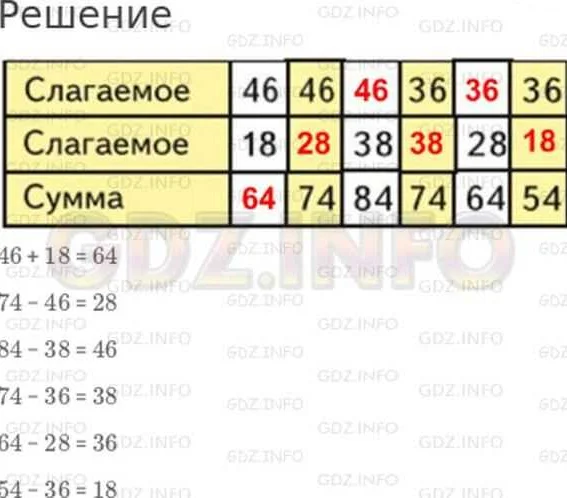
В математике слагаемыми называются числа или выражения, которые складываются для получения суммы. Слагаемые могут быть как положительными, так и отрицательными.

Сумма же представляет собой результат сложения всех слагаемых. Она также может быть положительной, отрицательной или равной нулю.

Например, в выражении 3 + 4 = 7, числа 3 и 4 являются слагаемыми, а число 7 — суммой.

Однако, слагаемые и сумма могут быть не только числами, но и выражениями. Например, в выражении (2 + 3) + (4 + 5) = 14, выражения (2 + 3) и (4 + 5) являются слагаемыми, а число 14 — суммой.

Сумма может быть также представлена в виде математической формулы, используя знак суммы ∑ (сумма n слагаемых от i=1 до n). Например, ∑(3 + 4) = 7.

Важно отметить, что порядок слагаемых в выражении может влиять на результат сложения. Например, в выражении 3 + 4 + 5 = 12, если поменять местами слагаемые 4 и 5, получится выражение 3 + 5 + 4 = 12.

ПримерыСлагаемыеСумма

2 + 3	2, 3	5
(7 + 8) + 9	7 + 8, 9	24
4 + (-3)	4, -3	1
∑(1 + 2 + 3)	1, 2, 3	6

Видео по теме:

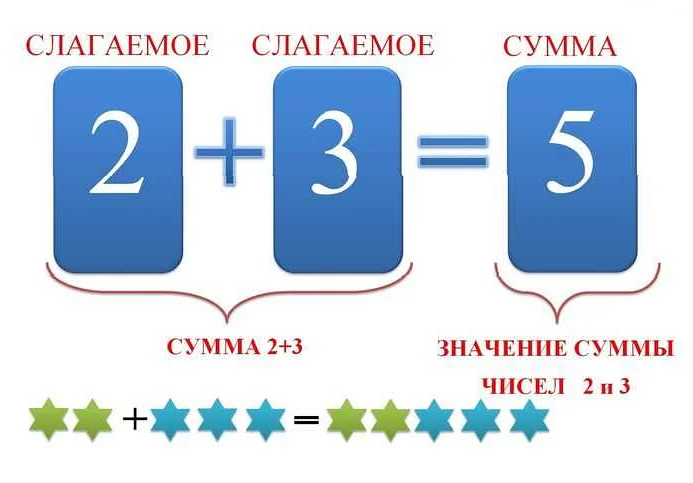
Понятие слагаемого

Например, в выражении 2 + 3, числа 2 и 3 являются слагаемыми. В этом случае, слагаемые 2 и 3 складываются для получения суммы, которая равна 5.

Слагаемое может быть любым числом — положительным, отрицательным или нулем. Они могут быть также представлены в виде переменных или алгебраических выражений.

Например, в выражении а + b, a и b являются слагаемыми. В этом случае, слагаемые a и b могут быть числами, переменными или алгебраическими выражениями, такими как 2x или 3y. Они могут быть сложены для получения суммы, которая зависит от конкретных значений a и b или переменных x и y.

Изучение понятия слагаемого имеет важное значение в математике, так как оно является основой для выполнения сложения и других арифметических операций. Понимание слагаемых помогает нам разбираться с основами математики и решать различные задачи на сложение и вычисление суммы.

Определение слагаемого

Слагаемые могут быть положительными или отрицательными числами. Положительные слагаемые увеличивают общую сумму, а отрицательные слагаемые уменьшают ее. Например, в выражении 5 + (-3) + 2, число 5 и число 2 являются положительными слагаемыми, так как они увеличивают сумму, а число -3 является отрицательным слагаемым, так как оно уменьшает сумму.

Слагаемые могут быть представлены в виде таблицы, где каждое слагаемое указано в отдельной ячейке. Например, в таблице ниже представлены слагаемые для выражения 4 + 6 + (-2):

Слагаемое 1Слагаемое 2Слагаемое 3

4

6

-2

Вопрос-ответ:

Что такое слагаемое в математике?

Слагаемое — это число или выражение, которые складываются вместе для получения суммы. Например, в выражении 2 + 3, числа 2 и 3 являются слагаемыми.

Как определить сумму в математике?

Сумма — это результат сложения двух или большего числа слагаемых. Она представляет собой общее количество или общую величину, полученную путем объединения слагаемых. Например, сумма чисел 2, 3 и 4 равна 9.

Можешь дать пример слагаемого?

Конечно! В выражении 5 + 7, числа 5 и 7 являются слагаемыми.

Как можно представить сумму в виде выражения?

Сумму можно представить в виде выражения, используя знак «+». Например, сумма чисел 3 и 5 можно записать как 3 + 5.

Можно ли сложить разные типы чисел?

Да, можно сложить различные типы чисел. Например, можно сложить целое число и десятичную дробь. Но учтите, что результат может быть в другом типе числа.

Примеры слагаемых

• 4
• 7
• 2x
• 3y
• 9z2

В примерах выше, каждое число или выражение является слагаемым, которое может быть складывано с другими слагаемыми для получения суммы. Например, 4 + 7 = 11, где 4 и 7 — слагаемые, а 11 — их сумма.

Слагаемые могут быть любыми числами или выражениями, включая переменные, степени, корни и другие математические операции. Важно помнить, что слагаемые могут быть как положительными, так и отрицательными.

Понятие суммы

Сумма может состоять из любого количества слагаемых. Например, если у нас есть слагаемые 2, 4 и 6, то их сумма будет равна 12.

Сумма также может быть выражена с помощью алгебраического выражения. Например, сумма выражения 3x + 2y и выражения 4x — y будет равна 7x + y.

Сумма может иметь различные свойства, например, коммутативность и ассоциативность. Коммутативность означает, что порядок слагаемых не влияет на результат суммы. Например, сумма чисел 2 и 3 будет равна сумме чисел 3 и 2. Ассоциативность означает, что результат суммы не зависит от того, какие слагаемые сгруппированы в скобки. Например, сумма чисел (2 + 3) + 4 будет равна сумме чисел 2 + (3 + 4).

Определение суммы

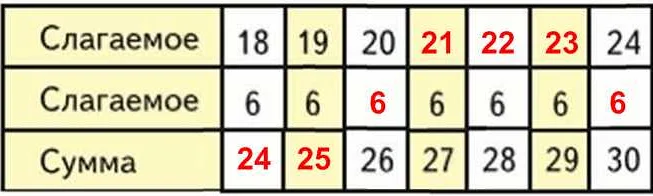
Сумма может быть как конечной, так и бесконечной. Конечная сумма получается при сложении конечного числа слагаемых, например, 2 + 3 + 5 = 10. Бесконечная сумма возникает при сложении бесконечного числа слагаемых, например, 1 + 1/2 + 1/4 + 1/8 + … = 2.

Сумма может быть как положительной, так и отрицательной. Положительная сумма получается при сложении положительных слагаемых, например, 3 + 4 + 2 = 9. Отрицательная сумма получается при сложении отрицательных слагаемых, например, -2 + (-5) + (-3) = -10.

Сумма может быть выражена не только числами, но и алгебраическими выражениями или функциями. Например, сумма двух алгебраических выражений (x + y) + (2x — 3y) = 3x — 2y.

Сумма является основным понятием в математике и широко используется в различных областях, таких как арифметика, алгебра, геометрия и теория вероятностей.

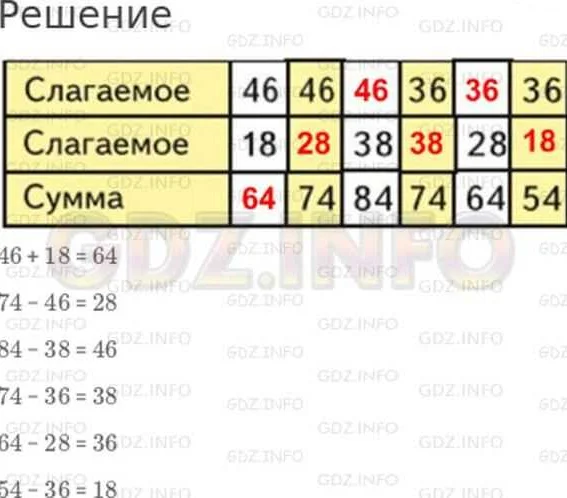
Примеры суммы

1. Сумма 5 и 3 равна 8.
2. Сумма 2, 4 и 6 равна 12.
3. Сумма 10, 20, 30 и 40 равна 100.
4. Сумма -7 и 7 равна 0 (отрицательное число и его абсолютное значение).
5. Сумма десяти чисел, начиная с 1 и заканчивая 10, равна 55 (сумма арифметической прогрессии).

Сумма может быть вычислена для любого количества слагаемых и может включать как положительные, так и отрицательные числа. Вычисление суммы является одной из основных операций в математике и имеет широкий спектр применений в различных областях.