Что такое slope в математике

Slope в математике — это показатель, определяющий наклон прямой. Узнайте, как вычислить slope и его значение в геометрии и алгебре. Исследуйте его применение в различных задачах и понимание его значения в контексте графиков и функций.

Склон, или slope, является одним из фундаментальных понятий в математике, которое имеет широкое применение в различных областях. Склон — это мера изменения величины одной переменной относительно другой переменной. Он описывает, как меняется зависимая переменная при изменении независимой переменной.

Склон обычно обозначается буквой m и выражается числовым значением. Он может быть положительным, отрицательным или нулевым. Положительный склон означает, что зависимая переменная увеличивается при увеличении независимой переменной, отрицательный склон указывает на уменьшение зависимой переменной при увеличении независимой переменной, а нулевой склон указывает на отсутствие зависимости между переменными.

Применение склона в математике очень разнообразно. Он используется, например, для определения наклона прямой на координатной плоскости, вычисления скорости тела в физике, анализа трендов и предсказания будущих значений в экономике, исследования градиента в геометрии и многое другое.

Понимание понятия склона позволяет анализировать и предсказывать различные явления и процессы. Оно является неотъемлемой частью алгебры, геометрии, физики, экономики и других наук. Изучение склона помогает развить абстрактное мышление, логическое мышление и навыки анализа данных.

Определение и основные понятия

Основными понятиями, связанными с понятием slope, являются:

• Наклон: это мера измерения угла, под которым прямая линия восходит или опускается. Наклон может быть положительным (прямая идет вверх), отрицательным (прямая идет вниз) или нулевым (прямая горизонтальна).
• Коэффициент наклона: это числовое значение, которое определяет, насколько быстро или медленно меняется зависимая переменная в зависимости от изменения независимой переменной. Коэффициент наклона может быть вычислен по формуле.
• Точка наклона: это точка, через которую проходит прямая линия, имеющая заданный наклон. Она может быть использована для построения линейной функции или для определения изменений величин.

Важно отметить, что понятие

slope широко используется в различных областях, таких как геометрия, физика, экономика и другие. Оно является важным инструментом для анализа и интерпретации данных и помогает в понимании взаимосвязей и трендов в исследуемых явлениях.

Видео по теме:

Геометрическая интерпретация

Если угол склона положительный, это означает, что прямая наклонена вверх, справа налево. Если угол склона отрицательный, это означает, что прямая наклонена вниз, слева направо. Если угол склона равен нулю, это означает, что прямая горизонтальна.

Склон также может быть использован для определения направления и интенсивности изменения. Чем больше абсолютное значение склона, тем круче наклон прямой и тем быстрее изменяется зависимая переменная.

Физическое значение slope

В физике понятие slope, или угловой коэффициент, играет важную роль при изучении зависимости между различными физическими величинами. Склон, или наклон, графика функции в точке может быть интерпретирован как физическое значение, которое характеризует изменение одной величины относительно другой.

Например, в механике slope может означать скорость изменения положения тела с течением времени, а в термодинамике — температурный градиент. Также, в электротехнике slope может представлять собой электрическое напряжение или ток, а в оптике — оптическую плотность или коэффициент преломления.

Использование понятия slope позволяет установить качественную и количественную связь между различными физическими величинами, а также определить взаимосвязь между различными процессами или явлениями.

В итоге, физическое значение slope является важным инструментом для анализа физических закономерностей и моделирования физических процессов в различных областях науки и техники.

Применение в алгебре и анализе

В алгебре склонность используется для нахождения угла наклона прямой и его влияния на функцию. Например, если склонность прямой положительна, то функция возрастает, а если отрицательна, то функция убывает. Склонность также может быть использована для нахождения тангенса угла наклона прямой, что помогает понять, насколько быстро функция меняется.

В анализе склонность используется для нахождения производной функции. Производная показывает, как быстро функция меняется в определенной точке. Используя склонность, можно определить, является ли функция возрастающей или убывающей в данной точке, а также найти точки экстремума и точки перегиба.

Кроме того, в алгебре и анализе склонность может быть использована для решения задач оптимизации. Например, при оптимизации функции требуется найти максимальное или минимальное значение функции. Зная склонность функции, можно найти точку, в которой производная равна нулю, что помогает найти точку максимума или минимума.

Применение в алгебреПрименение в анализе

Определение наклона прямой	Нахождение производной функции
Определение тангенса угла наклона прямой	Определение возрастания/убывания функции
—	Нахождение точек экстремума и точек перегиба
—	Решение задач оптимизации

Применение в геометрии и физике

Понятие slope, или наклон, широко применяется в геометрии и физике для описания и анализа различных явлений и объектов.

В геометрии slope используется для определения наклона прямой. Он показывает, как быстро прямая изменяется по вертикали в сравнении с изменением по горизонтали. Наклон прямой может быть положительным, отрицательным или равным нулю, что указывает на то, направленность прямой вверх, вниз или горизонтальную плоскость соответственно.

В физике slope применяется для анализа графиков, которые представляют зависимость одной величины от другой. Например, наклон графика скорости от времени позволяет определить ускорение тела. Также, наклон графика силы от длины пружины позволяет определить коэффициент упругости пружины.

Другим примером применения slope в физике является определение угла наклона поверхности. Наклон поверхности определяет ее геометрические свойства и может быть использован для решения задач в механике, оптике и других физических дисциплинах.

Таким образом, понятие slope играет важную роль в геометрии и физике, позволяя анализировать и описывать различные явления и объекты с помощью математических методов.

Свойства и особенности slope

СвойствоОписание

Значение slope	Slope представляет собой отношение изменения зависимой переменной к изменению независимой переменной.
Интерпретация slope	Значение slope может быть интерпретировано как скорость изменения зависимой переменной относительно независимой переменной.
Положительный и отрицательный slope	Если slope положительный, это означает, что зависимая переменная увеличивается при увеличении независимой переменной. Если slope отрицательный, это означает, что зависимая переменная уменьшается при увеличении независимой переменной.
Нулевой slope	Если slope равен нулю, это означает, что изменение независимой переменной не влияет на изменение зависимой переменной.
Бесконечный slope	Если slope является бесконечным, это означает, что зависимая переменная неограниченно возрастает или убывает в зависимости от независимой переменной.

Это лишь некоторые из свойств и особенностей slope. Понимание этих свойств поможет в анализе и интерпретации данных в различных областях науки и экономики.

Интересные факты о slope

2. Он обозначает наклон или склон поверхности, прямой или графика функции.

3. В математике slope обычно измеряется в виде отношения изменения y к изменению x.

4. Значение slope может быть положительным, отрицательным или нулевым, в зависимости от направления и величины наклона.

5. Если slope положителен, это означает, что функция или прямая имеет возрастающий наклон.

6. Если slope отрицателен, это означает, что функция или прямая имеет убывающий наклон.

7. Если slope равен нулю, это означает, что функция или прямая являются горизонтальными или параллельными оси x.

8. Знание slope позволяет анализировать графики функций, определять их поведение и свойства.

9. В геометрии, slope используется для вычисления углов наклона, векторов и градиентов.

10. Изучение slope помогает понять изменение одной величины относительно другой в различных математических моделях и приложениях.

Примеры решения задач с использованием slope

Вот несколько примеров задач, которые могут быть решены с использованием понятия slope:

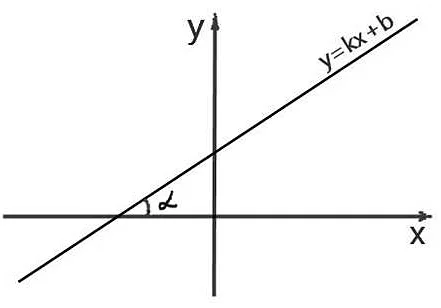
1. 1. Задача 1: Найдите slope прямой с уравнением y = 2x + 3 и определите наклон этой прямой.

Для решения этой задачи нужно заметить, что уравнение данной прямой имеет форму y = mx + b, где m — это slope. В данном случае, slope равен 2. Это означает, что прямая имеет наклон вверх и двигается вверх на 2 единицы по вертикали при каждом движении вправо на 1 единицу по горизонтали.

1. 1. Задача 2: Две точки (3, 5) и (7, 9) лежат на прямой. Найдите slope этой прямой.

Для решения этой задачи можно использовать формулу slope, которая выглядит так:

slope = (y2 — y1) / (x2 — x1), где (x1, y1) и (x2, y2) — координаты двух точек на прямой.

Подставляя значения из задачи в эту формулу, получим:

slope = (9 — 5) / (7 — 3) = 4 / 4 = 1.

Таким образом, slope этой прямой равен 1.

1. 1. Задача 3: Найдите slope прямой, параллельной прямой с уравнением y = -2x + 4 и проходящей через точку (2, 6).

Для решения этой задачи нужно знать, что прямые, параллельные друг другу, имеют одинаковый slope. Исходя из этого, мы можем использовать slope исходной прямой для нахождения slope искомой прямой. В данном случае, slope исходной прямой равен -2. Подставляя этот slope в формулу slope искомой прямой, получим:

slope = -2.

Таким образом, slope искомой прямой также равен -2.

Вопрос-ответ:

Что такое slope в математике?

Slope в математике — это показатель, который описывает скорость изменения одной величины относительно другой. Он также называется угловым коэффициентом и представляет собой отношение изменения по оси y к изменению по оси x на графике.

Как вычислить slope между двумя точками?

Для вычисления slope между двумя точками (x1, y1) и (x2, y2) нужно использовать формулу: slope = (y2 — y1) / (x2 — x1). Это дает нам значение скорости изменения между этими двумя точками на графике.

Какая интерпретация slope в математике?

Интерпретация slope зависит от контекста, в котором она используется. В геометрии, slope может быть интерпретирована как тангенс угла наклона линии. В физике, slope может представлять скорость изменения величины со временем. В экономике, slope может означать изменение спроса или предложения.

В каких областях применяется slope?

Slope широко используется в различных областях, включая геометрию, физику, экономику, статистику и инженерию. В геометрии, slope помогает определить наклон и угол линии. В физике, slope используется для измерения скорости изменения физических величин. В экономике, slope используется для анализа спроса и предложения. В статистике, slope используется для построения линейной регрессии и определения зависимости между переменными. В инженерии, slope используется для проектирования и оптимизации различных систем и процессов.